叙述性偏好法实验的有效样本量模型框架

朱 玮, 杨嘉智

(同济大学 建筑与城市规划学院，上海 20092)

叙述性偏好法(stated preference, SP)是指通过实验设计(design of experiment)，让被试者面对虚拟对象表达其偏好的一种调查和研究方法.相对于直接观察人们实际选择行为的显示性偏好法(revealed preference, RP)而言，SP具有变量变异性可控、相关性可控、被试行为可控、可加入实际中尚不存在的新变量或新产品等优势，有利于得到更加符合理论的数据和模型[1]，因此成为诸多研究和应用领域的常用方法.

应用SP法的一个关键步骤就是实验设计.通常研究者首先设定影响决策和选择的要素，并设定每个要素的水平；再组合不同要素的水平来生成选项，将若干选项组合成选择题供被试者选择；最后多采用离散选择模型方法(discrete choice models)[2-3]，通过解读模型估计的参数来推断偏好.因此，参数估计的可靠性和准确性至关重要.可靠性是指估计参数的离散程度，离散程度越小说明在重复试验中越不可能出现与估计值相差较大的参数值；准确性是指估计参数与真实参数的接近程度，越接近说明模型越能反映人们的真实偏好.两者往往随样本量的增加而提高.

但受成本限制，实际的调查实施总希望用尽量少的样本来得到足够可靠和准确的模型结果，称其为有效样本量.这需要采用一定的实验设计策略，常用的设计策略包括正交设计(orthogonal design)、效率设计(efficient design)[4-5]等，不同策略下的有效样本量可能不同.除此之外，影响有效样本量的还有要素的数量、水平的数量以及偏好本身的特征等因素.

目前关于SP实验设计样本量的研究主要集中在医学及商业决策等领域.运用较广的传统模型有Orme提出的经验法则(rule of thumb Ⅰ)[6]，指出样本量(被试人数)取决于选择题的数量、构成选择的要素数量，以及所有要素中出现的最大水平数量，它们之间的关系可以用简单的数学公式表示.之后Orme进一步指出在一般实验中，被调查人数至少在300人以上，结果才可能具有说服力(rule of thumb Ⅱ)[7].但两个经验法则都缺少充分的证明.另一个传统模型来自简单随机抽样理论(SRS theory)[1]，其样本量估算基于选择概率的真实值和估计值、每个被试者需要完成的任务数量，由公式可计算出有效被试者人数；不足的是，如果没有源于实际的调查背景便不能获得选择概率的真实值.文献[4-5]在简单随机抽样理论的基础上，提出了以协方差矩阵衡量实验设计效率的方法，以及利用参数检验得到最小样本量的实验设计策略(S-efficient design).

既有研究主要存在3点不足：①仅关注模型的可靠性，欠考虑模型的准确性.得到低标准误、统计显著的参数通常比得到接近真实值的参数容易，既有研究一般止步于此.在实证研究中，真实参数是未知的，成为准确性验证的主要障碍；②在有效样本量的影响要素中，未考虑偏好本身的特征.该特征具体来说就是偏好参数的尺度.根据离散选择模型的原理，大尺度的参数相较小尺度的参数更能减少随机误差的干扰，从而令选择结果的倾向更加明确，对偏好的估计相应更容易，因此所需的样本量理论上应更少；③有效样本量估计方法的可操作性、普适性低，一般需要针对特定问题预设参数值[4]，因此受预设过程本身可靠性的影响大，实施过程也比较复杂.

本文旨在弥补以上缺陷，得到一个更加容易操作的SP实验有效样本估计方法框架.具体来说，希望通过实施这一框架，得到一个(或几个，针对不同的设计策略)操作模型，应用该模型，便可以通过预设实验中要素的数量、水平的数量、偏好参数的尺度以及参数的目标准确度，来预估实验所需的有效样本量.

1 SP实验有效样本量估计方法框架

1.1 SP实验设计及选择模型概述

SP实验设计的一般过程为：①确定实验对象，根据其属性设定影响决策和选择的要素；②设定每个要素的水平；③采用选定的实验设计策略对不同要素的水平进行组合，生成选项，将若干选项组合成选择题供被试者选择.

SP实验的选择行为数据通常用离散选择模型来解释，其中最基本的是多项逻辑特模型(multinomial logit model)，其假定人们在选择时，面对选项i=1,…,I，选择概率pi为

(1)

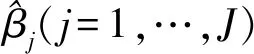
1.2 模型参数的准确性

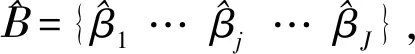
(2)

可见，该准确性与模型拟合参数的标准误成反比，与真实参数的容差成正比，如图1所示.从理论上可以推断，提高容差可以提高参数准确性，相应需要的有效样本量就会减少；相反，小容差就需要大样本.因此，容差尺度要适当，但又因具体应用问题而不同：参数误差造成的后果在多大程度上是可接受的，需具体情况具体确定.笔者将容差设定为0.1，即允许估计参数相对于真实参数有最多正负10%的偏移.

(3)

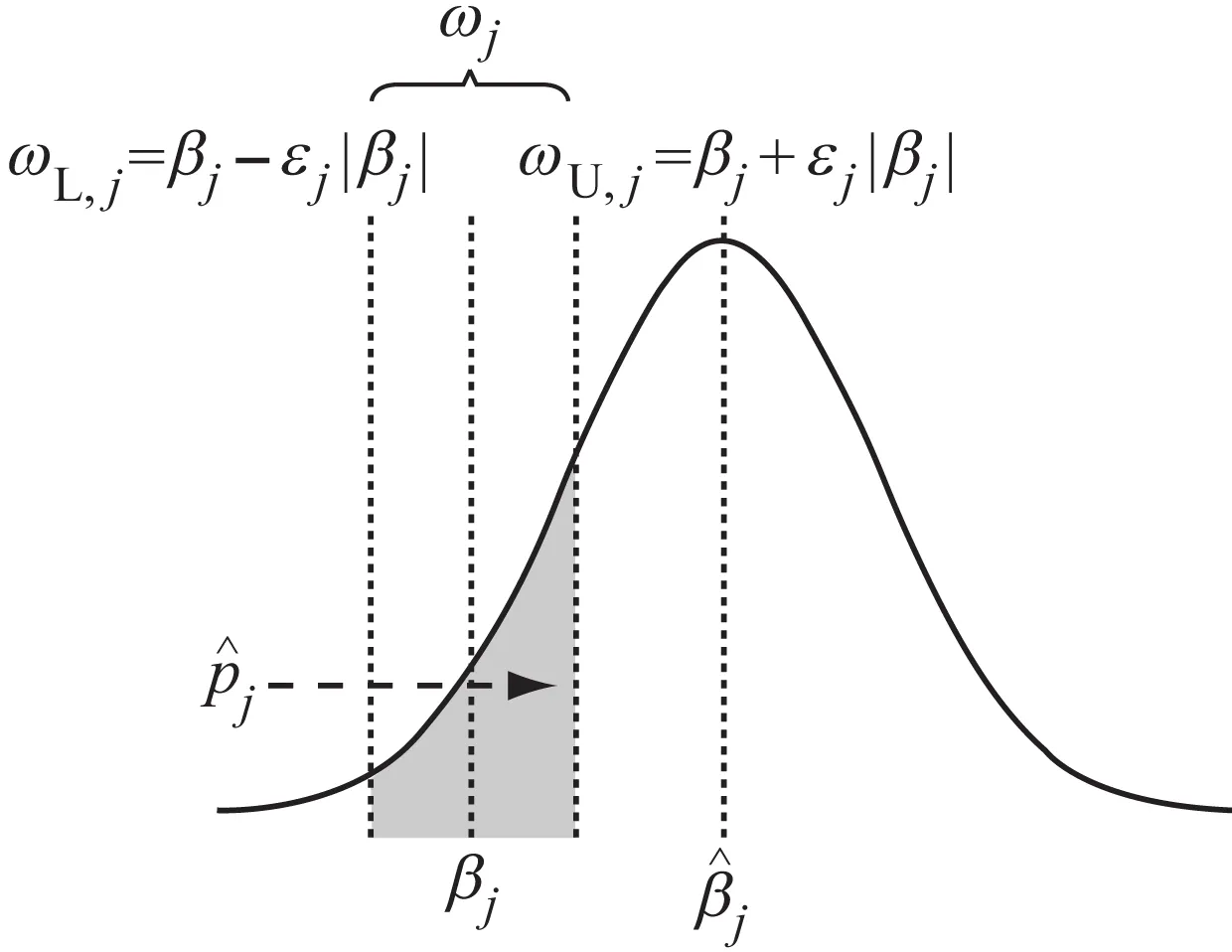
图1 参数准确性定义

1.3 准确性的影响因素模型

SP选择实验中，影响模型参数准确性的因素可能包括：① 样本量(xN).进入模型拟合的选择数量越多、选择结果越丰富，就能为模型提供越多的信息量，使得参数估计越准确；② 设计要素(解释变量)数量(xV)和要素水平数量(xL).这两个因素决定实验设计的复杂程度，要素和水平数量越多则生成选择方案的数量越多；相比于复杂度较低的实验设计，需要较大的样本量和较丰富的选择结果来得到相同准确性的参数估计；③ 模型参数的尺度(xS).参数尺度决定了可见效用相对于误差的作用强度,尺度越大则选择结果越确定，规律性越强，越容易得到准确的参数估计；④ 实验设计策略(xD).不同的实验设计策略(如正交设计、效率设计、随机设计)产生不同的选择方案，对应不同程度的信息丰富性和有偏性，从而影响参数估计的准确性.例如，正交设计可以产生具有代表性、均好性、数量较少的选择方案，但其自变量的信息量不随样本量的增加而变化；而随机设计在样本量较少时，自变量的分布很可能有偏，但随着样本量增加，有偏性会减弱，信息丰富性会增加.

以上影响因素与参数准确性的假设关系总结如表1所示.

表1 变量的含义及其与参数准确性的假设关系

Tab.1 Variables and hypothetical relationship with parameter accuracy

变量影响因素含义与参数准确性的假设关系xN样本量正相关(+)xV设计要素的数量负相关(-)xL设计要素水平的数量负相关(-)xS模型参数的尺度正相关(+)xD实验设计策略对应的选择方案丰富度正相关(+)

由于设计策略不易量化，因此在特定实验设计策略xD下，建构其余4个影响因素与参数准确性的关系模型，而设计策略的影响可通过比较不同设计策略对应模型的参数来获得.参数准确性的取值范围为0～1，通过预研究基本掌握了参数准确性在3个设计策略下(详见2.1)与样本量的关系，以要素数量、水平数量皆为3、模型参数尺度选择中类时为例(图2)，图中曲线接近标准逻辑斯蒂函数的上半部分(图3).

图2 参数准确性与样本量变化的关系(要素数量=3，水平数量=3，模型参数尺度=中类)

Fig.2 Parameter accuracy versus sample size

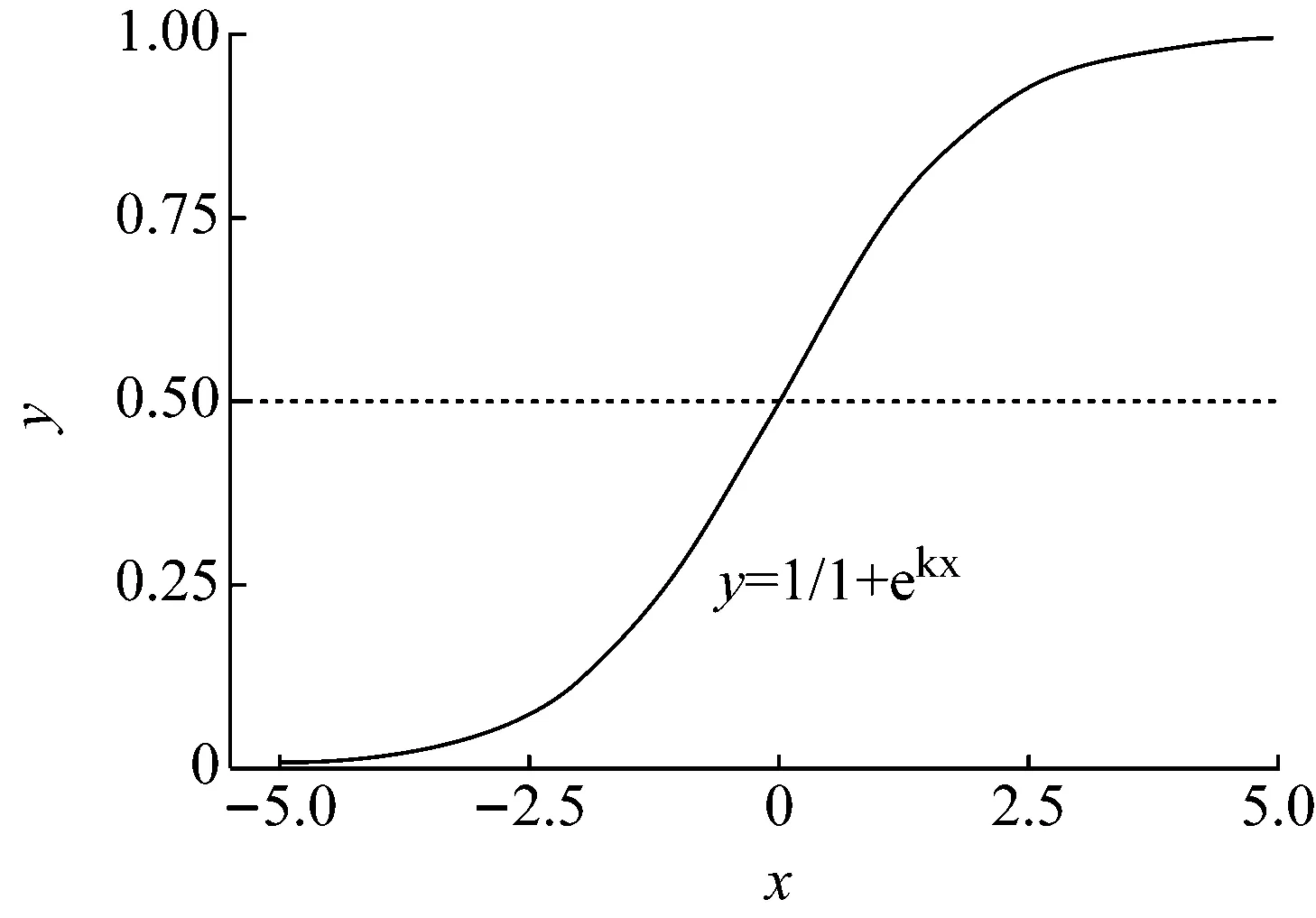
图3 逻辑斯蒂函数

标准逻辑斯蒂函数为

(4)

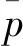
(5)

得

(6)

鉴于准确性的影响因素都要通过样本量起作用，例如当样本量为0，准确性也应为0；同时考虑到模型应较易于操作.因此，将自变量间的关系定义为如下乘积形式：

(7)

式中:βk为各影响因素xk的权重，可用线性回归模型求解.根据公式(7)，当给定实验设计策略、参数准确性、实验设计要素数量、要素水平数量以及参数尺度，即可求得实验所需的有效样本量.

2 有效样本量估计实证

本研究中的有效样本量是指得到足够模型参数准确性所需的最小样本量.应用以上的框架对SP实验的有效样本量进行实证研究.总体思路是，将以上5个参数准确性影响因素作为设计要素进行实验设计，得到不同的检验方案；根据每个方案，用模拟的方法生成虚拟决策数据，进行选择模型拟合，得到模型参数，并计算参数准确性.根据式(7)得到准确性的回归模型，考查影响因素与准确性的实证关系，以及不同条件下有效样本量的变化规律.

2.1 检验方案设计

对5个影响因素的等级设定如下：

(1) 设计要素的数量(xV)，为2～10个.

(2) 要素水平的数量(xL)，为2～4个.

(3) 模型参数的尺度(xS)，即为预设的真实参数，为大、中、小3个等级.大尺度参数值为0、2、4、8，中尺度参数值为0、1、2、4，小尺度参数值为0、0.5、1、2.

采用R语言的DoE.base包，对以上3个因素经过正交设计，得到27个检验方案，其中典型方案如表2所示.

(4) 样本量(xN)，根据每个检验方案以及对应选择方案规模，并根据式(1)，模拟2选1选择的若干样本.在每种策略下模拟了500、800、1 500、3 000、6 000、12 000、20 000、30 000次选择.

(5) 实验设计策略(xD)，选取了3种实验设计策略分别进行检验.一是将要素的数量扩大选项数两倍后做正交设计(偏移成对正交设计，shifted-pairs orthogonal design[8-9])，直接生成选择方案，以下简称“成对组合策略”；二是运用正交设计生成单个选项后，从中随机抽取两个选项组合成选择方案，以下简称“随机组合策略”；三是所有选项的要素值均随机生成，以下简称“完全随机策略”.一般来说，成对组合策略生成的选择方案最少，在小样本下的代表性和均匀性最好；完全随机策略的方案丰富性最高，利于降低参数偏差，但需要大样本才能得以体现；随机组合策略的特性居于以上两者之间.

表2 检验方案示例

2.2 准确性模型结果

分别在以上3种设计策略下实施检验方案，用R语言中的mlogit包拟合选择模型(式(1))，得到模型估计参数，根据式(2)、(3)计算该方案、该样本的模型参数准确性；接着用准确性模型对所有检验方案的所有样本加以回归分析，可得到3个对应设计策略的模型.根据式(7)，对准确性模型加以调整，主要是因为模型参数尺度因素(xS)在本实证中不易量化，进而采取哑变量的形式(0/1)，分别由xS1(小尺度)、xS2(中尺度)和xS3(大尺度)来表示；对应参数为βS1、βS2、βS3.式(7)相应调整为

(8)

在准确性模型拟合前，筛选准确性在0.70～0.95的样本予以保留，目的一是对准确性较高的样本建模更具针对性和实用性，二是去除异常情况.模型拟合结果见表3.

3种策略下模型参数的符号和关系均符合假设：参数尺度与准确性正相关；设计要素的数量和要素水平的数量均与准确性负相关，且要素水平的作用更强；样本数量与准确性正相关.模型中未加入常数项，因为常数项与xSc的作用重叠.将通过模型(式(8))估计的样本量与实际的样本量进行比较(图4).相比前两种策略，完全随机策略图像上的点分布更聚集，估计样本量与实际样本量更为接近，对两者的线性回归亦可同样证明.

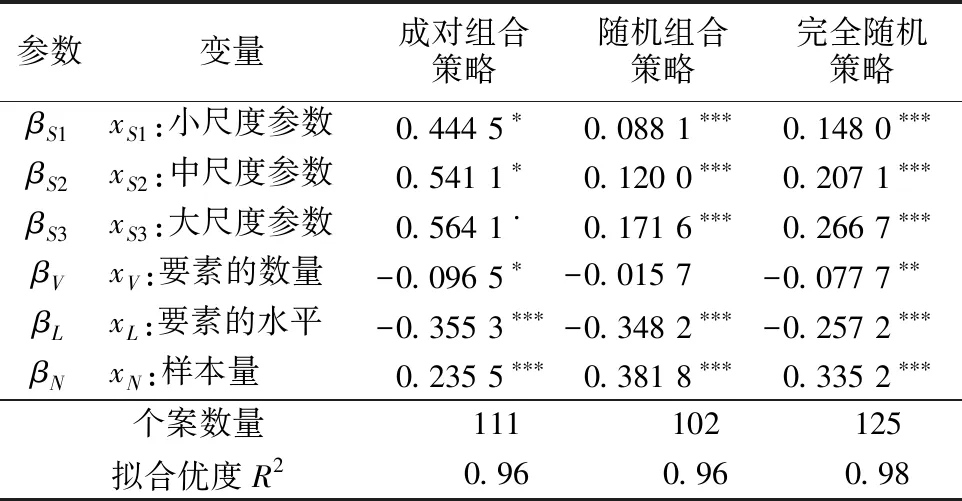
表3 准确性模型结果

注:***、**、*和·的统计显著性水平分别为0.001、0.01、0.05、0.1.

a 成对组合策略

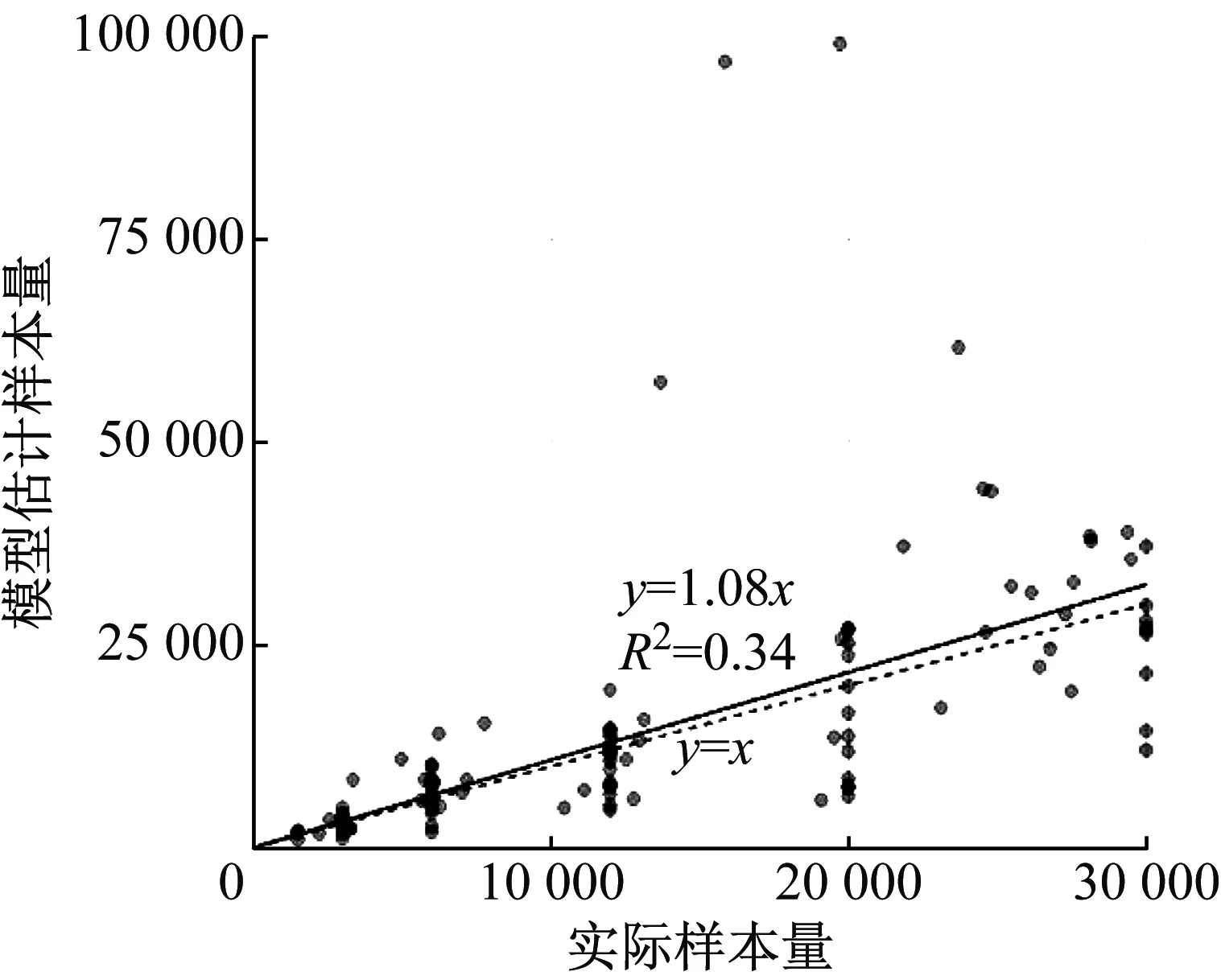
b 随机组合策略

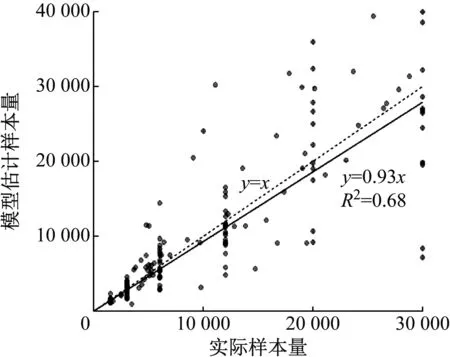
c 完全随机策略

2.3 有效样本量与影响因素关系的可视化

为了更加清晰地呈现有效样本量与其影响因素的关系，并便于对这3种设计策略进行比较，对以上模型进行可视化处理，如图5所示.图中，纵坐标表示27种要素与水平的组合，自下而上根据要素和水平的数量排列，越往上，选择的复杂性越高；横坐标表示在之前条件设定下估算的有效样本量.它们显示的规律是：① 要素数量和水平数量越多，需要的有效样本量越大，且要素水平数量的影响比要素数量的影响大得多.② 参数尺度越小，需要的有效样本量越大，且呈非线性增长，即从中尺度到小尺度参数需要增加的有效样本量比从大尺度到中尺度需要增加的有效样本量多得多.③ 参数准确性越高，需要的有效样本量越大，也呈非线性增长，即同等程度的准确性提高，在较高准确性下要比较低准确性下需要更多的有效样本量.④ 两种随机设计策略所需的有效样本量明显少于成对设计策略的样本量.例如，在最高的准确性、最小的参数尺度、最高的复杂性下，随机策略的有效样本量不超过40 000次选择，而成对设计策略需要超过60 000次选择.在参数准确性较低或在复杂度较低的条件下，成对设计策略需要的样本量与随机策略接近甚至更少.⑤ 比较这两种随机策略，完全随机策略在大多数条件下需要较少的有效样本量；仅在最高准确性、最小参数尺度、较高复杂性下，有效样本量略多于随机组合策略所需有效样本量.

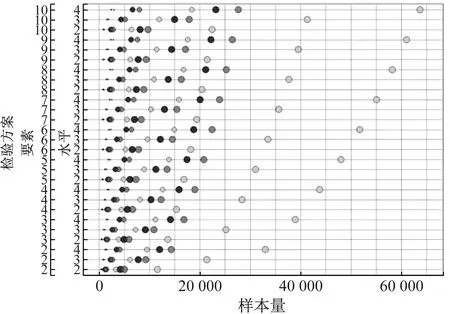
a 成对组合策略

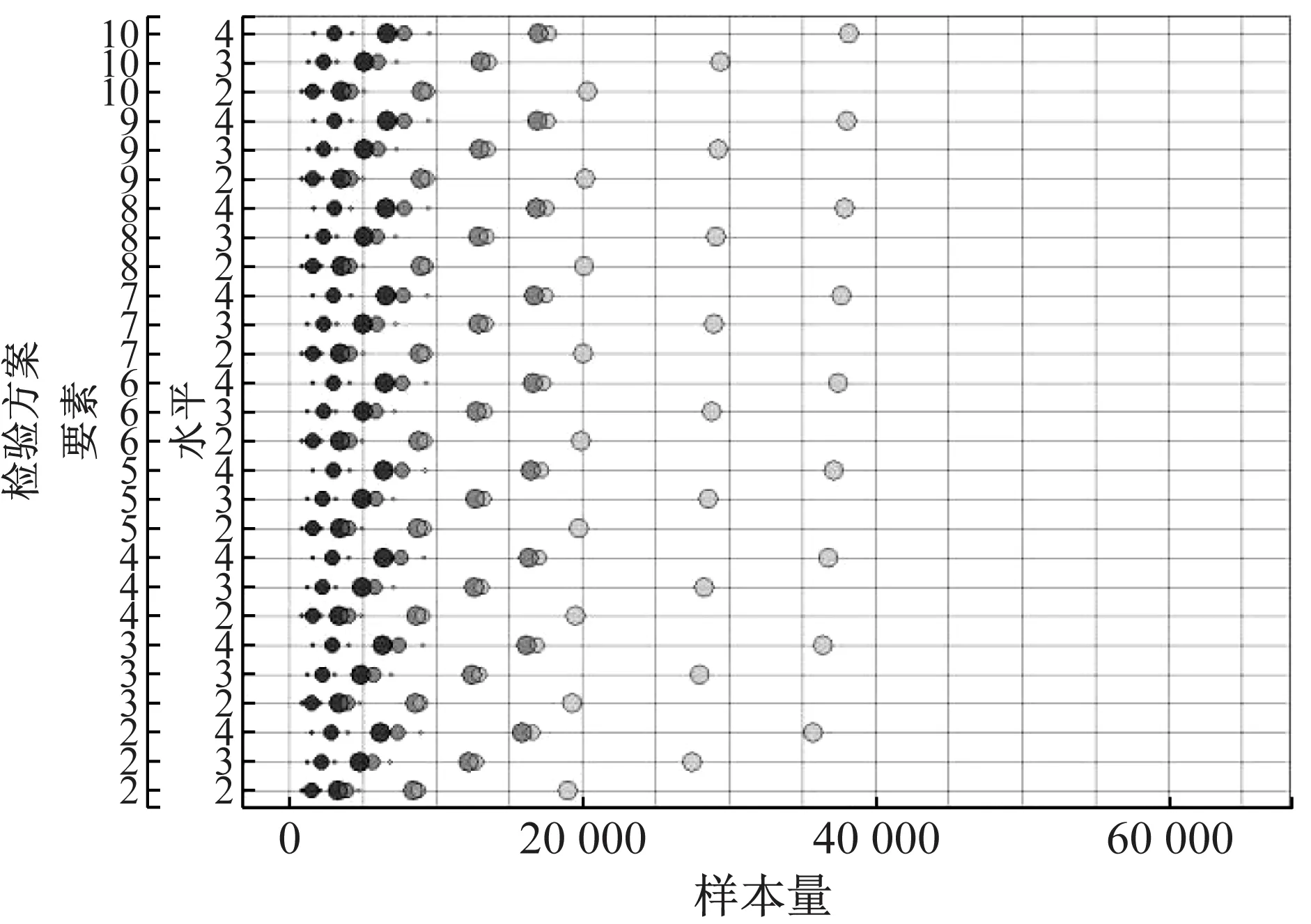
b 随机组合策略

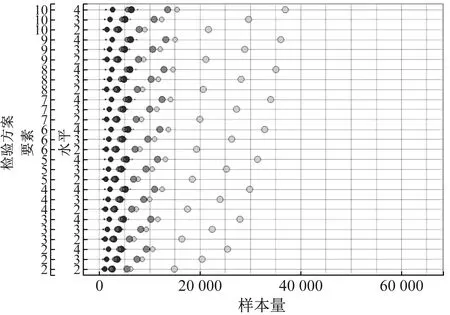
c 完全随机策略

3 结论

既有SP实验设计研究主要关注估计可信度高的参数，却忽略了对参数准确性的要求.对此，本文提出了一个以获得准确参数估计为目标，估计SP实验设计所需有效样本量的模型框架.研究的主要结论为：

(1) 提出了一个易于操作、更加全面的SP实验有效样本量估计方法框架，最终可通过一个线性模型来估计实验所需的样本量.该模型中的因变量为参数的准确性，解释变量包括要素的数量、要素水平的数量、参数的尺度、样本量以及实验设计策略.当预设包括准确性在内的其他变量，即可应用此模型求得有效样本量.

(2) 应用该框架开展了一个模拟检验，发现所有这些解释变量都对参数的准确性产生显著的影响，从中得到对SP实验设计的一些实践原则.第一，要素水平的数量比要素的数量更显著地影响样本量，因此实验应尽量控制要素水平数；第二，在估计样本量前，可通过预实验或文献查阅对参数尺度有所预估；第三，在高参数准确性的要求下，随机实验策略基本上要优于成对设计策略，仅在低参数准确性、大尺度参数等宽松的条件下，成对设计策略才体现出优势.

以上框架适用于基于SP选择实验的研究，帮助研究者评价实验设计，选择恰当的实验设计策略，预估样本量和实施难度.相信通过以上模拟检验得到的实验设计要素与有效样本量之间的关系在其他一般实验情景中仍是有效的，不过具体的关联程度应该会随着研究问题的不同而有所不同，因此仍需要具体问题具体研究.在这个过程中，比较难的步骤就是界定真实参数的尺度，因其对有效样本量规模有较大影响.通过预实验或文献查阅对参数尺度有较为准确的预估是需认真对待的环节.本研究也仅考查了影响有效样本量的部分因素，在此框架下，值得研究的要素还包括其他设计策略(如效率设计)和选项数量.此外，要素影响有效样本量的机制、模型是否还有其他更加贴切的形式，也值得深入探索，毕竟本研究模型还原实际样本量的准确度不高，其中有随机过程的影响.