龙卷风风场的数值模拟研究

王蒙恩， 曹曙阳， 操金鑫

(1. 同济大学 土木工程学院， 上海 200092； 2. 同济大学 土木工程防灾国家重点实验室， 上海 200092)

联合国防灾署的统计资料表明我国是世界上自然灾害经济损失最严重的3个国家之一，风灾因发生频率高且影响范围大成为防灾减灾工作的重点对象之一[1].龙卷风的机理区别于常规直线型大气边界层强风，具有旋转剧烈、突发性强、风速变化剧烈等特点，表现出强烈的三维流场特性.相对于其他风致灾害，龙卷风的发生将会导致更加严重的风灾.近年来，在我国东部和南部地区出现过多次较为严重的龙卷风事件，导致众多低矮民居、输电线塔和工业厂房等发生较为严重的破坏甚至倒塌[2].因此，有必要明确龙卷风的近地面风场结构，并在重要建筑结构的抗风设计考虑龙卷风的荷载效应.

自20世纪90年代始，移动多普勒雷达被广泛运用于监测龙卷风.1998年5月30日，美国南达科他州发生了至少两起强龙卷风，其中经过Spencer的一起龙卷风经DOW(doppler on wheels)移动雷达观测得到了珍贵的风速数据，龙卷风中心非常靠近DOW-3观测点[3].但由于实测龙卷风风险较大，机会极少，且雷达无法准确观测到近地面的风场数据[4]，因而目前的研究多以物理试验研究和数值模拟研究为主.

Ying等[5]建立了世界上第一台可用于龙卷风旋涡模拟的设备，并研究了龙卷风旋涡内的切向速度和径向速度的剖面.基于Ying等[5]的理念，Ward[6]在模拟器顶部安装了控制风机来产生上升气流，开发出了应用最广的Ward型龙卷风模拟装置，此模拟器考虑了径向入流与切向环流的比例引起的龙卷风单涡结构变化，并预测了多涡结构的可能，较好地重现了实际龙卷风的结构.基于Ward型模拟系统，较多学者开展了对龙卷风旋涡结构的物理试验研究[7-11].美国爱荷华州立大学的Haan等[12]基于Ward型模拟器的设计理念，将导流板设置在模拟器的顶部，利用排风扇产生上升气流，设计出一种新型龙卷风模拟器，该模拟器还能实现模拟现实中龙卷风的移动效应.Hangan等[13]研制了一种新型的三维风洞实验室WindEEE(wind engineering, energy and environment)Dome，该设备可用于模拟不同类型的风场，诸如龙卷风、下击暴流和阵风锋面等.为了研究龙卷风对桥梁、建筑结构的作用，同济大学也建立了新型龙卷风模拟器[14].该模拟器基于Haan等[12]的设计原理建造，可以方便地研究龙卷风风场特性以及对结构的荷载效应.

土木结构风荷载和效应的数值模拟及数值风洞是结构风工程研究中具有战略意义的发展方向，也是当前国际风工程研究的一个热点[15-16].Diamond等[17]通过数值模拟的方法研究了粗糙度对龙卷风涡结构的影响，发现粗糙度会加强风速但会减小涡流比.Lewellen等[18]采用大涡模拟方法研究了相关参数对龙卷风风场的影响，发现即使是相同涡流比的情况下，龙卷风涡结构特性也会因诸多参数的不同而不同，主要包括粗糙度、龙卷风移动速度、入流边界情况等.Lewellen等[19]通过数值模拟的方法研究了涡流比及粗糙度对风场的影响，发现增加入流会减小涡流比.Ishihara等[20]采用大涡模拟方法研究了龙卷风涡结构特性，其选用了Ward型龙卷风模拟器原型，并成功模拟出单涡及双涡类龙卷风涡结构.李雪[21]基于Ward型龙卷风模拟器的数值模型生成了与台风涡类似的涡结构.徐枫等[22]建立了龙卷风发生装置的数值计算模型，对具有单涡结构的龙卷风风场进行了研究.

本文采用数值模拟的研究手段，运用大涡模拟方法模拟了3种不同涡流比条件下的龙卷风风场结构.运用物理试验模拟数据和现场实测龙卷风风场数据验证了数值模拟的可行性.研究了龙卷风三维风场速度在不同方向上的分布、龙卷风风压分布、龙卷风涡核半径和龙卷风气流的脉动特性，探讨了涡流比对龙卷风风场的影响效应.

1 研究方法与数值模型

1.1 控制方程

大涡模拟首先在湍流控制方程中将小尺度涡滤掉，其次通过考虑附加应力项来再现湍流流场.本文运用开源计算软件OpenFOAM，采用大涡模拟方法，亚格子模型选用标准Smagorinsky模型，控制方程如下：

(1)

(2)

(3)

(4)

(5)

1.2 数值模型与边界条件

同济大学龙卷风模拟器是国内首个ISU(Iowa State University)型龙卷风模拟器，如图1所示.整个系统由3个同轴圆状筒构成，风机和导流板放置在模拟器顶部，这样气流经风机吸收，通过导流板和外围圆筒，在升降平台与蜂窝网间形成龙卷风涡旋.此类模拟器为回流式风洞，试验平台为开口式，可以更方便地研究龙卷风动力特性以及对结构的影响.

a 示意图

b 实体图

基于同济大学龙卷风模拟器，建立数值模型，如图2所示.数值模型尺寸与物理模拟器尺寸一致.

a 剖面图

b 三维图

数值计算模型网格划分如图3所示.在竖直方向，近地面风场特性为研究重点，因此在地面附近的网格最为精细，竖直方向网格尺寸以小于1.2的比例增加.在水平方向，涡核中心和涡核半径附近的流场特性也是研究重点，因此中心网格最为精细，水平方向网格也以小于1.2的比例增大，网格总数为120万左右.

边界条件设置见表1.其中，入口边界给定初速度，由轴向速度和切向速度组成.轴向速度v=1 m·s-1，切向速度不定，通过改变切向速度大小可得到不同的涡流比结果.上出口边界条件压力为定值0.

表1 边界条件设置汇总

注：出入口混合边界物理意义为当该边界的速度方向朝外时，速度定值为零；当该边界的速度方向朝内时，速度边界为零梯度.

a 三维图

b 主视图

c 底视图

1.3 求解格式

本文采用有限体积法进行计算，差分格式采用二阶中心差分，采用PIMPLE算法.计算到t=7 s时流场已经稳定.本文所有算例均取t=10～30 s时间间隔内的数据进行统计分析.

2 参数定义与试验工况

龙卷风风场特性受诸多因素的影响，主要有：涡流比、高宽比、径向雷诺数等.其中，涡流比是影响龙卷风风场特性最重要的参数[13]，随着涡流比的增大，流场从层流过渡为湍流，从单涡核结构过渡到双涡、多涡结构.涡流比的定义如下：

(6)

式中：Γ为环向流量；Q为单位时间内通过模拟器的气流流量；a为高宽比，a=H/r0；H为入流高度，本文设置为0.2 m；r0为上升气流半径，本文设置为0.25 m；R为模拟器入流半径，本文设置为0.625 m；Ut为平均切向速度；h为相对地面的高度.

径向雷诺数的定义如下：

(7)

式中：ν为空气运动黏度，取值为1.48×10-5m2·s-1.

本文主要研究了3种不同涡流比条件下的龙卷风风场特性.算例参数汇总如表2所示.表中，Ut max为流场中最大平均切向速度；hmax为Ut max发生处平面的高度；Rmax为Ut max发生处相对涡核中心的距离，即hmax高度处的涡核半径.

表2 数值模拟算例参数

3 计算结果分析

3.1 数值模拟结果验证

将数值模拟结果与物理试验结果和现场实测结果进行对比分析，以验证数值模拟的可行性.龙卷风风场可以用三维速度和气压降进行描述.三维速度分量中切向速度为最主要的分量，气压降往往是造成结构破坏的最主要因素.因此，数值结果的验证主要针对切向速度分量和气压降进行分析.

图4为h=0.5hmax高度平面的数值模拟龙卷风切向速度沿径向的分布(S=0.235,S=0.546和S=0.768)与物理试验结果[23](S=0.74)、现场实测结果[13](Spencer龙卷风和Muhalll龙卷风)和理论模型[24](Rankine模型和Burgers-Rott模型)的对比.其中，r为相对涡核中心的距离.图中纵、横坐标分别基于当前高度平面的最大切向速度(Ut max,h)和对应的涡核半径(Rmax,h)进行了量纲一化处理.图示表明，通过数值模拟得到的龙卷风切向速度分布与通过物理试验以及现场实测得到的结果具有一定的一致性.

图4 量纲一化平均切向速度沿径向分布的对比

图5为不同研究方法之间关于风压分布的对比.其中，p为平均风压，|pmin|为流场平均风压绝对值的最大值，r0.5pmin为0.5倍pmin发生位置相对涡核中心的距离.根据Karstens等[25]的现场实测结果，Webb龙卷风的涡核形态不明确，Tipton龙卷风为双涡核龙卷风.根据图5a，数值模拟低涡流比(S=0.235)工况的计算结果和物理试验[23](S=0.23)的研究结果、Webb龙卷风实测数据吻合较好.根据图5b，数值模拟高涡流比(S=0.546)工况的计算结果和物理试验[23](S=0.52)的研究结果、Tipton龙卷风实测数据吻合较好.

a S=0.235

b S=0.546

通过以上关于切向速度分布和气压降分布的对比分析，验证了数值模拟龙卷风的可行性.

3.2 流场平均特性

图6给出了量纲一化平均切向速度沿径向的分布.其中纵、横坐标分别对Ut max和Rmax进行了量纲一化处理.可以发现，不同高度平面的切向速度分布形式存在差异.在涡核半径内部，高度越高，切向速度增长率越小；在涡核半径外部，高度越高，切向速度衰减率越小.随着高度的增加，涡核半径逐渐变大，不同高度平面内最大切向速度先增大后减小.不同涡流比条件下的平均切向速度分布大致相同.

a S=0.235

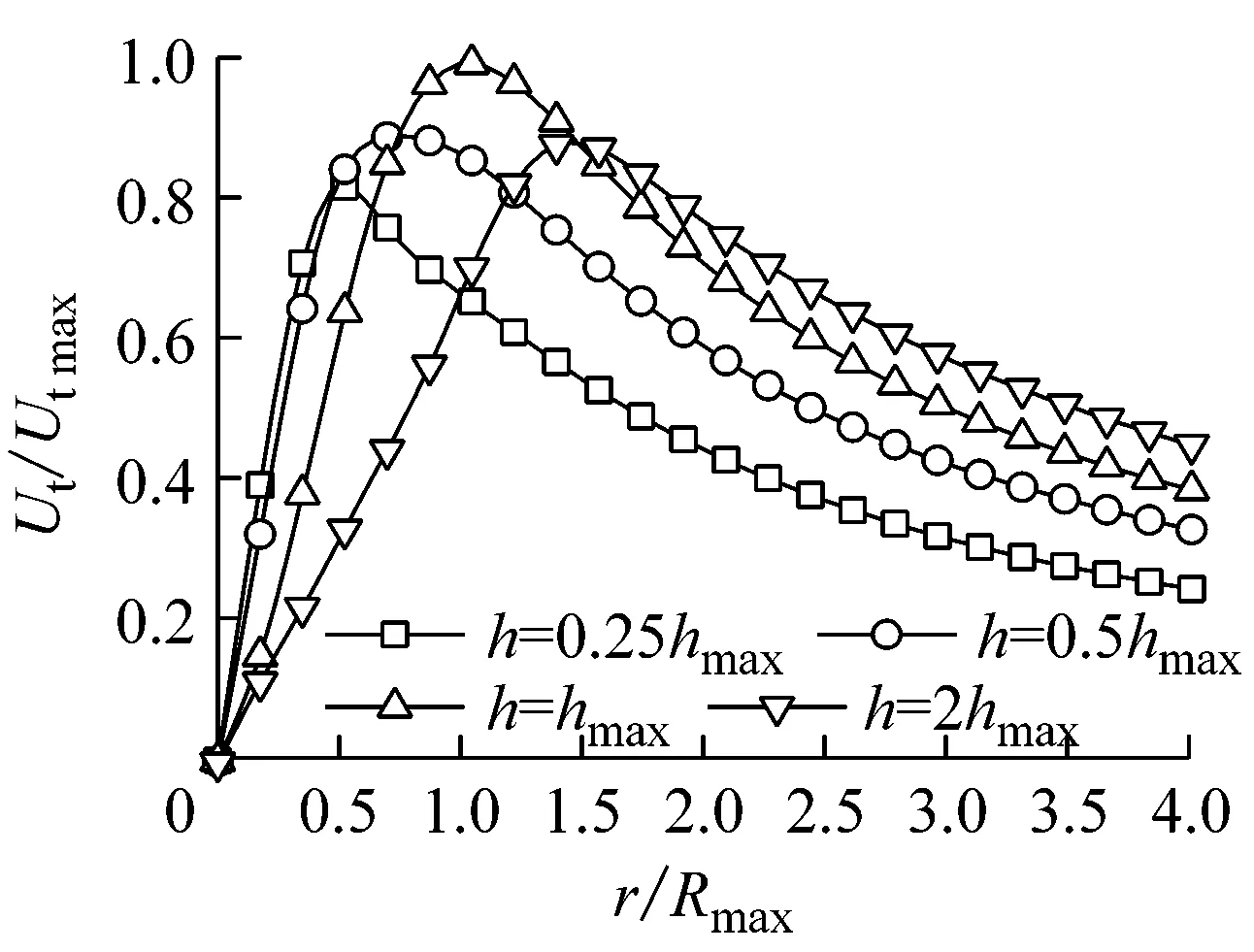
b S=0.546

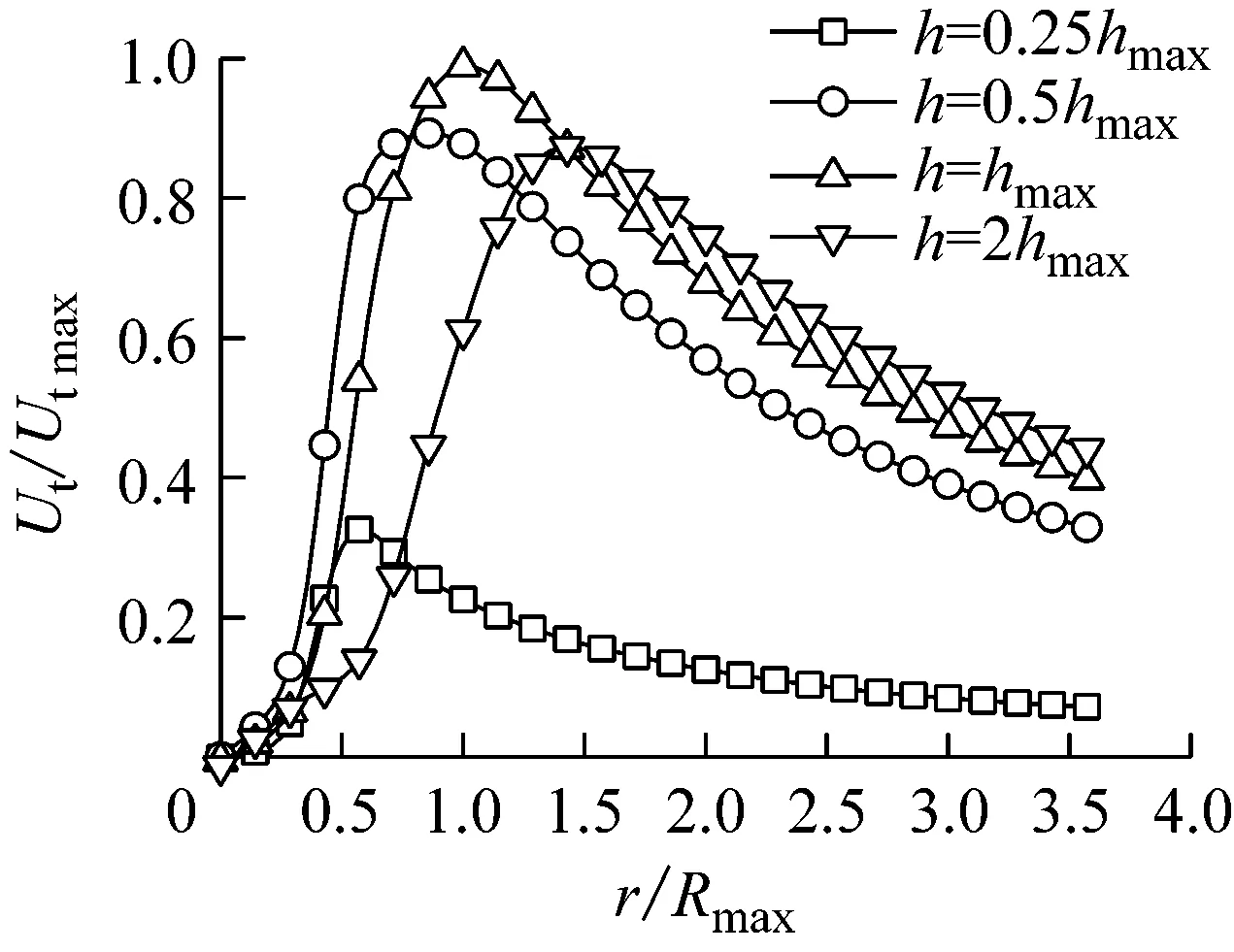
c S=0.768

Fig.6 Normalized mean tangential velocity as a function of radial distance at different heights

图7给出了量纲一化平均切向速度沿轴向的分布.低涡流比(S=0.235)条件下，涡核半径内外的切向速度分布与大气边界层风剖面接近.高涡流比(S=0.546、S=0.768)条件下，涡核半径内部包括涡核半径位置，切向速度的轴向剖面均呈现一定的速度剪切特性，即最大切向速度发生在近地面高度，该现象与大气边界层风剖面存在较大差异.涡核半径外部，切向速度剖面与大气边界层风剖面较为接近.

a S=0.235

b S=0.546

c S=0.768

Fig.7 Normalized mean tangential velocity as a function of axial distance at different radial locations

图8为量纲一化平均径向速度沿径向的分布情况.其中，Ur为平均径向速度.低涡流比S=0.235工况下，径向速度全为负，且沿径向变化较小，说明龙卷风气流全部向涡核中心汇集.结合图9，随着高度的增加，径向速度先增大后减小，最大径向速度发生在近地面，达到0.5Ut max.涡流比S=0.546工况下，近地面高度的径向速度沿径向先增大后减小，较高处，径向速度出现正值，说明龙卷风气流在较高处出现向外流的现象；沿高度方向，如图9b所示，涡核半径处径向速度先沿负向增至最大,随后沿正向增至最大.涡流比S=0.768工况的径向速度分布与S=0.546工况类似，但涡核中心附近径向速度减小.

图8 不同高度量纲一化平均径向速度沿径向分布

Fig.8 Normalized mean radial velocity as a function of radial distance at different heights

图9 不同径向位置量纲一化平均径向速度沿轴向分布

图10为量纲一化平均轴向速度沿径向的分布.其中，Uv为平均轴向速度.涡流比S=0.235条件下，轴向速度在涡核中心附近出现最大值，随着与涡核中心的距离加大，轴向速度逐渐减小.且从图11a可以发现，轴向速度沿轴向在涡核中心附近先增大后减小，远离涡核中心处，轴向速度较小.涡流比S=0.546条件下，轴向速度在涡核中心附近出现负值，说明龙卷风气流出现向下的流动，沿着径向，不同高度处的轴向速度在0.5Rmax附近出现极大值.在S=0.768工况下，近地面高度(h=0.25hmax)和涡核中心附近(r=0.25Rmax)，轴向速度接近于0.

图10 不同高度量纲一化平均轴向速度沿径向分布

龙卷风中心极强的负压是导致建筑结构破坏的重要原因之一.图12为不同涡流比条件下风压沿径向的分布.其中,纵坐标为数值计算得到的平均压力p减去入口边界的平均压力pref.在S=0.235工况下，涡核中心出现负压极值.在S=0.546工况下，负压在涡核中心附近未出现明显的极值，但涡核中心气压降有较大幅度增大.涡流比S=0.768工况相比S=0.546工况，涡核中心气压降减小，负压在涡核中心两侧分别出现极值，说明龙卷风的单涡结构可能发生破碎，逐渐发展成双涡核结构.

图11 不同径向位置量纲一化平均轴向速度沿轴向的分布

Fig.11 Normalized mean axial velocity as a function of axial distance at different radial locations

图12 不同涡流比工况平均风压沿径向的分布

涡核半径是表述龙卷风尺寸的一个重要参数.图13为不同高度平面涡核半径(Rmax,h)随涡流比的改变.可以发现，涡核半径在不同高度平面均随涡流比的增大而增大.龙卷风的涡核半径随着高度的增高而增大，但在不同涡流比条件下的增大趋势不同.

3.3 流场脉动特性

龙卷风气流在涡核内部表现出较强的脉动特性.图14为切向速度标准差沿径向的分布.其中，Ut,std为切向速度标准差.涡流比S=0.235条件下，涡核中心处Ut,std最大，近地面高度的Ut,std大于较高高度处.涡流比S=0.546和S=0.768条件下，Ut,std减小，极值点偏离了涡核中心.图15为用测量点平均切向速度Ut,loc量纲一化处理的切向速度标准差沿轴向的分布.量纲一化切向速度标准差随着远离涡核中心而逐渐减小.随着涡流比的提高，切向速度脉动最大的点出现在最大切向速度发生的高度附近.

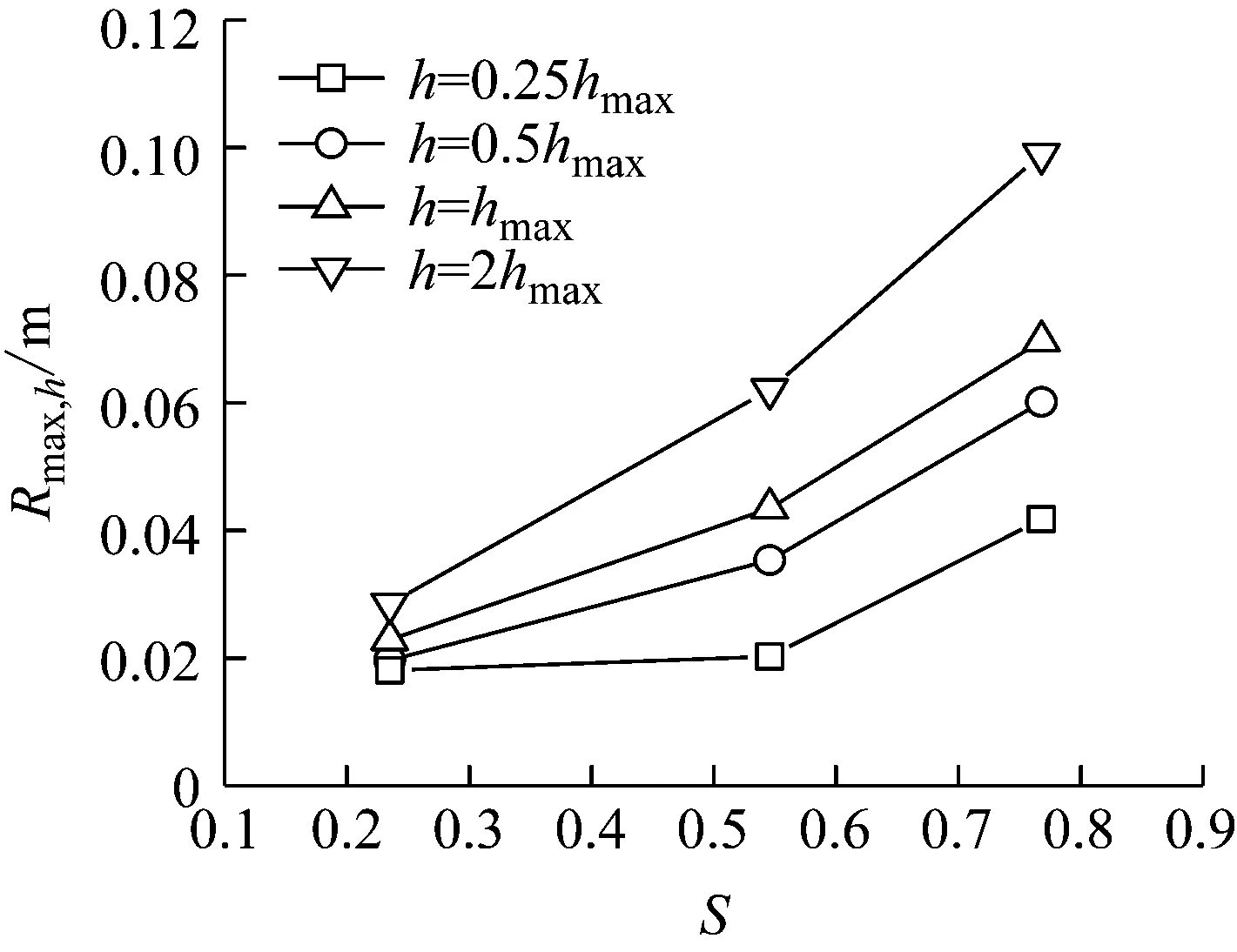
图13 不同高度涡核半径随涡流比的改变

Fig.13Vortex core radius as a function of swirl ratio at different heights

图14 不同高度切向速度标准差沿径向的分布

Fig.14 Standard deviation of tangential velocity as a function of radial distance at different heights

图16为量纲一化处理的风压标准差沿径向的分布.其中，σp为风压标准差.涡流比S=0.235条件下，风压标准差在涡核中心出现极大值，说明涡核中心附近压力脉动特性显著.随着涡流比的增大，涡核中心风压脉动特性减弱，但在涡核中心两侧出现新的极值.在涡流比S=0.768条件下，涡核中心两侧出现明显的极大值.说明，随着涡流比的增大，龙卷风单旋涡破碎，逐渐演变为双涡形态.

图15 不同径向位置量纲一化切向速度标准差沿轴向的分布

Fig.15Normalized standard deviation of tangential velocity as a function of axial distance at different radial locations

图16 不同涡流比工况量纲一化风压标准差沿径向的分布

Fig.16 Normalized standard deviation of wind pressures of different swirl ratio cases as a function of radial distance

4 结论

以同济大学龙卷风模拟器为原型，运用计算流体动力学方法构建了龙卷风风场的数值计算模型.通过与物理试验结果和实测结果的对比，验证了数值模拟的可行性.以涡流比为重点研究参数，探究了3个不同涡流比条件下的龙卷风风场结构.主要结论如下：

(1) 在涡核半径内，平均切向速度随着距涡核中心距离的增加逐渐增大；在涡核半径外，平均切向速度随着距离的增加而减小.随着涡流比的增大，龙卷风风场内的最大平均切向速度变大；涡核中心附近位置的平均切向速度轴向分布出现了明显的速度剪切现象.

(2) 随着涡流比的增大，4倍涡核半径范围内的平均径向速度出现了正值，平均轴向速度出现负值；即随着涡流比的增大，原来沿径向向内流动、沿轴向向上流动的龙卷风气流发生改变，出现了沿径向向外、沿轴向向下流动的现象.

(3) 龙卷风气流在涡核中心出现明显的气压降，随着涡流比增大，涡核中心负压极值先逐渐消失，而后在涡核中心两侧出现新的负压极值；涡核半径随着离地面高度的增大而逐渐变大，符合真实龙卷风旋涡的形态.

(4) 龙卷风涡核内部的速度和风压均表现出了强烈脉动特性.涡核中心附近切向速度脉动成分极大.随着涡流比增加，切向风速标准差极值点偏离原涡核中心.

(5) 随着龙卷风涡流比的增大，龙卷风单涡核结构发生破碎，逐渐发展为双涡核结构.