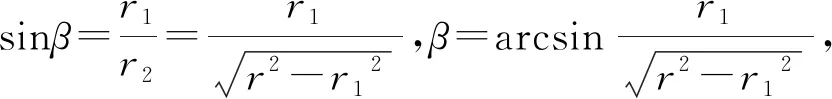圆形有界磁场“磁聚焦” 规律再探讨

廖香林

(四川省蓬安县周口中学,四川 南充 637000)

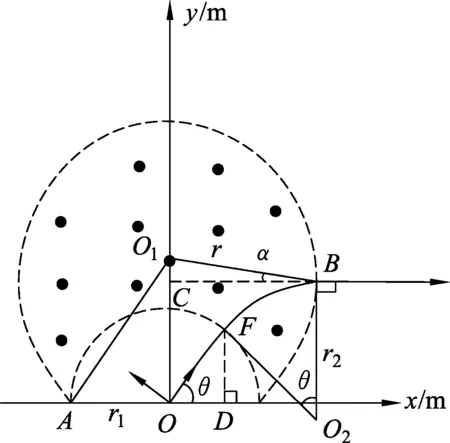
圆形有界磁场模型在历年高考试题和模拟题中反复出现,其中有很多试题都考查到一个重要的物理规律“磁聚焦”,即速率相等的同种带电粒子相互平行地射入圆形有界磁场后聚焦到圆上同一点;或者从圆上同一点沿不同方向发射速率相等的同种带电粒子最后相互平行射出磁场(如图1).当然要实现“磁聚焦”过程带电粒子的速度需要满足一定条件．该类考题多次出现,为了再挖掘探究“聚焦”规律,我们把原完整圆形磁场挖去部分区域并以一半圆向上凸起形成如图2所示的“月牙形”有界磁场,已知O点为半圆圆心,问:从O点沿不同方向发射进入磁场的带电粒子能否相互平行地射出?如能,其速度满足什么条件?下面我们重点探究这一问题以及相关规律．

1 “磁聚焦”基本规律探讨

为了方便，先简要探析完整有界圆形磁场“磁聚焦” 的条件,如图1所示从最低点沿不同方向发射的带负电粒子水平平行射出左边圆形边界而后聚焦在右边圆形边界最低点．带电粒子的入射速度满足何种条件?

图1

(1)

即满足条件r0=r的带电粒子做匀速圆周运动的半径等于圆形边界的半径,需要注意的是带电粒子做匀速圆周运动的半径由运动速度决定,因而(1)式更具有物理意义．

2 “磁聚焦” 规律再探讨

图2

现从半径为r圆形磁场挖去一部分区域并向上凸起半圆形成“月牙形”有界磁场,如图2所示,已知半圆半径为r1,且0≤r1

解析:可以先假想一个带电粒子从O点沿任意θ角方向发射最后水平向右射出,根据带电粒子在磁场中做匀速圆周运动特点以及几何关系可以得到一个含有θ数学表达式,如果满足合适的条件该表达式对于任意θ都成立,那么说明从O点以不同方向射入磁场的相同带正电粒子能相互平行射出有界磁场,而该“合适的条件”将是“月牙形”有界磁场“磁聚焦”的几何条件,最后再根据洛伦兹力提供向心力将几何条件转化为物理原理即速度满足的条件．

图3

r1cosθ+r2sinθ=rcosα.

(2)

(3)

由(2)、(3)两式消去α并整理得到

(4)

整理得

0.

(5)

(6)

(7)

带电粒子做匀速圆周运动的速度满足(7)式,则从O点以不同方向射入磁场的带电粒子能水平平行射出有界磁场,因而(7)式是“月牙形”有界磁场“磁聚焦”的物理条件．

特别注意:回归到基本的磁聚焦对应的条件小圆半径为0,即r1=0,聚焦点也由半圆的圆心蜕变为大圆的最低点．

根据图1可以看出从最低点发射的能进入磁场的所有带电粒子均能水平平行射出,而对于图3中的物理现象是否也遵循此规律?答案是否定的．如图4所示．设有一与水平向左成β角发射粒子恰好过边界最高点并向右射出．不难看出从小于β角射入磁场的带电粒子将从磁场左边界射出并不会水平向右平行射出.根据图3的证明过程可以看出从大于等于β角射入磁场的带电粒子将水平向右平行射出,因而要水平平行发射出去发射角度只能在一定范围内,下面计算临界角β.由几何关系结合(6)式可得

图4

总结:物理规律教学是物理教学的核心组成部分.我们不仅要注重物理规律所涉及物理量之间的最为本质的联系,更要注重规律成立和适用的条件范围,在教学中不仅要引导学生认识规律本身也要培养学生再思考、再认识、再探究物理规律的能力．如同本文把原本完整圆形有界磁场区域挖去部分区域形成“月牙形”有界磁场后,也能发生“磁聚焦”．只是满足的条件和聚焦点不同而已,但后者包含前者因而其意义更为广泛．

特别说明:本文所涉及的带电粒子只考虑受洛伦兹力作用,不考虑其它力的作用．另外“磁聚焦”与“磁发散”互为逆过程,本文不做区别,为了方便描述统一都用“磁聚焦”．