2019年4月浙江物理选考卷第20题的深度分析
张建斌 柴春琪
(1. 北京师范大学附属嘉兴南湖高级中学,北京 100087 2. 浙江嘉兴市第一中学,浙江 嘉兴 314001)
《普通高中物理课程标准》明确将科学论证作为科学思维的主要内容纳入物理学科核心素养.科学论证就是论证思维在自然科学领域的运用,其内涵是“利用证据建立科学的理由以支持科学主张”.科学论证取向下的高中物理教学就是将科学活动中的论证引入物理教学,引导学生像科学家一样开展基于证据的论证活动以发展学生的科学思维能力.
一个好的习题对于学生而言就是一个科学问题,犹如一个科学问题对于科学家而言就是一道习题一样.通过习题教学,使学生在科学思维、探究能力、实践意识、科学态度等方面得到有效提升.习题教学的作用不仅仅是为了得到答案,而是要全面提高学生的问题解决能力,发展包含科学论证在内的科学思维素养.现以浙江省2019年4月物理选考卷第20题为例,展开案例研究,以期为科学论证取向的物理习题教学提供实践性知识.
1 原题呈现与试题解析
例题.(2019年4月浙江省物理选考卷第20题)某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立如图1所示的物理模型.竖直平面内有一倾角为θ=37°的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似为0,但允许砂粒通过.转轮半径R=0.4 m、转轴间距L=2 m的传送带以恒定的线速度逆时针转动,转轮最低点离地面的高度H=2.2 m.现将一小物块放在距离传送带高h处静止释放,假设小物块从直轨道B端运动到传送带上的C点时,速度大小不变而方向变为水平方向.已知小物块与直轨道和传送带间的动摩擦因数均为μ=0.5(sin37°=0.6).
(1) 若h=2.4 m,求小物块到达B端时速度的大小;
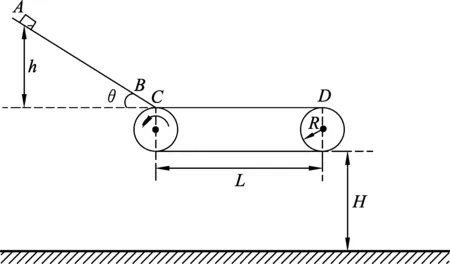
图1 原题示意图
(2) 若小物块落到传送带左侧地面,求h需要满足的条件;
(3) 改变小物块释放的高度h,小物块从传送带的D点水平向右抛出,求小物块落地点到D点水平距离x与h的关系式及h需要满足的条件.
参考答案: (1) 物块由静止释放到B的过程中
mgsinθ-μmgcosθ=ma.
vB=4 m/s.
(2) 左侧离开,D点速度为0时高为h1,
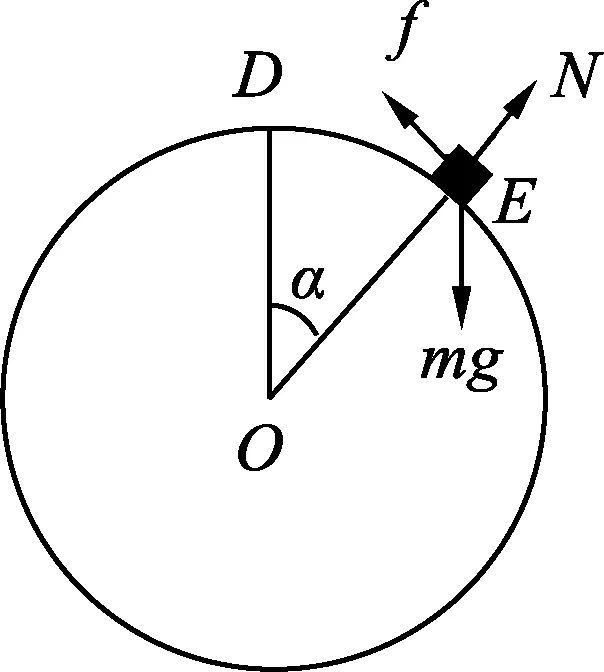
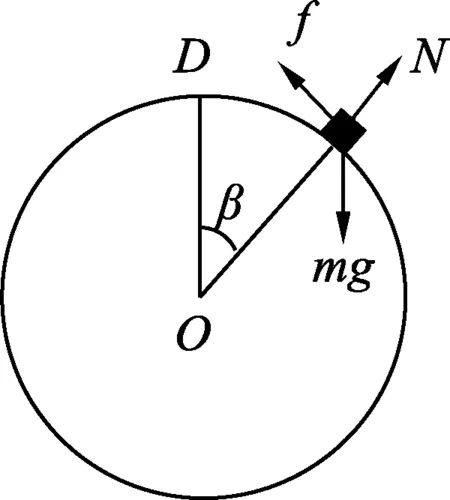
得h (3) 右侧抛出,D点的速度为v, 为使能在D点水平抛出, 得h≥3.6 m. 从提供的参考答案中可以看出,第(2)问认为物块能从传送带左端落下的临界条件是物块到达D点时的速度为0,然后将在传送带对其摩擦力的作用下向左运动,继而从左侧落到地面. 对比(1)中的“4 m/s”,参考答案给出的“3.0 m”多了一位有效数字,是否意味着这是采取“近似处理”得到的结果,而非严格意义的答案?如果真是这样,这第(2)问需要一定的勇气和解答策略,因为从严格意义上看,物块速度为0的临界点应在D点右下侧位置,但无法通过简单计算获得h的值,考生只能认为速度为0的临界点是D点,或是没有意识到这个问题而直接进行答题了.作为承担着“甄别和选拔学生”功能的试题,这样的设计是有欠考虑的.虽然试题的设计思路是考你会不会(相互割裂地设问,让你不会做),但试题应依据物理学科核心素养的“物理概念”、“科学思维”、“科学探究”、“科学态度与责任”4个方面及其水平,结合课程内容的要求,依据不同水平学业成就表现的关键特征而命制. 从这个层面而言,这是一道发展物理核心素养的好习题.习题的设计思路主要是怎样让你会(相互关联地设问,让你学会做),第(2)问的分层教学将是基于问题解决、发展科学论证素养的实践性案例. 问题1:速度为0的临界点在哪个位置? 考虑竖直面内的圆周运动,物块在粗糙圆轨道外侧的运动问题. 图2 问题1与问题2示意图 如图2所示,设物块到达E点时速度为0,此时OE与竖直方向夹角为α.要求物块能在传送带作用下返回,则α的最大值应满足下列关系式 mgsinα=μmgcosα, tanα=μ. 问题2:h取何值时,物块恰好到E点速度为0? 其中Wf为物块从D到E的过程中克服摩擦力做的功. 问题3:Wf如何计算? 如图3所示,物块在圆轨道外侧运动时,其所受摩擦力是与速度相关的变力.在β从0到α的变化过程,计算克服摩擦力做的功Wf就成为区分不同素养水平的关键所在. 水平1:直接套用熟悉模型,忽略转轮半径0.4 m或误认为转轮可以视为质点,速度为0的临界位置是D点,按参考方法解得临界高度为3 m. 水平2:意识到速度0点的位置偏离D点,但认为转轮半径相对较小,偏离D点很小,就直接取近似求得临界高度为3 m. 图3 问题3示意图 水平3:认识到速度0点的位置偏离D点,但无法确定临界位置或者确定临界位置后发现无法求解,就退而求其次按参考方法求解. 水平4:确定临界位置后,没有意识到摩擦力与速度相关. 设在β位置转过dβ的微小过程中, dWf=f·ds=μmgcosβ·R·dβ, 代入前面各式,解得h=3.14 m. 实际克服摩擦力做功要小于计算值,可知临界高度应小于3.14 m. 水平5:知道摩擦力与速度有关,且严格意义上求解. 当物块位置与圆心连线与竖直方向成β角度时,设其速度为v,则 设在β位置转过dβ的微小过程中 dWf=f·ds=μmgcosβ·R·dβ- 由动能定理可知 则Wf=μmgRsinα- 2μmgR. 结合上述各式,可得h≈3.1 m. 可以看出,试题给出的“3.0 m”控制在可接受范围之内.但不同的方法所花的时间成本差异显著,本题也就无法真正甄别学生真实的素养水平. 指向核心素养的测试题至少具有3个关键特征:(1) 体现课程综合.测试的重点应关注学生通过后天学习形成的综合性学习结果,既可以表现为本学科与跨学科知识技能的整合,还可以体现在隐性知识与价值观念的有机融合.(2) 依托任务情境.创设学生熟悉程度不同的真实任务情境,构建丰富有意义的测试载体,进行科学素养的体验,才可能实现合理的测评,体现学科育人的价值.问题情境越复杂,试题中蕴含的物理规律越隐蔽,对学生的推理和论证能力要求就越高.(3) 指向问题解决.核心素养测评试题的设问总是指向具体任务的问题解决,因为核心素养不仅要求学生掌握课程内容,更注重学生将较复杂的实际问题中的对象和过程转换成物理模型,能在新情境中对综合性物理问题进行分析和推理,获得正确结论并作出解释. 要想编制出科学合理的试题,可根据物理学科核心素养的水平层次、试题情境的复杂性或新颖性、知识要求的深度和广度等方面来设计,保证试题的科学性、规范性和公平性.物理试题的编制及核心素养的测评应保持从教学中来、到教学中去的风格,教师要把所有的教学活动(以及所有的备考活动)都围绕试题所反映的素养目标,而不是测试本身.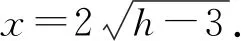
2 从参考答案看设计思路
3 科学论证取向的问题解决教学
4 科学论证取向的试题编制
——“模型类”相关试题选登

