电主轴电机的温度场建模研究

刘建平　毕根凤

摘   要：内置电机的发热是电主轴的主要内部热源之一，内部温度较难获取，温度场复杂，本文基于电主轴内置电机的结构特点和传热学理论，考虑到冷却系统对内置电机的散热影响，分析并简化了内置电机的热边界条件，提出了稳态温度场分析方法，基于热阻网络法构建了电主轴电机的稳态温度场数学模型，并通过仿真分析验证了模型的准确性。内置电机温度场数学模型的建立简化了复杂的温度场求解问题，对于获得电主轴系统温度场分布及主轴使用性能等工程问题有着重要的理论指导意义。

关键词：电主轴  内置电机  热阻网络  温度场  仿真分析

中图分类号：TG659                                 文獻标识码：A                         文章编号：1674-098X（2019）07（a）-0117-02

1  绪论

高速机床的主轴是由内装式电动机直接驱动的，从而把机床主传动链的长度缩短为零，实现了机床主轴的“零传动”[1]。电机和轴承是电主轴系统的两大主要内热源，内置电动机的发热对电主轴的温升有很大影响，如果不加以控制，由此引起的热变形会严重降低机床的加工精度和轴承使用寿命，从而导致电主轴的使用寿命缩短。电主轴由于采用内藏式主轴结构形式，位于主轴单元体中的电机不能采用风扇散热，因此自然散热条件较差。电机在实现能量转换过程中，内部产生功率损耗，从而使电机发热。对电机产生发热的主要解决方法是对电机定子采用冷却液的循环流动来实行强制冷却。

2  电主轴内置电机稳态温度场数学建模

为了简化电主轴内置电机的稳态分析计算，作如下简化：

（1）内置电机部分属于一维导热，忽略端部效应;

（2）内置电机视为内热源，且发热均匀;

（3）主轴各个部件为常物性，且接触良好;

（4）内热源产生的全部热由冷却介质带走。

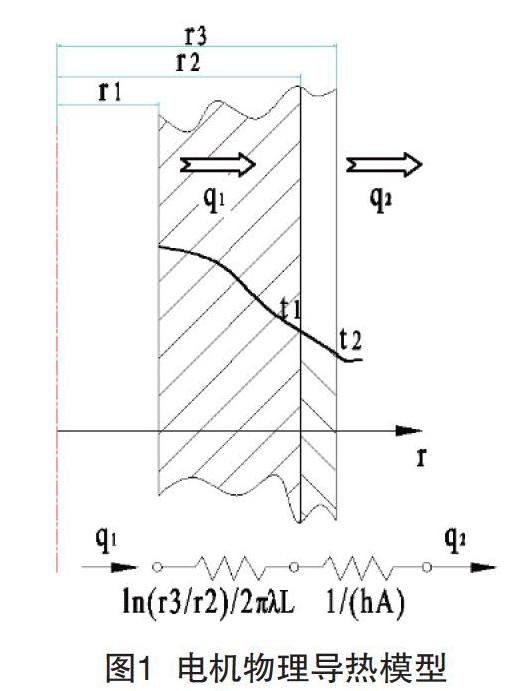
将内置电机视为整体，分析计算电机—水道壁—流体介质的导热过程及温度场分布，图1形象地表述了电机—水道壁—流体介质之间的热流及热阻情况，基于热阻网络模型展示了电主轴内置电机的物理导热过程。

3  电主轴内置电机温度场仿真分析

若系统的净流为零，即流入的热量加上系统自身产生的热量等于流出系统的热量[6]：，则系统热稳态。稳态热分析的能量平衡方程以矩阵形式，见式（4）：

式中：[K]为热传导矩阵，包含热系数、对流系数及辐射和形状系数;{T}为节点温度向量;{Q}为节点热流率向量。

ANSYS利用模型几何参数、材料热性能参数以及所施加的边界条件，生成[K]{T}及{Q}。

稳态分析基于热传导方程，不考虑任何时间相关的瞬态效应。载荷和约束包括热生成、热通量、热流率、对流及辐射。基于电主轴整体结构特征，本文将其视为轴对称结构。电机的定子和转子、轴承部分均可当作厚壁圆筒，定子冷却套上的冷却水道壁可当作薄壁圆筒，螺旋槽可等效为圆环形。

电主轴内置电机在实现能量转换过程中，内部功率损耗，从而使电机产生大量的热。本文中对电机产生发热的主要解决方法是对电机外圈采用冷却液的循环流动来实行强制冷却。建立正确的有限元模型是进行热态分析的基础，基于电主轴内置电机及冷却水道的结构特点，简化几何结构为长圆环，对其进行网格划分。

添加材料属性，对于热稳态分析，物体的导热系数是关键参数，设置边界条件进行ansys仿真分析，验证电主轴内置电机理论模型的正确性。通过仿真分析得到如图1所示的电机温度场分布，输入冷却水道水温值为15℃，当电主轴处于热稳态时，此时电机转子最高温度为32.524℃，内置电机定子与冷却道接触部位的温度约为24.587℃，电机冷却道壁与冷却介质接触部位的温度为：23.595℃与理论模型分析结果对比，误差为3%左右，可见仿真分析进一步验证了模型的理论正确性。

4  结语

（1）内置电机的发热是电主轴的主要内部热源之一，基于电主轴内置电机温度场数学模型，得到电机稳态温度时转子温升最大。

（2）冷却系统是内置电机的主要散热系统，电主轴冷却系统给定不同温度的介质，将得到稳态下电机径向各处温度值。

（3）通过仿真分析验证了文中简化模型的正确性，仿真结果与理论模型分析结果误差为3%左右，为对于获得电主轴内置电机系统温度场分布及电主轴热态使用性能等工程问题有着重要的理论指导意义。

参考文献

[1] 张柏霖，张志润，肖曙红.超高速加工与机床的零传动[J].中国机械工程，1996，7（5）：37-41.

[2] 黄晓明.高速电主轴热态特性的有限元分析[D].广东工业大学，2003.

[3] 王泽鹏，张秀辉，胡仁喜，等.ANSYS 12.0热力学有限元分析从入门到精通[M].北京：机械工业出版社，2010.