深度约束下的声速估算∗

孟庆波 王振杰

(中国石油大学(华东)地球科学与技术学院 青岛 266580)

0 引言

高精度的水下定位技术在海洋勘探、矿产资源开发、水下运动目标的导航定位等领域具有重要的应用价值[1−2]。由于卫星定位中使用的电磁波会被海水衰减吸收，而声波在水中具有良好的传播性，当前的水下定位基本应用水声进行通信[3]。进行水下目标定位时，浮标等与水下目标的距离R是通过测量浮标到目标物的时延信号和声速计算得出。现在高精度时延检测技术在一定范围内检测精度可达微秒级别，然而声速会随温度、深度、盐度的变化而变化，在垂直方向上并不是均匀分布[4]，如图1所示。因此声线弯曲误差是对距离R的精确计算的主要影响因素。

图1 声速剖面Fig.1 Sound velocity profile

在获取到精确声速剖面情况下，国内外专家学者对声速改正的研究大致有以下几种方法：等效声速剖面法、加权平均声速法、经验声速法、多项式展开法、声线跟踪法、有效声速查表建表法、神经网络法等。Geng 等[4]在1999年提出等效声速剖面法观点，其思想是计算波束脚印时，在相同的传播时间内，如果两条不同声速其声速和深度所围成的面积相等，则认为两条声速剖面是等效的，即对于实际中复杂的声速剖面曲线，总可以找到一条恒等梯度声速或者等声速来替代；加权平均声速法是将不同深度的声速用平均声速的定义计算平均声速，将计算得到的声速作为初始声速，此方法简单、应用较广，但精度较低[5−6]；经验声速法是将经验声速写为平均声速、水深及俯仰角的函数[7]；多项式展开法中泰勒级数展开法是常用的方法，此方法是在平均声速处展开成泰勒级数，展开系数是俯仰角函数[8]；声线跟踪法是一种精确方法，将水层按照一定深度间隔分为多层，根据Snell 定律逐层跟踪迭代计算，又分为分层等声速跟踪和分层等梯度跟踪法[9−10]；Vinecent 等[11]提出有效声速概念，并通过建表查表建立声源与目标间的有效声速信息，孙万卿[12]也基于此对浅海声速进行了研究；神经网络法[13]在神经网络的训练及样本选择上仍然存在问题。在无声速剖面的情况下，Yang 等[14]利用测距误差和传播时间的二次关系实现了无声剖的水下目标静态定位，此外鲜有对无声速剖面的研究。

本文在无声速剖面数据情况下，提出了一种基于深度约束，根据浮标与水下目标的空间几何距离进行声速估算的方法。通过仿真实验与浅海实验数据证明了该方法有效可行，且满足一定的定位需求。

1 定位原理

假设某时刻水下目标位置为(X,Y,Z)，海上布设的浮标位置分别为(X1,Y1,Z1)、(X2,Y2,Z2)、(X3,Y3,Z3)，水下目标到浮标的时延分别是t1、t2、t3，采用的声速为C，则浮标至目标的距离Ri=Cti(i=1,2,3,···)。根据“圆定位”公式得[15]

通过解方程便可得到目标的位置(X,Y,Z)，当有多组历元的观测时可根据最小二乘的原理求取出目标的最佳坐标估值[16]。

2 深度约束下有效声速估算

当前水下目标装备有压力传感器，一般带有温度补偿的石英压力传感器精度可达0.01%F.S，可测出目标至海面的距离[17−18]。当水面平静无波动时，深度为一常数。由于海浪作用或者风力潮汐影响，实际海面是波动的，深度D为

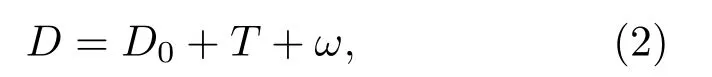
式(2)中，D为观测水深，即压力计测量数；D0为平均海水面至水下目标距离；T为潮汐的振幅；ω为波浪影响。赵建虎等[18]指出，波浪的周期为几秒到几分钟不等，水位周期较长，10 min 内可视为无变化。而短时间内可以借助平滑公式消除ω影响：

式(3)中，D0i为第i个深度数据的平滑滤波结果；m为滤波窗口大小。

以平滑滤波后的D为深度约束，通过比较计算得出深度Z与D的差异，根据浮标与水下目标的空间几何距离对声速进行修正。具体步骤如下：

如图2所示，将初始声速C0带入公式(1)得出目标的一个位置B(XB,YB,ZB)，将B垂直投影到深度平面上，交点为B′。由“圆定位”原理得知，在时间测量准确的情况下，定位误差是由声速偏差引起的交会半径误差造成的。选取海面任意一个浮标(如浮标A)，可得浮标与估计位置B的距离R=AB=C × t，与投影点B′的距离R′=AB′=(C+∆C)×t，由此得

其中，D为根据目标传感器所得改正后的深度，(XA,YA,ZA)为选择的浮标A坐标，(XB,YB,ZB)是由公式(1)计算得出的水下目标坐标

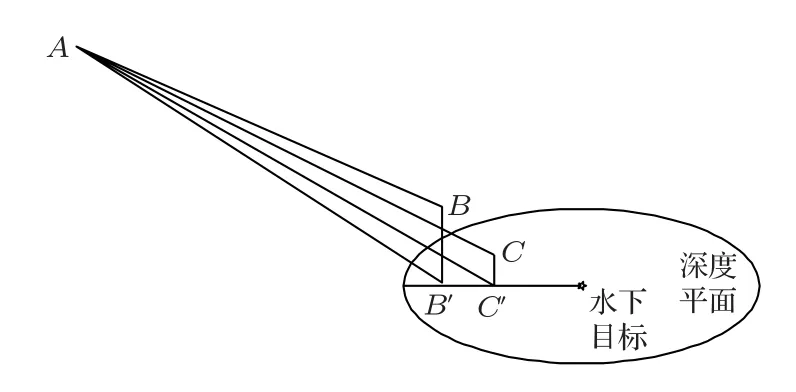
图2 声速修正示意图Fig.2 Sound speed correction

根据定位精度给出一个判定值ε，第i次声速改正后所计算的深度为zi，当zi满足|zi −D| < ε时，认为目标位置符合定位精度要求。否则按照下列条件对声速进行以下修正：

将改正的新的声速Ci+1带入公式(1)得到新的目标坐标(x′,y′,z′)，如图2中点C的位置，再次判断z′与D的关系是否满足精度，若不满足重复公式(4)∼(8)进行迭代修正，直至满足精度；若满足精度，将求得的声速值带入公式(1)求得水下目标坐标(x,y,z)。以上步骤的流程示意图如图3所示。

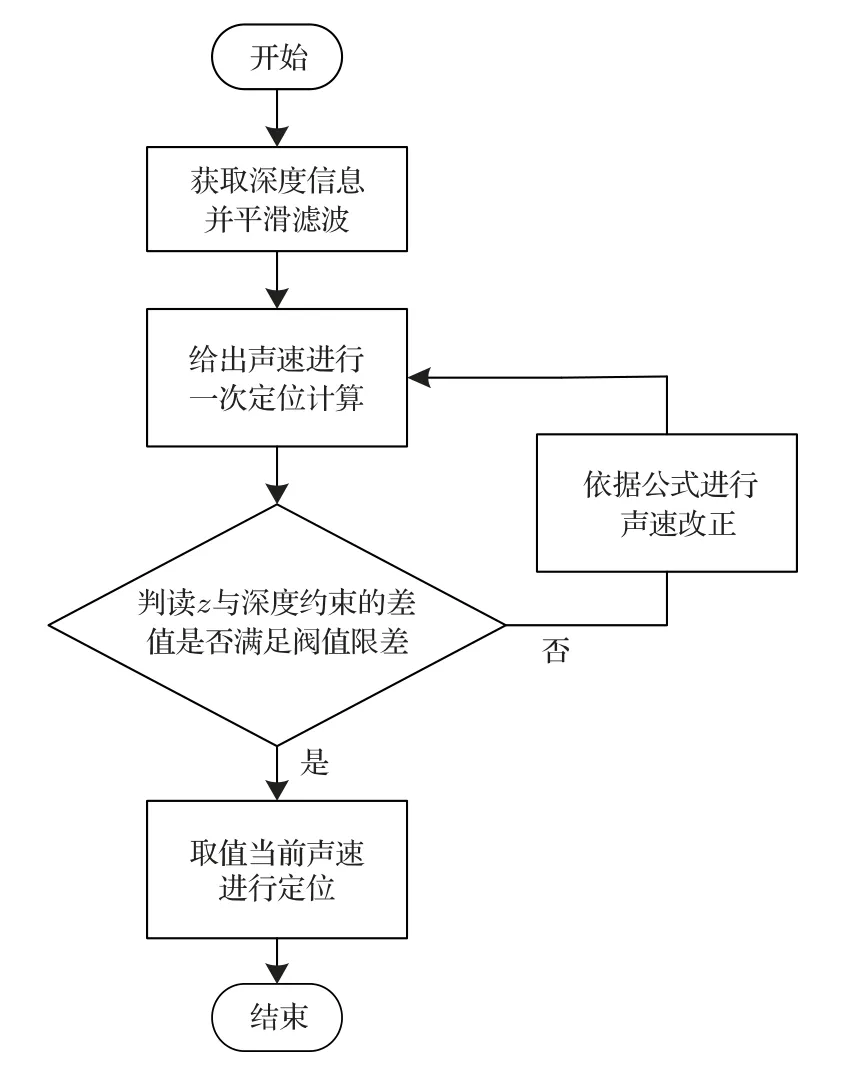
图3 技术流程图Fig.3 Technical flow chart

3 仿真算例及结果分析

模拟四个浮标布设成正方形，浮标中心间距模拟为4000 m。海面波浪运动模拟为2 m 的余弦波动。海底模拟的应答器A 的坐标为(500 m,500 m,−2000 m)，此外还布设了B(0,500 m,−2000 m)、C(0,0,−2000 m)、D(500 m,0,−2000 m)三个应答器，浮标及应答器位置如图4所示。模拟水域实测声速剖面为编号241911 的HM2000 型Argo 浮标获取的南海声速剖面，声速结构如图1所示，用与验证本文方法和计算其他方法声速值。实验模拟误差，设置偶然误差方面换能器定位中误差各方向为10 cm，应答器时延误差5 cm，系统误差模拟参考文献[19–20]中的方法。

由于波浪潮汐的作用，获取到的深度是波动的，根据平滑滤波公式(3)滤波之后，可得一个稳定的深度信息，如图5所示，滤波后深度为2000.084 m。

图4 浮标及水下目标模拟位置示意图Fig.4 Buoy and underwater target simulation position

图5 压力传感器深度及滤波后深度Fig.5 Pressure sensor depth and post-filter depth

图6 各迭代次数声速值Fig.6 Sound speed of each iteration

初始计算时声速为表层声速1538.903 m/s，ε值的设定为0.001，即计算的深度与实际深度约束给出的差值在±1 mm 范围内时的声速为最终估计声速。选取浮标1 和水下目标A 进行估算，表1和图6表示了每次迭代中的声速改正值及声速的变化曲线。从表1可以得出，经过10次迭代声速趋于稳定，前四次迭代中，声速的改正数比较大，说明此时与实际有效声速相差比较大，随着迭代次数的增加，声速越来越接近实际有效声速，改正数值逐渐减少，最终迭代终止声速为1493.534 m/s，在图6中也可以看出，当迭代次数到达5 次以后时，声速曲线波动较小，近乎平直，改正值在0.1 m/s内。

表2记录的是每次迭代次数中水下应答器坐标与其真值的差值，可以看出随着迭代次数的增加，计算的深度与实际深度平面之间的差值越来越小，逐步收敛满足限差要求。结合表1可以看出，在每次的迭代计算中若计算的深度值大于实际深度值时，声速的改正为负数；若计算深度值小于实际的深度值时，改正为正数，验证了本文方法思路是正确有效的。

为了验证最终估计声速是否满足定位需求，将本文方法所得声速与加权平均声速法、泰勒级数展开法、等效声速法对四个水下应答器的定位结果进行了比较，分别统计每个浮标X、Y、Z方向上相对于坐标真值的差异∆X、∆Y、∆Z，结果如图7所示。同时计算了四种方法的定位均方根(Root mean square，RMS)值。本文方法定位结果的RMS为0.671 m，加权平均声速法、泰勒级数展开法、等效声速法三种方法的RMS 分别为1.523 m、0.723 m、0.885 m。从均方根大小以及图7可以得出本文提出的方法所估计的声速满足定位需求，定位结果优于其他三种方法。其中水平XY方向的定位精度与泰勒级数展开方法、等效声速法接近，远高于加权平均声速法的定位结果，在垂直Z方向上，由于本文方法使用了深度约束，垂直方向定位精度远高于其他三种方法。

表1 各迭代次数后声速值Table1 Sound speed after each iteration

表2 迭代次数中各方向坐标与实际坐标差值Table2 Difference between the estimated position and the actual

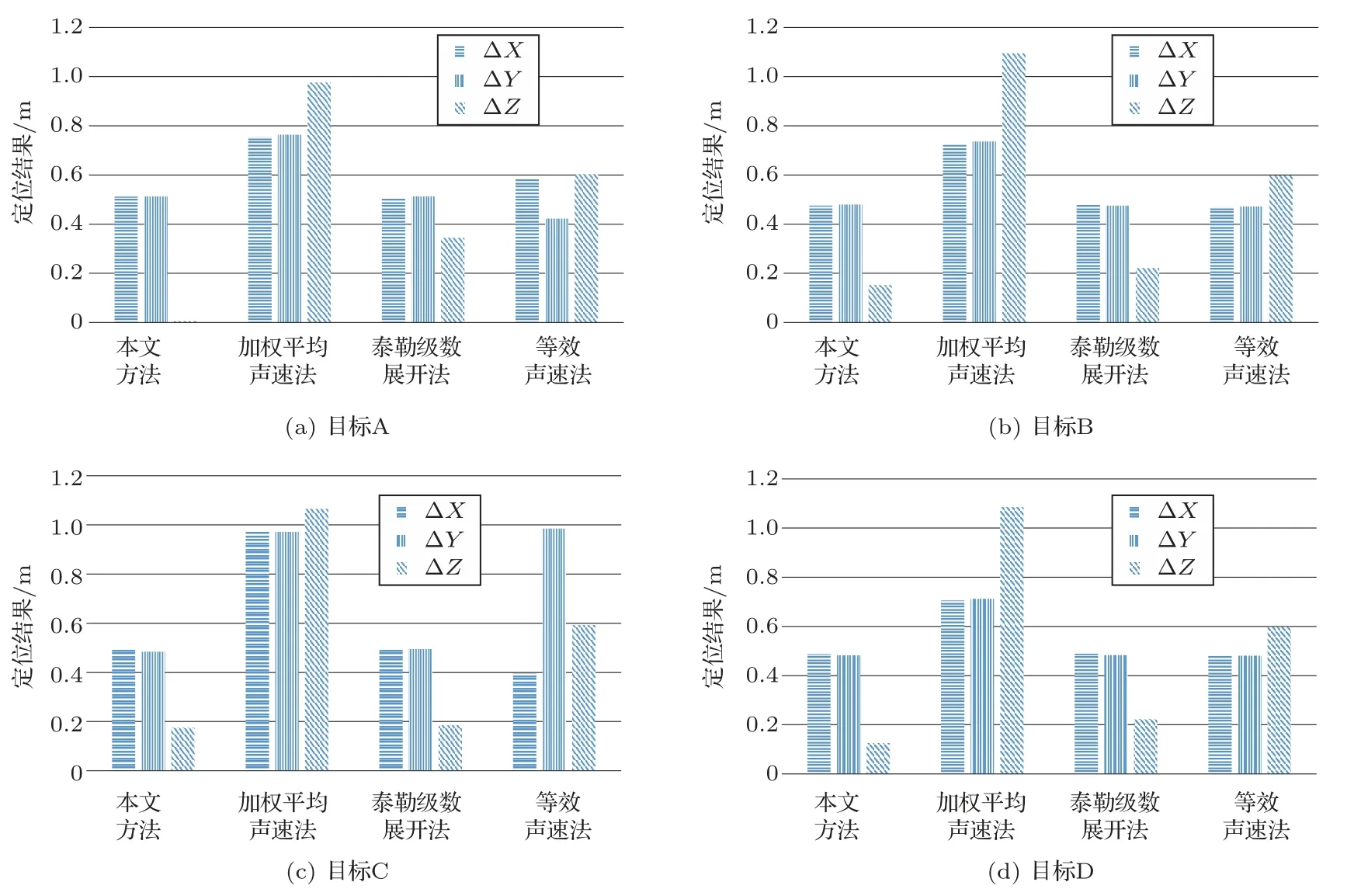
图7 仿真定位结果比较Fig.7 Comparison of simulation positioning results

图8 约束深度与定位误差关系Fig.8 Relationship between constraint depth and positioning error

在实际测量中，由于仪器精度或外界环境的影响，获取的作为约束的深度并不总是精确的。为了确定定位误差与约束深度误差之间的关系，设定模拟的测深误差在±10 m 之内，得到定位RMS 值随深度误差变化的曲线，如图8所示。从图8中可以看出，定位误差随深度误差的增大而增大，两者近似为正比例的线性关系。结合图6及表2数据可以推断，这是由于深度误差造成了估计声速的误差，而估计声速误差对Z方向坐标影响远大于XY方向。

4 实测验证与结果分析

实测数据采用青岛灵山岛附近海域实验数据(N35◦46′42′′,E120◦12′57.91′′)。数据采集记录时间为2017年12月1日8点–10点。船上搭载有电罗经、GPS、测深系统、声速剖面仪(CTD)及声学定位系统，测区水深约24 m，水下布置单信标。采用“走航式”观测手段，以信标为中心进行“画圆”与“画十字”观测，采样间隔为2 s。声速剖面采样间隔为0.3 m，采集的声速用于验证文章方法和计算对照方法的声速值。图9和图10 分别表示实验区测量船GPS 航行轨迹、应答器位置及区域声速剖面。

对原始观测文件进行数据处理后，分别计算加权平均声速法、泰勒级数展开法、等效声速剖面法和本文方法所得到的声速，其中等效声速剖面法使用表层声速C0及等效梯度g来表示。将坐标解算值与实测结果(作为坐标真值)进行偏差比较，表3给出了单点解算坐标偏差统计结果。

从表3可以看出，在平面XY两方向的精度方面，四种方法的精度接近；由于本文方法使用测试区水深作为约束条件，Z方向的精度明显高于其他三种方法。四种方法的RMS 差值不大，最大约为0.07 m，分析这是由于测试区的最大水深为24 m左右，浅水区的声线对应声程较短，与声速有关的误差远没有深海区显著，理论上本文方法在深水区的声学定位中优势会更为突出，但具体性能表现还须后续深海数据验证。

图9 测量船轨迹及应答器位置Fig.9 Ship trace and transponder’s position

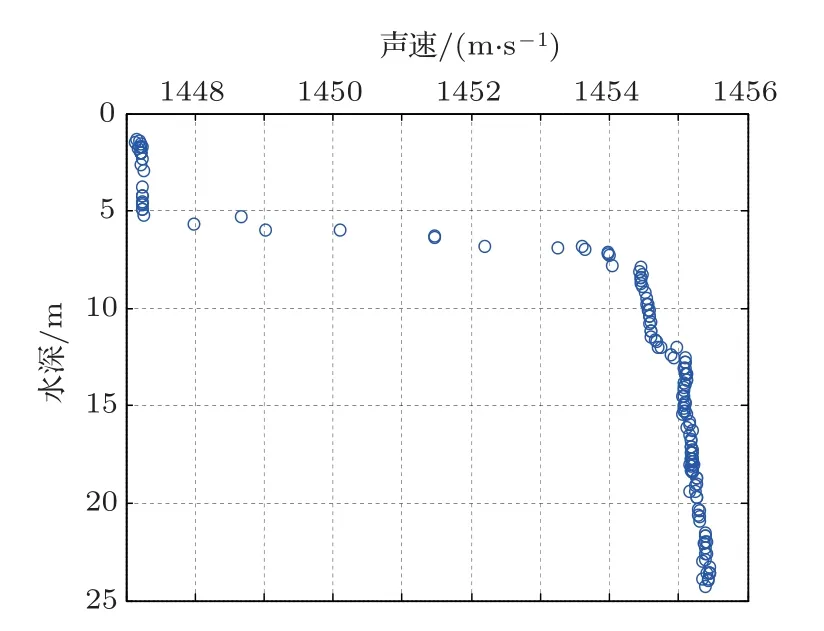
图10 测试区声速剖面Fig.10 Sound velocity profile of the test area

表3 解算结果偏差统计Table3 Calculation results statistics table

5 结论

本文提出了一种基于深度约束的无声速剖面的有效声速估计方法，其最后求取到是声源至应答器之间的一种平均声速。通过实验验证了该方法可行，所得估计声速满足定位要求，理论上该方法可不需要获取声速剖面信息，减少声速剖面仪的使用；也可根据历元观测进行声速实时调整，在实际生产中节约成本，减少重复劳作。

此外本文仍有以下几点探讨与说明：

(1)文章方法基于测量的深度进行声速估计，对于深度获取的精度依赖较高，最终获取的声速及定位误差会随着测量深度误差的增大而增大。

(2)由于本文方法的有效性建立在实验室仿真实验与浅海实验数据验证上，还有待进一步深海实测数据验证。