用“变”与“不变”思想进行数学复习

王少平

摘   要：数学是运动变化的，且在运动变化中显示“变”与“不变”的独特魅力，彰显其内在的规律性，体现知识间的前后联系。“变”与“不变”作为一个重要的数学思想应在学生的数学学习中予以渗透，以便学生领悟并能运用知识间的联系建构系统的知识网络。在复习课中渗透“变”与“不变”思想，有利于学生发现知识间的联系，对知识进行整理和重组，将“变”与“不变”思想转化为解决问题的一种模式，利于知识的保持、迁移和运用，从而促进数学思维提升，提高问题解决能力。

关键词：小学数学;数学复习;“变”与“不变”;教学策略

中图分类号：G623.5    文献标识码：A    文章编号：1009-010X（2019）28-0021-03

“万物皆变”，这是哲学基本理念。既有“变”，就有“不变”。在数学中以“变”与“不变”为主线，锁定主要教学内容，既有利于创设良好的认知环境，又能让学生多一些哲学高度的思考。拿数学复习课来说，复习课的主旨就在于让学生透过变化的情境和信息去抓住其中不变的本质。复习课上利用“变”与“不变”的关系引导学生透过现象看本质，让其立足哲学的视野进行理性地思考：体悟、描述“变”与“不变，探寻、应用“变”与“不变”。促使他们养成对事物、对生活的态度：千变万化的事物存在怎样的联系？这些联系可以帮助我们有哪些新发现？这样的复习课让学生从繁杂的机械训练中走出来，借助数学问题、数学关系、数学特点吸引学生，建构清晰的知识网络，让数学复习课焕发出应有的数学魅力。

再者，复习课中教师本应帮助学生建立起一个具有联系性的知识体系，使之成为个人内部知识网络的一部分，这样才更利于学生知识的长久保持、迁移和运用。然而，很多教师在上复习课时总是占用大量时间让学生回忆“学习了哪些知识”，让其在带有明确指向性的问题牵引下，将已学的知识点一一说出。在这种复习中，知识点之间的联系主要表现为线性的、单向的，无法建立完善的认知结构，无法让学生的思维向纵深处发展，且像这种碎片化的知识点罗列，会阻碍知识的深度理解和迁移运用。

本文以小学数学六年级“立体图形的复习”为例，谈一谈教师如何从“变”与“不变”的角度引导学生展开空间推理，寻找新旧知识间的内在关联;如何在“变”中寻求“不变”，促进知识的整理和重组，建构立体的知识网络;如何抓住“不变”探寻解决问题的思路，构建问题解决的策略，提升数学思维品质。

一、在运动变化中引发联想，体悟“变”與“不变”

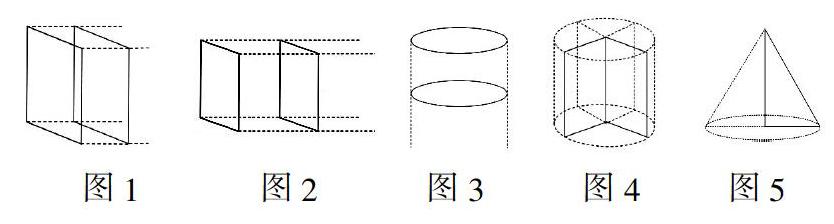
【案例描述】教师用PPT出示长方体、正方体、圆柱体、圆锥体这几个立体图形，提问：这几个立体图形分别可以用什么样的平面图形通过何种运动方式转化而来？立体图形与平面图形之间有什么联系？学生思考回答并结合PPT的动态演示，借助透视图（见下图）进行空间想象，

并语言描述：平面图形经平移或旋转运动后，其运动轨迹形成了一个立体图形，平面图形成了立体图形的一部分。并且原来的平面图形与转化后的立体图形之间存在着诸多联系。图1：长方形成了长方体中的一个侧面，长方形的长成了长方体的高，长方形的宽成了长方体的宽，长方形的面积成了长方体侧面（左或右）的面积，长方形向右平移的距离就是长方体的长;图2：原来的正方形成了正方体中的一个面，正方形向右平移的距离等于正方体的棱长，正方形的边长与正方体棱长相等;图3：圆向下平移的距离就是圆柱体的高，圆成了圆柱体的底面，圆的半径就是圆柱体的底面半径;图4：原来长方形的长成了圆柱体的高，长方形的宽成为了圆柱体的底面半径，长方形的面积是圆柱体纵切面面积的一半;图5：直角三角形中作为轴的一条直角边成了圆锥体的高，另一条直角边成为了圆锥体的底面半径，三角形的面积是圆锥体纵切面面积的一半……

【案例评析】 学生通过空间想象与直观透视图的观察，明晰了二维的平面图形转化为三维的立体图形后，图形的形状虽然变了，但转化后的立体图形并不是孤立的个体存在，而是与原来的平面图形有着千丝万缕的联系。这个“联系”就是学生在“变”的表象背后所看到的“不变”。这些“不变”的联系从一维的边线到二维的平面、再到三维的立体，均在学生的脑中、眼中、口中一一呈现。这一过程既让学生初步感知了二维的平面图形转化为三维的立体图形后的“变”与“不变”，激发起学生的空间想象，又沟通了新旧知识间的联系，利于架构一个立体的知识网络，同时也潜移默化地融入了“数学”是发展变化的这一本质内涵。

二、在操作变化中寻求联系，描述“变”与“不变”

上一环节是让学生在运动变化中直观感知由平面到立体的联系，这一环节则是结合一定情境将“操作”与“面、体的计算”相融合，让学生在自主选择操作方式中实现变式练习，明晰“变”与“不变”相互依存，渗透辩证思想。

【案例描述】师：在学习立体图形时，我们经常会通过“切”“削”“拼”“熔”的操作，将立体图形“变形”，从而产生很多新问题。比如：将两个完全一样的正方体拼成一个长方体、将一个圆柱体削成一个最大的圆锥体、将一块正方体形状的方钢锻造熔铸成一块圆柱体形状的钢柱……变形之后的立体图形与原来的立体图形之间有什么联系？请选择“切”“削”“拼”“熔”中的一种方法将一个立体图形变形，然后再说一说变形前后“什么变了，什么没变？”

学生1：用“削”的办法，把圆柱削成和它等底等高的圆锥，形状变了，体积只是原来的三分之一，但底与高不变。

学生2：选用“切”的办法，在长方体中切出一个最大的正方体，体积变了，但切出的正方体的棱长是原长方体中最短的一条棱的长度。

学生3：采用“拼”的方法，把两个一样的正方体拼成一个长方体，形状变了，长方体的体积是原来正方体的2倍，正方体的面成了长方体中的侧面。

学生4：用“熔”的方法，把一个正方体方钢锻造成一个长方体，形状变了，体积没变。

【案例评析】这一环节中的“切、削、拼、熔……”不仅仅是外在的操作方式，还转化为用来传意的工具，学生据此进行表达和交流，灵活运用已有知识进行题型变换，让学生对立体图形中“表面积与体积的计算”知识进行了整体回顾与把握。

三、在情境中聚焦“不变”，探寻问题解决的突破口

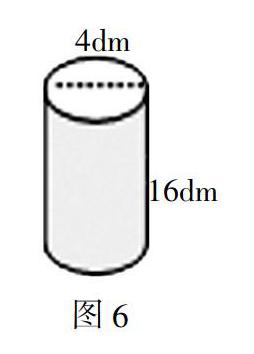
【案例描述】 教师出示圆柱（图6），底面直径4分米，高16分米。出示下列问题：

问题1：把这个圆柱削成一个

最大的圆锥，应该削去多少？

问题2：把这段圆柱沿底面直

径纵切一刀，表面积增加多少？

问题3：给这个圆柱形拼接上

10分米长的一段，表面积增加多少？

问题4：把它锻造成一个等底的圆锥，圆锥的高是多少？

师提问，找出每道题中图形变化前后的联系，即“不变”的地方，并说说解题的思路。

学生思考后回答，摘录如下：

问题1：削成的圆锥与圆柱等底等高，所以圆柱体积的■就是削去的量。

问题2：纵切面的长和宽就是圆柱的高和底，16×4×2就是增加的表面积。

问题3：拼接上的底面与圆柱的底面相等，用底面周长乘拼接的长就是增加的表面积。

问题4：圆柱和圆锥的体积与底面积相等，利用圆锥的体积计算公式即可算出圆锥的高。

【案例评析】教师通过设计有联系的题组，先让学生寻找问题中“不变”的地方，依托“不变”，挖掘出圆柱变化前后的“联系”，找到解决问题的思路。寻求“变化”背后的“不变”，才是解决问题的突破口。“变”与“不变”作为一种数学思想已内化为认知思维中问题解决的策略，唤醒了学生解决问题的策略意识。在寻找“变与不变”中，各个知识点也在学生头脑中连成线、织成网，促成知识结构重组，从而达到复习的目的。

四、应用中内化“变”与“不变”思想，构建解决问题的模型

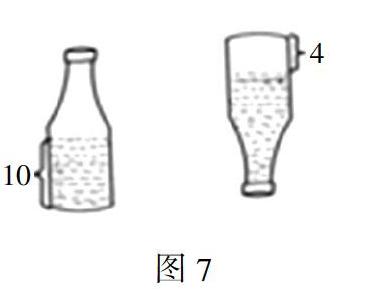
【案例描述】 PPT出示：“将一个玻璃瓶子正立（图7），底面直径是8厘米，水的高度是10厘米;再将玻璃瓶倒立，空着部分的高度是4厘米。这个玻璃瓶的容积是多少？”

学生思考交流：不管瓶子是“正立”还是“倒立”，瓶子中水的形状变了，但是水的体积不变。讨论汇报：第一个瓶子中水的体积加上第二个瓶子中空的部分的体积，就是整个瓶子的容积。补充：因为水的体积不变，第一个瓶子中空白部分是不规则的，所以用第一个瓶子中水的体积加上第二个瓶子空的部分的体积。

【案例评析】学生无需教师的指导和点拨，自觉运用“变”与“不变”思想找到了解决问题的思路。在语言表述中学生思路清晰、縝密。显然，在“变”中寻求“不变”，已作为一种问题解决的策略被学生吸纳和运用。在语言表述中学生思维的主动性和严谨性无疑是策略意识外化的表现。

纵观本节课，将“联系”的观点贯穿始终，跳出了传统复习课“单纯回忆”的怪圈，也不再是大量的机械训练，而是让学生一直在“变”与“不变”中进行理性思辨，打通了一维的边线、二维的平面和三维的立体图形间的联系。学生形成了运用“变与不变”思想解决问题的策略，提升了数学思维品质和解决问题能力。同时，他们学会了运用运动变化的观点去审视周围的事物，透过“变化”的表象去深究事物内在的本质联系，于潜移默化中提升数学素养，这应该是本节课教学的真正价值所在。