考虑湖盆摩阻效应的川藏铁路冰碛堰塞湖地震涌浪及溃决风险分析

田林桃,姚令侃,2,3,邓 桃,张 聪,黄艺丹,2,3

(1.西南交通大学土木工程学院,成都 610031； 2.高速铁路线路工程教育部重点实验室,成都 610031；3.陆地交通地质灾害防治技术国家工程实验室,成都 610031)

我国对地震涌浪的研究相对较少，目前相关研究成果主要来自于国外学者。佐藤清一(1967)在忽略水体的黏性、压缩性、动水压以及边壁反射，并限制在只有流体上流面能传递水波运动的假定上建立了半无穷边界的计算模型；同时以长波理论简化N-S方程并建立控制方程，且在将地震运动简化为坝体正弦运动的基础上得到了波高的解析解[1]。Vincenzo Armenia(1996)等利用雷诺平均Navier-stokes方程和浅水波方程建立了数值模型，并开展了水箱做周期运动的数值模拟，最终利用模拟数据对数值模型进行检验；该水箱模型考虑了流体黏性和外界非线性扰动，相较于佐藤清一的计算模型更具进步性[2]。Ismail Aydin (2012) 基于半无限边界高水位的水体模型，利用数值模拟方法研究坝面涌浪，得到了地震涌浪高度取决于地震动峰值速度、振动周期、水深的结论，并建立了坝面涌浪计算公式；根据该公式可预测涌浪漫顶的临界地震动峰值速度等参数[3]。土耳其的Ender Demirel(2016)使用了8组实测地震数据进行坝面涌浪的数值模拟，得出地震时坝面最大涌浪高度主要受地震动峰值速度PGV和水深控制，从而建立以二者为自变量的经验公式，并利用实测地震数据对涌浪模拟结果进行验证[4]，该篇论文首次利用了实震数据，较Ismail Aydin的纯数值模型更具普适性和说服力，是反映地震涌浪研究的最新成果。但以上公式均是以高坝大库为研究对象提出的，均忽略了湖盆底部的摩阻效应。

川藏铁路的建设受到全世界的关注。目前成都至雅安段已于2018年底开通运营，林芝至拉萨段正在紧锣密鼓地修建中，并已基本完成了雅安至林芝段的可研工作和勘察设计工作。川藏铁路雅安至林芝段将会经过藏东南区域，此区域分布发育了我国罕有的海洋性山谷冰川类型，海洋性冰川活动性强，形成了大量的冰斗、终碛或侧碛垄、冰川堵塞水流通道等地貌现象，因此形成大量冰湖[5]。例如川藏公路的然乌至培龙段(长222 km)沿公路两侧支沟内，有规模不同的冰川461条在其中发育，大小冰湖131个分布其间，而在这些冰湖中有80个冰碛堰塞湖较易发生溃决。近40年来，造成公路断道20 d以上至270 d的大规模冰湖、冰崩湖溃决洪水泥石流[6-7]8次，冰湖溃决后又形成泥石流坝溃决5次，可见堰塞湖溃决洪水已成为对线路方案起控制作用的灾害类型[8]。由于川藏铁路沿线冰碛堰塞湖大部分位于高烈度地震区，地震涌浪无疑是导致冰湖溃决的主要诱因之一[9]。

冰碛堰塞湖即冰碛物堰塞冰川槽谷形成的湖泊，其一大特点是，相对于滑坡形成的堰塞湖而言规模较小且冰碛物组成的湖底糙率较大[10]，如根据目前对帕隆藏布流域冰碛堰塞湖的初步统计结果，库容从0.7万m3至3 328万m3，深度为2～35 m。认为地震时湖盆发生振动，底层水体将因为湖盆底部的摩阻效应的作用发生同步运动，水体获得的能量将逐步从下层向上层传递并在表面产生涌浪。地震涌浪计算时应考虑湖盆底部的摩阻效应，对于水深较浅的冰碛堰塞湖更不能忽略，现有的涌浪计算公式并不适用，必须建立符合实际的涌浪计算公式，以指导川藏铁路勘察设计工作。鉴于此，首先设计了底部加糙的大型振动台模型实验，通过对实验数据的拟合，建立了考虑摩阻效应的地震涌浪计算公式，并结合临界溃决水深公式，提出了冰碛堰塞湖溃决风险评估方法，希望能为川藏铁路制定灾害风险调控对策提供科学依据。

1 振动台造波模型实验及结果分析

1.1 振动台

本实验依托西南交通大学高速铁路线路工程教育部重点实验室的电液伺服驱动式地震模拟振动台开展，其主要技术指标如下。

模型水箱尺寸为：3.75 m×1.75 m×1.51 m；

系统频率范围：0.4～15 Hz；

系统最大加速度为：1.2g(频率范围：5～15 Hz)；

水平方向振动有效负荷质量：25 t；

工作平台的台面尺寸：4 m×2 m；

控制方式：开环(离线修正)，共有位移、加速度控制两种方式；

激振方向：水平。

实验振动台见图1。

图1 振动台

1.2 振动台造波模型实验

1.2.1 振动台模型参数设置

表1 冰湖原型及实验模型数据

1.2.2 实验设计及验证

为研究考虑湖盆摩阻效应的地震涌浪，开展振动台造波模型实验，实验装置如图2所示。水箱从中部到边壁的区域布置了6个浪高仪来测量实验中地震涌浪浪高变化过程，编号为A1～A6，布置方式如图3所示。

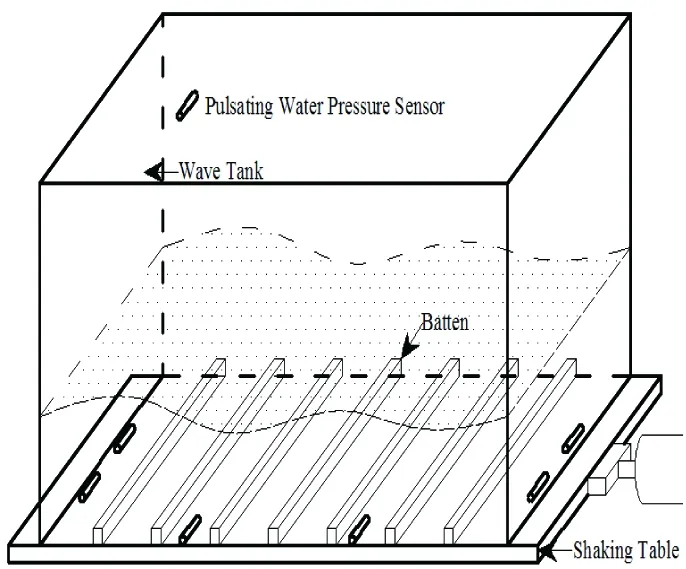
图2 实验装置

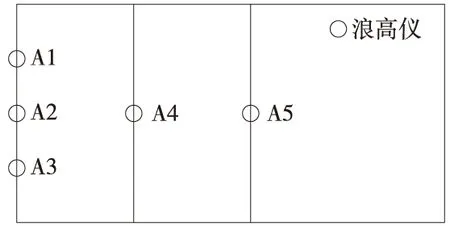
图3 浪高仪布置

实验中潜坝的布设方式依据文献[17-18]对糙率与群潜坝的研究，使用2 cm×2 cm×1.75 m的木条作为潜坝，以坝间距为37.5 cm的形式均布于水箱底部，布置方式见图4。

图4 实验区域

共设置4组初始水深，每组水深包括4个不同的地震峰值加速度，这样按表2所示实验参数共计开展16组实验。

表2 实验参数

以2008年“5.12”汶川8.0级地震时卧龙站记录的南北向的地震波作为振动台输入信号，振动台对模型水箱的晃动过程就模拟了地震对水体的作用过程。在完成上述实验设计后，另设计了模型箱底部光滑的实验，将实验数据与忽略摩阻效应条件下理论较严密的Demirel公式的计算值进行对比，以验证振动台造波模型的合理性，实验结果见表3。然后开展底部加糙的地震涌浪实验。

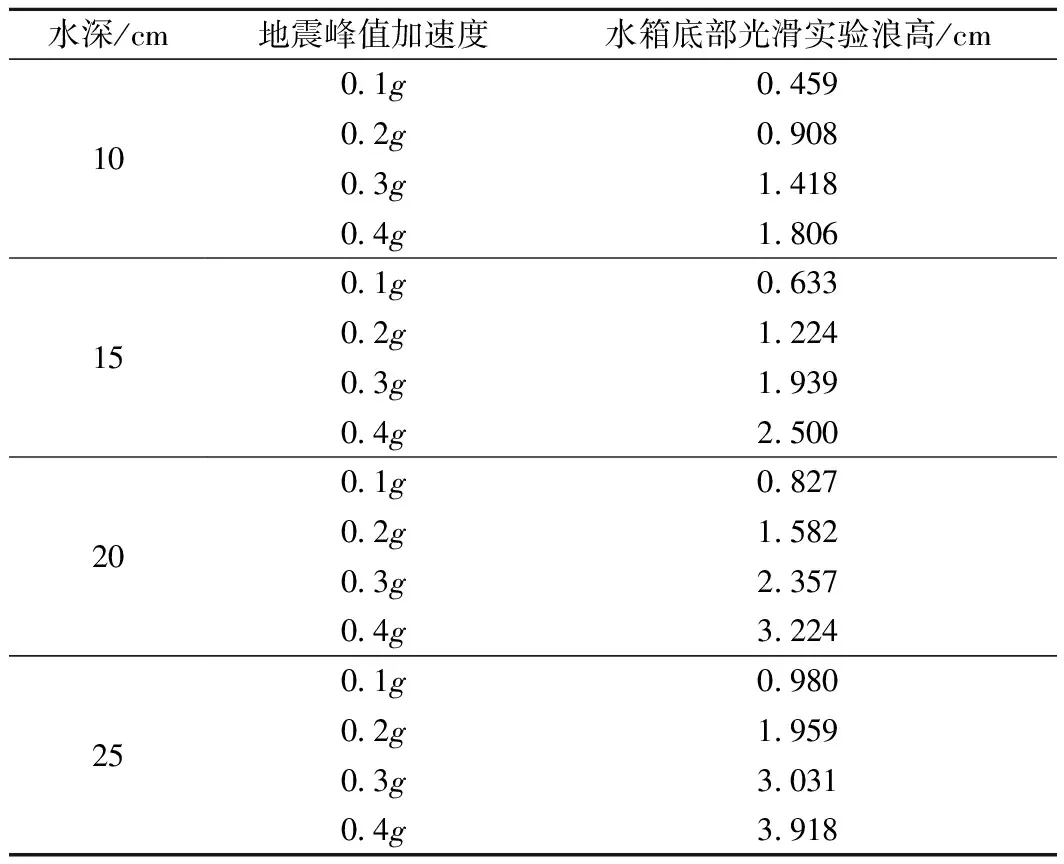
表3 实验结果

Demirel公式为

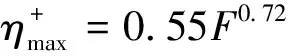
(1)

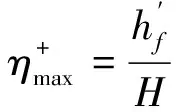
(2)

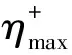
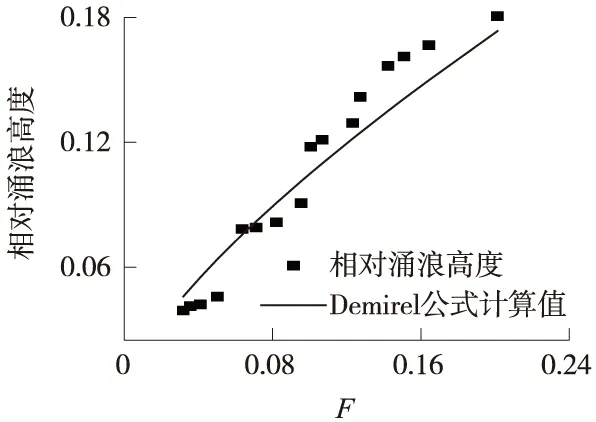
图5 实验数据与Demirel公式比对示意

由图5可知，Demirel公式值与振动台实验数据结果吻合良好。因此，认为该振动台造波模型的合理性得到了初步检验。

1.3 实验结果分析

(3)

式中，H为水深；h为地震涌浪最大高度；n为糙率。相关系数R为0.994。

现在不同水深条件下用式(3)与Demirel公式分别计算地震涌浪高度，并将计算值对比分析示于图6，计算中糙率取值为0.07。

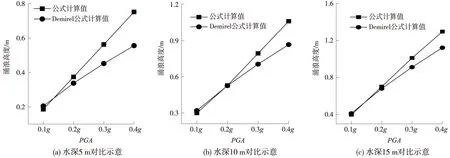
图6 不同水深下公式对比示意

通过图6可看出，当地震烈度在0.2g以下时，Demirel公式与公式(3)计算值接近；当地震烈度大于0.2g后，Demirel公式计算值小于公式(3)计算值，且其差值随地震峰值加速度的增加而增加。此外，对比上列3种水深的情况可知，当水深加大后，二者的计算值趋于接近。

2 冰碛堰塞湖溃决危险性评估

2.1 冰碛堰塞湖溃决危险性评估方法

漫溢型溃决是导致冰碛堰塞湖溃决的主要诱因，其机理为：当漫顶水流出现在冰碛堰塞湖的溢出口，并不断下切侵蚀溢出口，而在此过程中，由于溢出口被不断侵蚀，满溢水头高度上升，侵蚀作用不断加剧，当侵蚀超过一定阈值时，冰湖便会发生溃决，形成洪水。冰湖水面上升是导致溃决的导火索，水位超过溃决临界水深高度便具备了冲刷下切侵蚀冰湖溢出口的能力。对于溃决临界水深的高度，本文采用蒋忠信[19-20]建立的冰碛湖溃决的临界水深公式

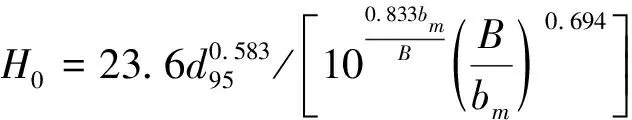
(4)

式中，H0为漫溢溃决临界水深；d95为冰碛物颗粒的最大粒径；B为终碛堤高度；bm为溃口平均宽度。

将公式(4)的计算结果小于涌浪高度作为判别冰碛堰塞湖溃决的依据。据此，提出地震涌浪作用下冰碛堰塞湖溃决危险性评估流程如图7所示。

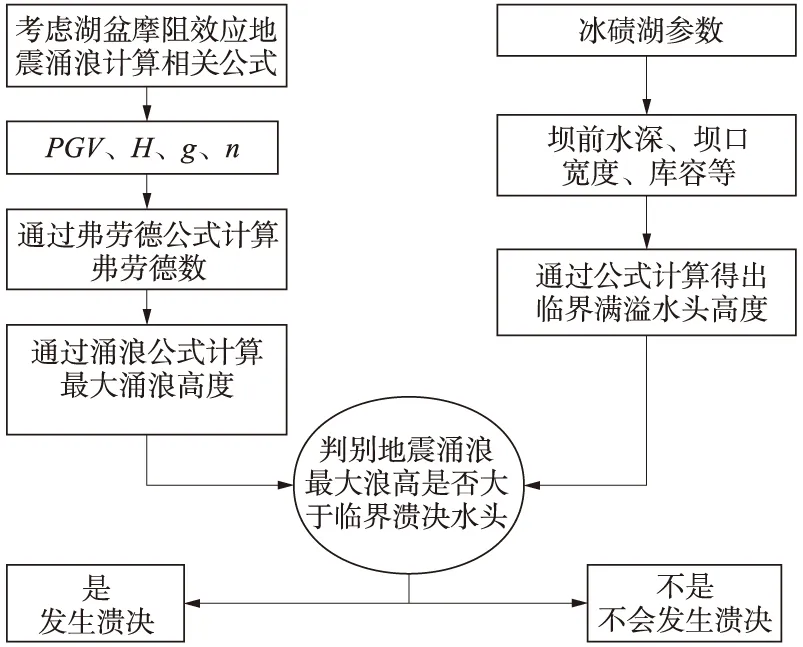
图7 冰碛堰塞湖溃决危险性评估流程

为对上述冰湖溃决危险性评估方法进行说明，现以川藏铁路沿线的光谢错冰湖为例进行案例计算。光谢错冰湖水深H=10.4 m，冰湖湖盆糙率n=0.07，地震动峰值速度取PGV=0.726 m/s。将上述参数代入公式(3)中，得到考虑湖盆摩阻效应的地震涌浪高度h=1.03 m；光谢错冰湖终碛堤长度B=320 m，溃口平均宽度为bm=21.8 m，d95取100 mm，将上述数据代入公式(4)得到光谢错的溃决临界水深为Hb=0.83 m。由于h>Hb，则判定光谢错冰湖会发生溃决。

2.2 川藏铁路帕隆藏布流域冰湖危险性评估

川藏铁路帕隆藏布流域冰湖分布密集，同时也是地震高烈度区，现按图7所示流程对该流域冰湖溃决危险性进行评估。根据全国第五代地震动峰值加速度区划图确定地震峰值加速度，地震动峰值速度则由通麦地震动加速度时程换算确定。分别采用Demirel公式与考虑湖盆摩阻效应的公式(3)，对该流域80个冰碛堰塞湖的地震涌浪高度进行计算，得到溃决危险性评判结果，见图8、图9。

对比图8与图9可以发现，当按Demrel公式计算涌浪高度时，仅有少数冰湖会发生溃决；而按公式(3)计算涌浪高度时，溃决冰湖数量显著增加。新增者水深均小于7.1 m，说明若忽略浅水冰湖的湖盆摩阻效应，可能导致不安全的评估结论。

图8 基于Demirel公式判别的危险冰湖分布

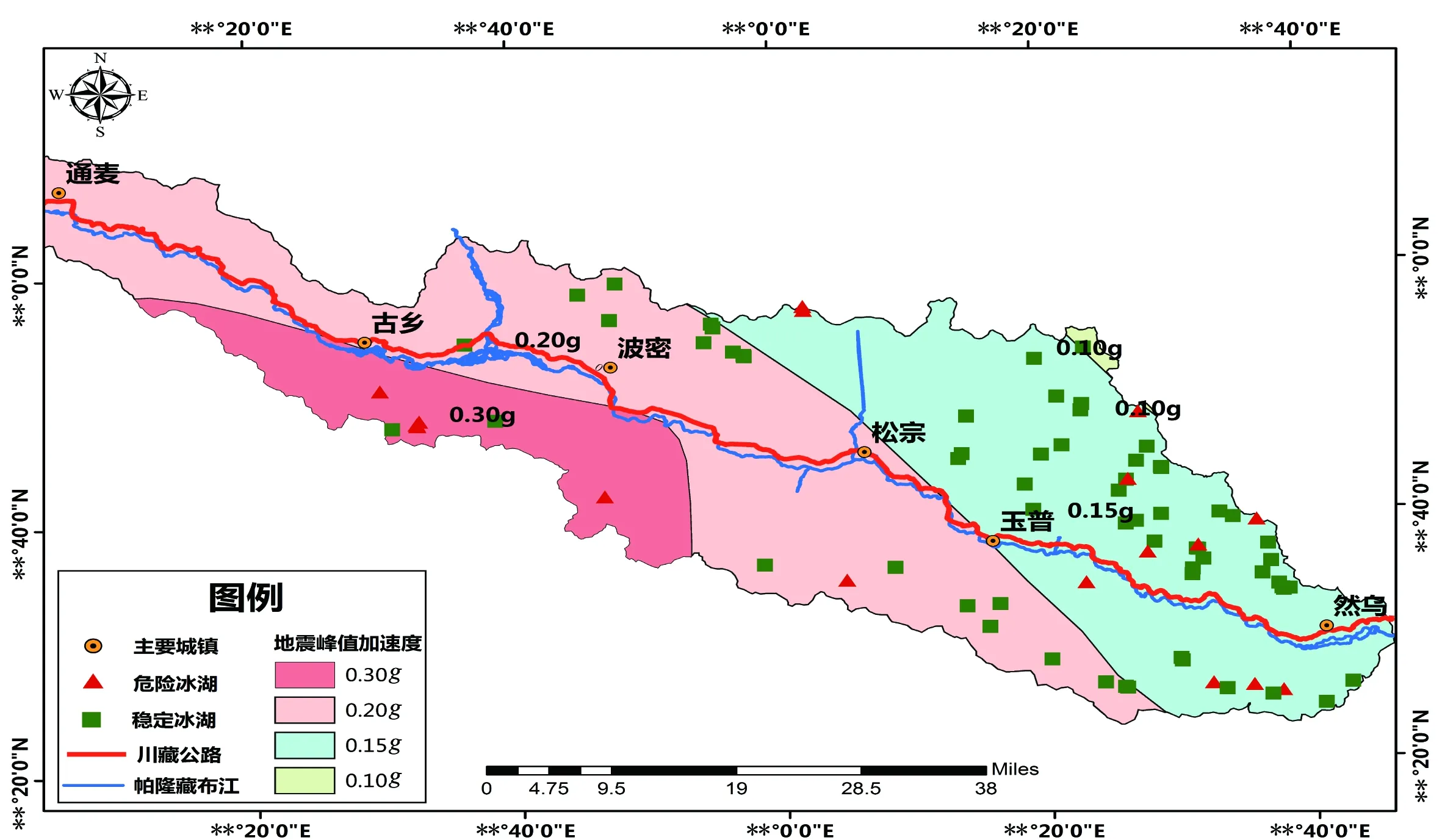
图9 考虑湖盆摩阻效应的危险冰湖分布

3 结论

通过进行大型振动台造波模型实验，获得并拟合地震涌浪实验数据，建立了考虑摩阻效应的地震涌浪计算公式；将公式(4)的计算结果小于涌浪高度作为地震涌浪作用下冰湖溃决的判据，然后以川藏铁路帕隆藏布流域的冰湖为例，对冰湖溃决危险性评估方法的应用进行说明，从而建立了一种与选线原则方案确定阶段精度要求相匹配的冰碛堰塞湖地震涌浪溃坝风险评估方法，主要结论如下。

(1)通过将本文公式与以高坝大库为研究对象的Demirel公式比较，分析二者计算值差距随地震峰值加速度、水深变化的特性，结合川藏铁路帕隆藏布流域冰湖溃决危险性评估结果，发现本文公式较Demirel公式对水深较浅的冰碛堰塞湖更具适用性，尤其是大震强震情况更偏安全。

(2)按照全国第五代地震动参数区划图，对帕隆藏布流域80个冰碛堰塞湖进行了溃决危险性分析。考虑湖盆摩阻效应时，具有溃决危险的冰碛堰塞湖数量显著增加，即对于川藏公路帕隆藏布流域的冰碛堰塞湖，若忽略其湖盆摩阻效应，可能导致不安全的评估结果。