一类dKdV方程的行波解分支
张会洋, 张克磊
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
非线性发展方程在物理学、化学以及光电子学等很多领域有十分广泛的应用,但是大多数人对该类方程的完全求解只能望而却步。人们很多情况下只能针对一些形式简单的特殊的非线性发展方程进行求解。KdV方程是一类很著名的非线性发展方程,对于其中经典的KdV方程很多学者给出了不同的求解方法,但是对于退化的KdV方程的研究相对较少。Rosenau和Hyman[1-2]引入退化Korteweg-de Vries(dKdV)型方程,研究其紧孤立波解的存在性。2018年,Zilburg和Rosenau[3]研究了一类dKdV方程:
∂tu+∂x(u∂x(u∂xu)+u2)=0
(1)
的孤立子的定性性质。最近,文献[4-7]采用动力系统分支理论[8-9]研究了几类非线性发展方程的行波解分支。目前,尚未有文献利用动力系统分支理论研究方程(1)的行波解分支。
采用动力系统分支理论对dKdV方程(1)进行分析研究。首先,对方程(1)进行行波变换u(x,t)=φ(x-ct)=φ(ξ),其中常数c为波速,将行波解代入式(1)可得:
-cφ′+(φ(φφ′)′+φ2)′=0。
(2)
对式(2)积分,积分常数记作g,则有
-cφ+φφ′2+φ2φ″+φ2=g。
(3)
方程(3)与下面的平面系统等价:
(4)
平面系统(4)存在奇异直线φ=0,利用dξ=φ2dτ对(4)进行变换,系统(4)变为正则系统:
(5)
系统(4)和(5)具有相同的Hamilton量:
(6)
其中h为常数。
首先利用定性理论中奇点的判别方法对系统(5)奇点的种类进行详细分析,并利用Maple绘制出系统(5)在不同参数(c,g)下对应的相图;然后求解出系统(1)的光滑孤立波解及周期尖波解的精确表达式。
1 系统相图分析
首先对系统(5)的平衡点性质及可能出现的相图进行分析。除了奇异直线φ=0之外,系统(4)的相图与系统(5)拓扑等价,所以通过分析系统(5)的相图即可得到系统(4)的相图。系统(5)的相图与参数(c,g)有关系,下面分析当参数(c,g)发生变化时,系统(5)奇点的种类以及个数。具体情况如下:




对系统(5)在不同参数(c,g)下求解得到的平衡点种类进行分析。假设系统(5)的线性化系统在奇点(φi,yi)处的系数矩阵记作M(φi,yi)。A=det(M(φi,yi)),det(M(φi,yi))表示矩阵M(φi,yi)的行列式,根据动力系统理论[8-10]可得:
1)当A<0,系统的奇点是鞍点;
2)当A>0且Trace(M(φi,yi))=0时,系统的奇点是中心;
3)当A=0且Poincaré指标为0时,系统的平衡点是尖点,否则为高阶奇点。
根据以上原理可得,系统(5)的原点为高阶奇点且位于奇异直线φ=0上。通过分析可得:Si(i=1,2,3,4)为鞍点;C2为尖点;Cj(j=1,3)为中心。参数(c,g)的变化决定系统奇点种类和相图也会发生相应的变化。
系统(5)在不同参数(c,g)情况下的拓扑相图如图1所示。
2 系统行波解求解
系统(5)的向量场在参数(c,g)下的轨线确定了系统(1)所有的行波解,下面对系统(1)相应的周期尖波解和光滑孤立波解的精确表达式。
2.1 周期尖波解
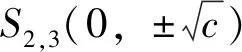
(7)
由式(7)和式(4)第一个方程可得到系统(1)的精确周期尖波解:
(8)

2.2 光滑孤立波解

(9)
由式(9)和式(4)第一个方程可得到系统(1)的精确光滑孤立波解为
u(x,t)=φ1-(φ1-φs)D。
(10)

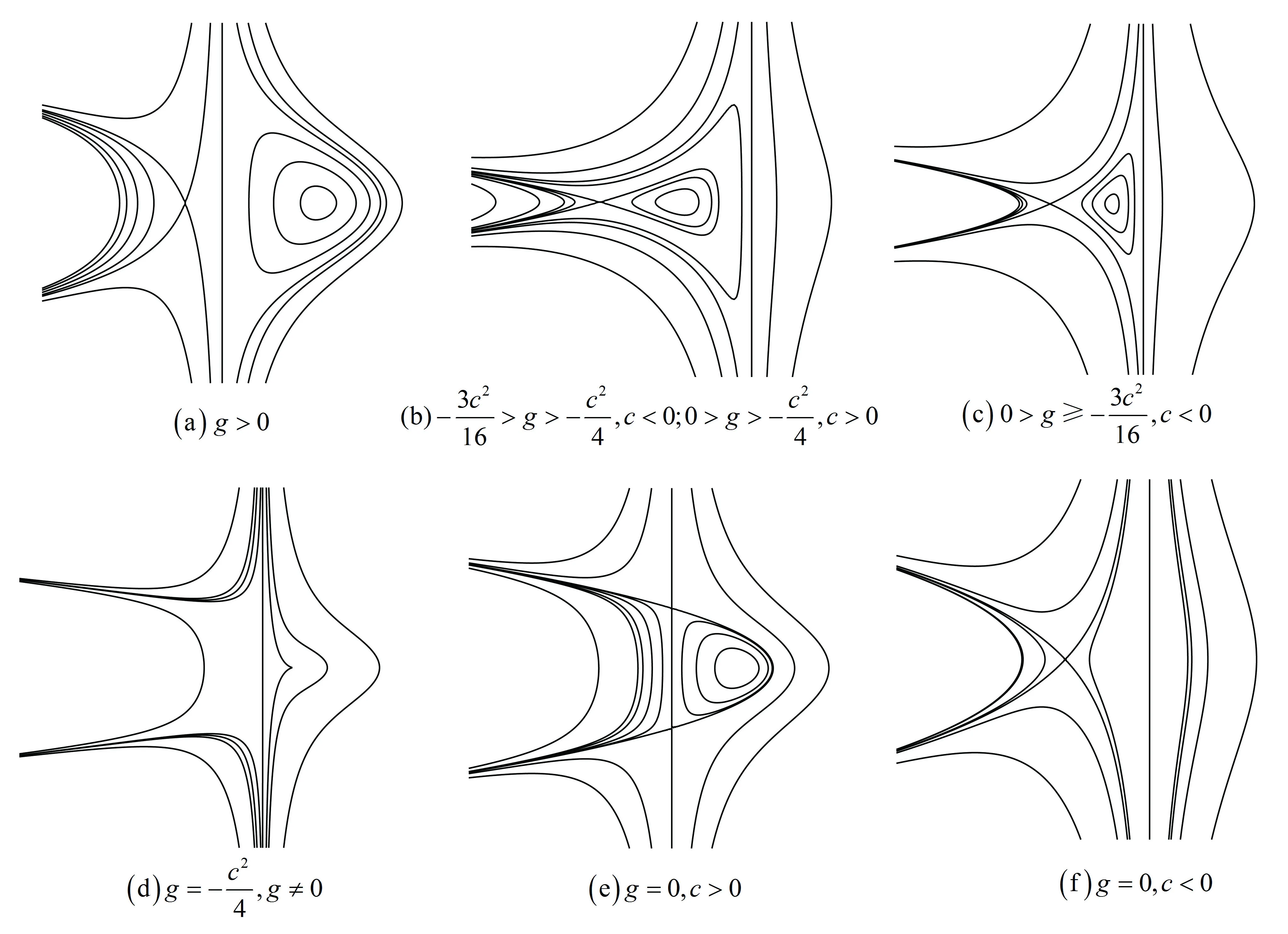
图1 系统(5)在参数(c,g)上的拓扑相图
通过式(8)和式(10)可得到系统(1)的精确周期尖波解和精确光滑孤立波解的图像,如图2所示。
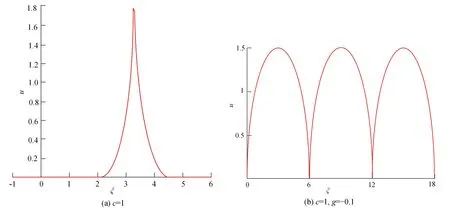
图2 系统(1)的周期尖波(a)和孤立波(b)
3 结束语
主要对一类退化KdV方程的行波解分支进行了分析。在分析的过程中,首先对系统(1)进行行波变换,然后根据定性理论分析这一类退化KdV方程的相图并求解出精确周期尖波解和精确光滑孤立波解,最后通过数值模拟给出周期尖波解和孤立尖波解的图像。

