Buck变换器数字控制器模拟化设计与离散化设计的性能比较

陈宇航，周诗颖，杨文铁，张 平

Buck变换器数字控制器模拟化设计与离散化设计的性能比较

陈宇航1，周诗颖2，杨文铁3，张 平2

（1. 海装驻葫芦岛地区军事代表室，辽宁葫芦岛 125004; 2. 武汉第二船舶设计研究所，武汉 430205；3. 海军工程大学，武汉 430033）

模拟化和直接离散化设计是数字控制器的两种经典设计方法。本文以Buck变换器为例，分别采用这两种设计方法对数字控制器进行设计，并对控制器的性能进行了对比分析。研究表明：数字控制器模拟化设计方法依赖采样周期，且离散化过程存在误差；直接离散化方法设计的数字控制器性能优于模拟化方法设计的控制器。最后，在MATLAB/Simulink中对上述分析结果进行了仿真验证。

数字控制器 Buck变换器 模拟化设计 直接离散化设计

0 引言

近年来，数字信号处理芯片随着性价比的不断提高而越来越多地被应用于电力电子装置上[1-3]。数字控制技术能显著降低控制系统的硬件设计，减少分立元件数量，改善系统可靠性，减低系统硬件成本；同时数字控制中不存在元器件的温漂和参数漂移等问题，调试成功后就能长期稳定运行[4, 5]。

但是，数字控制存在采样保持和量化过程，其系统与传统的连续系统有所区别，数字控制器的设计也有所不同。目前，数字控制器设计方法主要有两种，即模拟化设计方法和直接离散化设计方法，模拟化设计方法是先在连续域中设计控制器，然后用某种离散化方法对控制器进行离散化，直接离散化设计方法则是在离散域中直接建立被控对象的离散化模型，然后在离散域中直接设计控制器。因此，有必要研究这两种数字控制器设计方法及其性能差异。

为此，本文以船舶电源系统中常用的Buck变换器为设计实例，分别对其数字控制器进行了模拟化设计和直接离散化设计，并对两种设计方法进行了性能比较。最后，在MATLAB/Simulink中搭建了电路模型，对上述设计和分析结果进行了验证。

1 Buck变换器数学模型

Buck变换器[5]的电路图如图1所示。主电路由全控型开关管V、续流二极管、输出滤波器构成。其电路参数如表1所示。考虑调制器的调制波电压峰值V=5 V。

表1 Buck电路参数

图1 Buck变换器拓扑结构

通过交流小信号分析法[5-6]，可以得到Buck变换器的控制信号至电路输出的原始环路传递函数为：

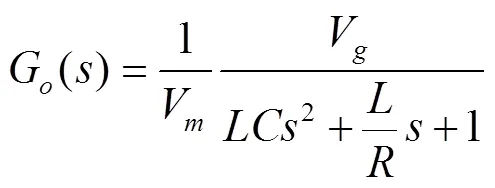
代入具体数值可得：

图2 Buck变换器原始环路开环传递函数波特图

进而，可以绘制出原始环路开环传递函数的波特图，如图2所示。

根据式(2)和图2，可知Buck变换器的原始环路开环传递函数存在重极点且无零点，幅频特性的转折频率为f1, p2=1/(2π0.50.5)=181.7 Hz。在低频段，G()的增益为26.1 dB，并在181.7 Hz处会有转折发生，其斜率为‒40 dB/dec，原始环路增益传递函数G()在830 Hz穿越0 dB线，相位裕度仅为7.18°。系统稳定裕度较小，必须设计补偿网络对系统进行校正，以确保系统稳定。

2 数字控制器的模拟化设计

数字控制器的模拟化设计步骤通常为：

1）在连续域中设计模拟控制器G()；

2）选择采样周期T;

3）选择合适的离散方法将模拟控制器离散得到G()；

4）验证系统的性能，若不满足性能要求，重新修改设计；

在本设计中，控制器将采用超前滞后矫正。为了保证控制器的快速性和不引入高频分量，工程上通常将补偿后的传递函数G()G()的穿越频率f设计为开关频率f的1/5~1/10。因此，本文取穿越频率为：

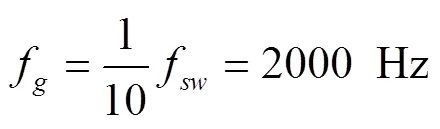
如果加入控制器后系统的环路增益函数幅频特性曲线以‒20 dB/dec斜率穿越0 dB线，那么系统将具有较好的相位裕度。为了得到‒20 dB/dec的斜率，控制器在穿越频率点必须提供+20 dB/dec的斜率。控制器G()利用两个零点来抵消原系统重极点影响，将两个零点频率设计为原始环路函数G()的两个相近极点频率的1/2，即：

如式(2)所示，G()没有零点。因此，为了改善系统的高频衰减能力，则可以将G()的两个极点设定为f3=f4=2f=40 kHz，以减小输出高频开关纹波。进而，可以得到控制器传递函数为：

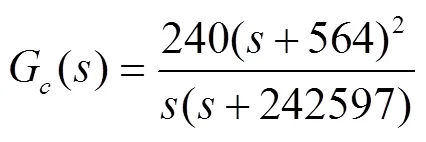
可以看出，加入控制器后，系统传递函数在4092 Hz处穿越0 dB线，相位裕度为82.8°，满足工程上的设计要求（即相位裕度>45°）。校正后系统的幅频特性得到改善，低频段有足够增益，高频衰减能力强，中频段也有足够相位裕度。

接下来，将对上述控制器进行离散化，并对常用的两种离散化方法进行对比分析。

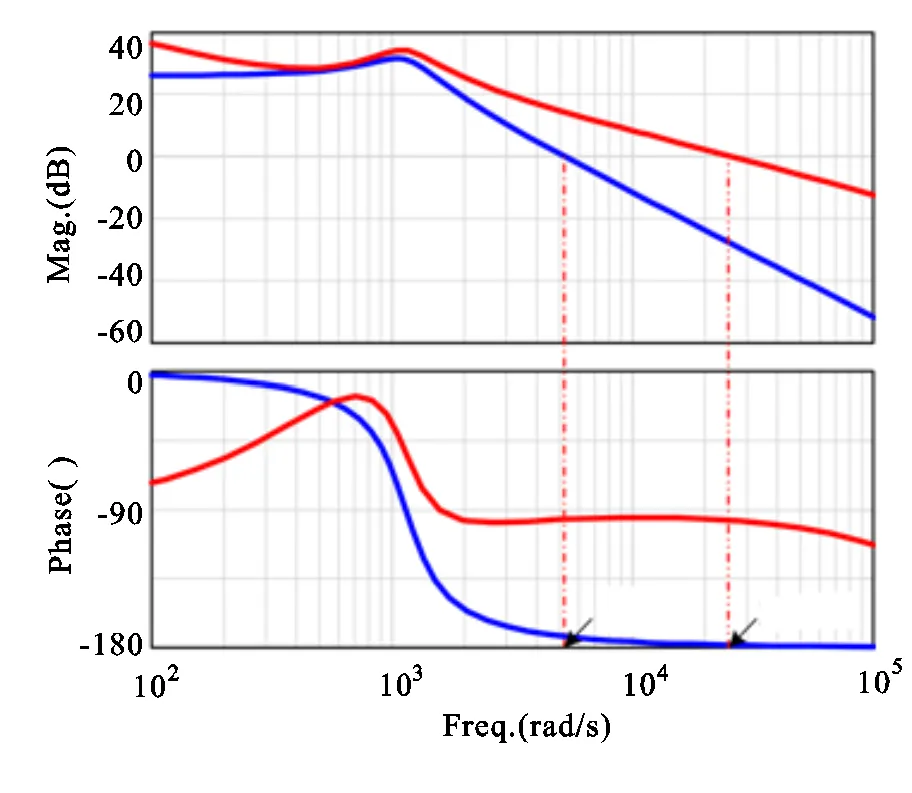
图3 加入控制器后系统的传递函数波特图

若采用Tustin变换法[7]，将G()离散后的控制器G1()可以表示为：

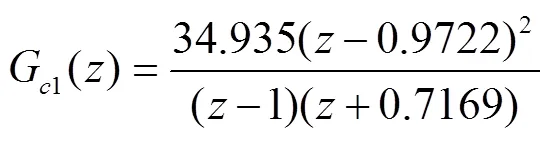
若采用零极点匹配法[7]，将G()离散后的控制器G2()可以表示为：

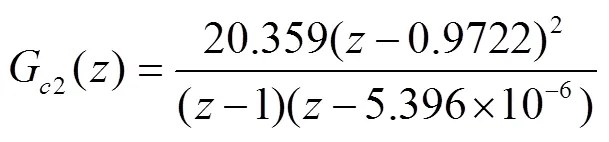
为了对比上述两种离散化方法的性能差异，在MATLAB中分别对在连续域中设计的控制器、Tustin离散化后的控制器G1()、零极点匹配法离散化后的控制器G2()进行单位阶跃响应仿真，其结果如图4所示。

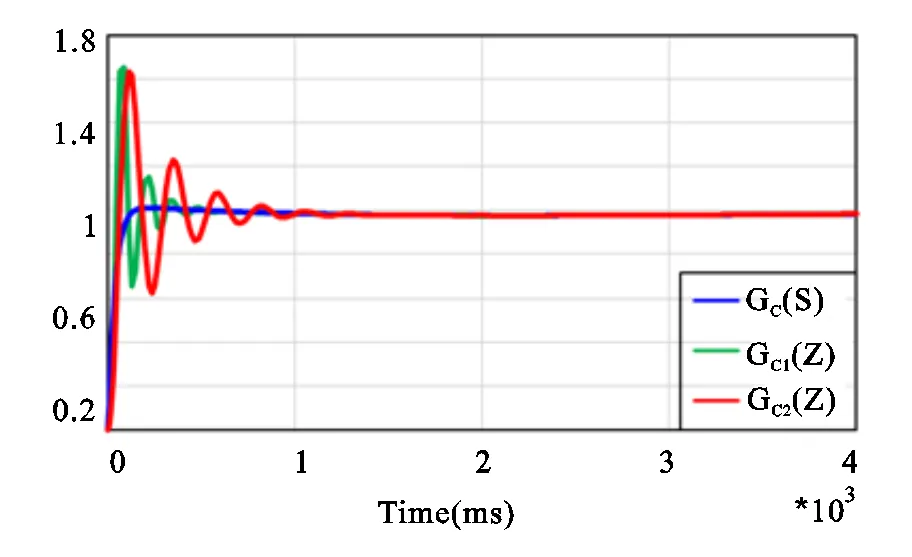
图4 连续域及两种离散化方法下系统的单位阶跃响应

可以看出：

1）采用连续域设计的控制器后，阶跃响应的超调量很小，调节时间仅为0.003 s，系统响应快速；

2）当连续域的控制器离散化后，系统调节时间差别很小，但是存在很大的超调量。其中，采用Tustin方法离散化后，超调量达65%；采用零极点匹配法离散化后，超调量达62%，远不满足工程上的设计要求；

模拟化设计的控制器再离散化受采样周期的影响较大，无法较为精确得到所预期的控制性能，为了确保系统控制的性能，避免离散化误差，需要进行直接离散化控制器设计。

3 数字控制器的直接离散化设计

数字控制器的直接离散化设计步骤通常为：

1）根据给定的系统性能指标，在平面上画出系统极点期望的允许区域；

2）求离散域中系统的开环传递函数G()；

3）仅为比例控制时，画出根轨迹；

4）设计离散域中的控制器G()，使闭环极点位于期望的区域；

5）验证系统的性能，若不满足性能要求，重新修改设计。

原始环路函数G()采用ZOH离散后，得到的广域脉冲传递函数为：

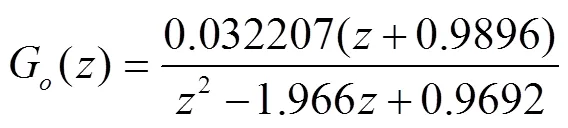
仅加入比例控制器时，假设比例增益为7，其根轨迹如图5所示。

可以看出，系统的零点为‒0.9896，有一对复数极点0.967±0.054j。零点和极点都非常接近单位圆，其根轨迹绝大部分位于单位圆之外，系统接近于临界稳定状态。需要根据根轨迹设计控制器，使闭环极点位于期望的区域，确保系统的稳定性。

这里给出系统控制性能指标：调节时间t<0.02s，上升时间t<0.001s，超调<15%，系统采样时间T=0.00005s。那么，有如下关系式：

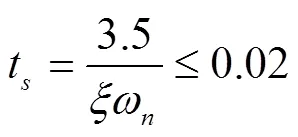
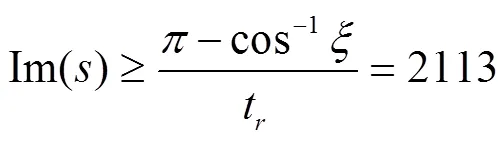
进而，可得期望中的根轨迹区域为对数螺旋线ξ≥0.517、同心圆R≤0.99和射线q≥6.06三者所围成的区域。

控制器的设计采用零极点对消法，将校正前系统的一对复数极点抵消，并在实轴上配置2个新的实数极点，为了使系统的稳态误差为0，校正后应增加系统的型别，即配置一个积分环节来改善低频特性，进而可将校正控制器的极点定为1，即增加一个1/(-1)项。然后，增加一个=0极点使得校正后的系统的根轨迹穿过期望的区域。由于原始环路中极点的虚部远小于实部，因此若将控制器的零点设计为0.967，则可抵消对象中极点的影响。最后，可以得到直接离散化设计的数字控制器为：

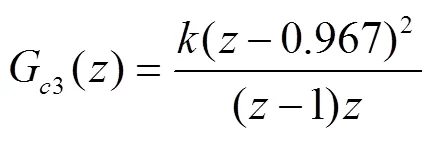
式中，为比例增益。

图6给出了加入控制器后传递函数的根轨迹。

图6 加入控制器后传递函数的根轨迹

可以看出，当比例增益取值为=7.89时，可以将闭环极点配置于期望的位置。由此可以得到直接离散化的控制器为：

图7给出了采用直接离散化设计方法时，系统的单位阶跃响应。

可以看出，当采用直接离散化方法来设计数字控制器时，系统的调节时间约为0.004 s，超调量约为10%，满足设计要求。并且与图4对比可知，其控制性能远优于模拟化设计的数字控制器。此外，可以看到，从设计的方法上来说，直接离散化设计方法更为灵活，不受采样时间对离散化的影响。

4 电路模型仿真

为了验证前述分析结果的正确性，在MATLAB/Simulink中搭建以图1所示Buck变换器的实际电路仿真模型，如图8所示。其中，输出电流I的控制指令给定为8A。

图8 电路仿真模型图

图9可以看出，采用直接离散化设计方法时，系统的输出电流调节时间约为0.005 s，并且几乎没有超调，电流纹波很小，满足设计要求。然而，模拟化设计后用Tustin离散化时，输出电流调节时间为0.012 s，超调量达10%；当采用零极点匹配法离散化后，输出电流调节时间为0.012 s，超调量达7.5%。由此可见，直接离散化设计的控制器性能优于模拟化设计的数字控制器。

5 结论

本文以Buck变换器为例，分别对其进行了模拟化和直接离散化的控制器设计，模拟化设计是在连续域中设计模拟控制器，然后将其离散得到等效的数字控制器。这种方法存在较大的离散化误差，受采样周期影响较大，控制效果较差。直接离散化设计采用了根轨迹校正的方法，将闭环极点直接配置在期望的区域内，不受采样周期的影响，其性能优于模拟化设计的数字控制器。本文对这两种设计方法分别进行了MATLAB/Simulink仿真对比，验证了理论分析的有效性。

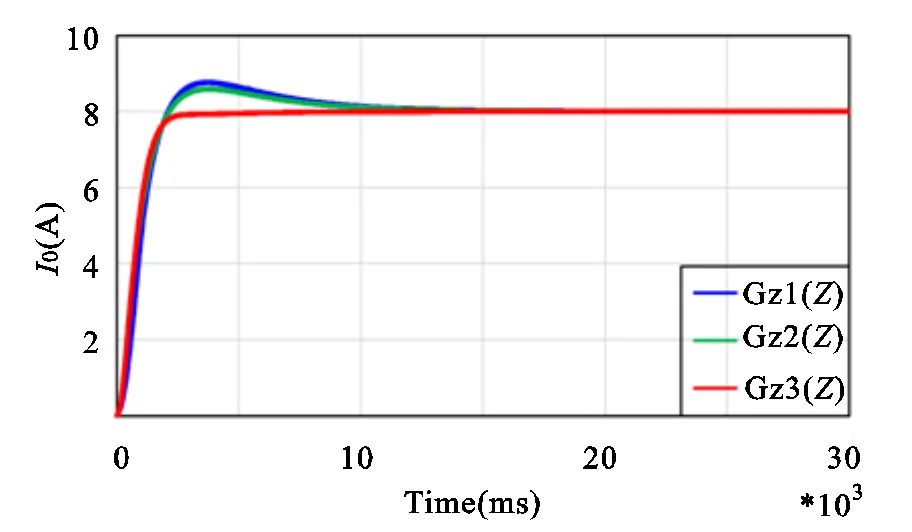
图9 不同数字控制器设计方法下的仿真波形图

[1] 刘健, 程红丽, 王立等. 电流跟踪数字控制的Buck DC-DC变换器[J]. 电工技术学报, 2011, 26(8): 50-56.

[2] Shi L, Lei W, Li Z, et al. Bilinear discrete-time modeling and stability analysis of the digitally controlled dual active bridge converter[J]. IEEE Transactions on Power Electronics, 2016, 32(11): 8787-8799.

[3] Eren S, Pahlevani M, Bakhshai A, et al. A digital current control technique for grid-connected AC/DC converters used for energy storage systems[J]. IEEE Transactions on Power Electronics, 2016, 32(5): 3970-3988.

[4] 高金源. 计算机控制系统[M]. 北京: 清华大学出版社, 2007: 128-177．

[5] 徐德鸿. 电力电子系统建模及控制[M]. 北京: 机械工业出版社, 2005: 95-109.

[6] 王英武，王俊峰等. DC/DC变换器小信号建模与补偿网络设计[J]. 电力电子技术, 2009, 43(3): 26-28.

[7] Yepes A G, Freijedo F D, Doval-Gandoy J, et al. Effects of discretization methods on the performance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.

Performance Comparison Between Analog Design and Discretization Design for Digital Controller of Buck Converter

Chen Yuhang1, Zhou Shiying2, Yang Wentie3, Zhang Ping2

(1. Naval Representative Office of Huludao, Huludao 125004, Liaoning, China; 2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China; 3. Naval University of Engineering, Wuhan 430033, China)

TM46

A

1003-4862（2019）11-0038-05

2019-09-04

陈宇航（1991-），男，工程师。研究方向：舰艇电力系统。E-mail: chen_yh316@126.com