指向核心素养的初中函数应用教学设计
潘金城 蔡雪梅

一、教材、学情与教法分析
在《义务教育数学课程标准(2011年版)》中明确指出“用函数解决问题”的目标:能结合图象对简单实际问题中的函数关系进行分析;能确定简单实际问题中函数自变量的取值范围,并会求出函数值;能用适当的函数表示法刻画简单实际问题中变量之间的关系。由此可见,实现目标的关键能力是:将实际问题抽象转化为数学问题,用函数的性质与图象分析去解决问题,根据实际问题的特征检验数学结论,从而形成建模思想。
“用一次函数解决问题”是初中数学(苏科版)首次运用函数知识解决实际问题的标志性内容,本节课包括两课时,第一课时的内容为“用一次函数的表达式解决问题”,第二课时的内容为“用一次函数的图象解决问题”。围绕学生进入初中后“用图象解决问题”的难点,笔者针对本课时,从教材、学情与教法进行如下分析。
1.教材分析
本节教材是一次函数图象在实际问题中的应用,就本节素材而言经历了“识图—用图—想图”三个活动,这三个活动的功能各异,活动一重在识图,在实际的情境中理解“上升快慢的实际意义”和探索“正确决策方法”,理解交点意思;活动二重在用图,自主建构“一次函数”数学模型,借助图象分析两种运输方案的优劣,发现交点意义,体验图象在解决实际问题时的应用;活动三重在想图,让学生感受不同走势“折线段”的意蕴,感悟到数与形的内在联系,更深刻理解模型思想。
2.学情分析
学生已经知道一次函数的概念与性质,也会能运用方程模型解决简单的实际问题,但运用一次函数的知识解决实际问题尚属首次,特别是同一坐标系内不同图象之间的区别是学生理解的难点,可能存在三个方面的困惑:其一,不清楚“上升的快慢”与一次函数y=kx+b(k≠0)中的“k”之间的关系;其二,不清楚“图象的交点坐标”与“函数表达式”之间的关系;其三,不清楚“折线的意义”与“实际问题”之间的对应关系。每个困惑都体现着“抽象”“建模”等数学基本思想。
3.教法分析
因为一次函数学习的目的是为了解决实际问题,所以本节课的教学重点是在实际问题中认识图象和应用图象,更好地感悟数与形的内在联系;由于一次函数图象的陡峭程度反映因变量与自变量之间在一定范围内的变化情况,视觉上的关注要从点向线转变,但又要回归到线上的观念点分析陡峭程度的实际意义,因此图象的走势所对应的实际意义是学生学习的难点。基于教学的重难点,本节课采用“问题情境—建立模型—求解验证”的教学方法,初步学会从数学的角度发现问题和提出问题,综合运用数学知识解决简单实际问题,增强应用意识,提高实践能力。
基于以上分析,确定如下素养目标:
(1)能根据实际问题中变量之间的关系,确定一次函数的表达式,通过用一次函数表述数量变化及其关系的过程,体会模型思想。
(2)能用一次函数解决简单实际问题,在此过程中,感悟数学具有抽象性、严谨性和应用的广泛性,体会数学的价值。
(3)经历“问题情境—建立模型—求解验证”的数学活动,初步学会从数学的角度发现问题和提出问题,综合运用数学知识解决简单实际问题,增强应用意识,提高实践能力。
二、教学案例简要设计
1.自主尝试,认识图象
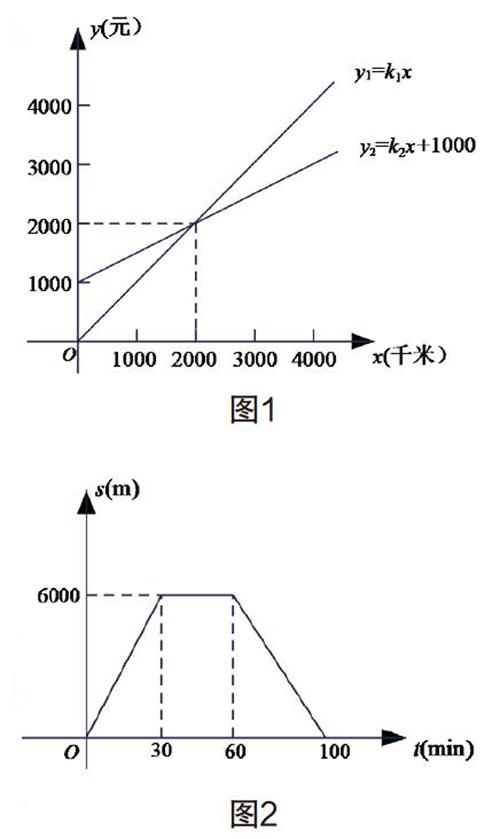
问题1:元旦将至,小明的爸爸准备租车外出旅游,从甲、乙两家出租汽车公司收取的租车费y1(元)、y2(元)都是用车里程x(千米)的函数,它们的图象如图1.
(1)请写出这两个函数图象的共同点与不同点.
(2)若用车里程为1000千米,选用哪家出租汽车公司?
(3)用车里程为多少時,乙公司的租车费用比甲公司少?
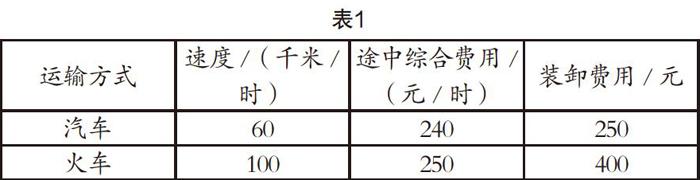
问题2:小明的爸爸骑车从家出发到某出租汽车公司洽谈租车事宜,他离家的路程s(km)与出发的时间t(min)之间的关系如图2所示,请回答问题。
(1)出租汽车公司离家______km;
(2)小明爸爸在出租汽车公司停留了______min;
(3)小明爸爸回家时的速度为______km/min;
(4)若小明在爸爸离家30min后出发匀速骑车迎接爸爸回家,当他出发35min时恰好遇到回家路上的爸爸,请在所给的坐标系中画出小明这段时间离家路程与爸爸出发时间之间的函数图象;
(5) 小明骑车的速度______爸爸前往租车公司时速度。(填“<”“>”或“=”)
【设计意图】遵循简单、根本、开放的原则设计了一道开放性的问题1,在实际情境下,通过“数”与“形”的对应关系理解点所表示的实际意义,感受线的陡峭程度所表示的实际意义。
2.建立模型,运用图象
问题3:某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参考数据如表1所示。
(1)请分别写出汽车、火车运输的总费用y1(元)、y2(元)与运输路程x(千米)之间的函数关系;
(2)你认为用哪种运输方式较好?
拓展:若另一辆汽车沿着高速公路把一批新鲜蔬菜运往外地,其参考数据如表2所示。
问题:当运输里程数满足什么条件时选择在高速公路上的运输方式?
【设计意图】问题3(2)中,解决策略的选择不唯一,让不同理解水平的学生有不同的解法,但拓展题的解决更能体现图象法的优越性,突出本节课教学的重难点。
3.构造情境,展想图象
问题4: 根据图3中的函数图象,说出x,y变化过程的实际意义,线段AB与x轴平行,点C在x轴上.(要求自己给出数据,自主设计问题情境)
【设计意图】 看图说话可培养学生的发散思维,编拟实际问题是对前面问题的逆向思考,也是数学建模素养培育的重要方式。
4.课堂小结,慧悟图象(略)
三、案例设计的三个视角
在《素养何以在课堂中生长》一书中指出,提出问题、建立联系和个性化表达是学生的关键能力,这与史宁中教授对数学教学的素养目标划分是一致的,这三个关键能力的表述是素养目标的显性表达,现从自然、开放、自主的三个视角来培养学生的关键能力。
1.自然性视角——素养生长的路径
美国教育心理学博士伯尼斯。麦卡锡以提供教学指导为目的,借助四个象限提出完整的自然学习过程——学习循环圈,包括“为什么”“是什么”“应怎样”和“该是否”四个象限(如图4)。学习循环圈让我们的教学设计更能从知识的结构规律关注知识从哪里来?到哪里去?怎么去? 更能从学生的认知规律经历“感知、理解、记忆和应用”的过程,让知识生长可视化。
本章的内容结构包括:概念、图象与性质、应用、图象法解方程、不等式等;本节课的前一课是将实际问题转化为一次函数,主要运用函数关系式,通过方程、不等式建立之间的联系,由于函数具有“数与形”的二重性,两者之间“形异实同”“辩证统一”“浑然一体”,“由数想形”,这是知识生长的基础。其知识结构如图5。
通过上图,我们不难感受到用图象法解决问题的策略不是从天而降的,它基于函数关系式、方程不等式等知识,函数图象只不过是它更为直观的表达形式, “形”与“数”的一一对应顺应了学生认知,知识的来龙去脉更为清晰,“图上作业法”的提出便顺其自然。
2.开放性视角——素养发展的抓手
开放原意是释放、思想开通、解放等。在数学教学中的开放是指教学的组织形式多样,思维方式多元,设问方式多角度。在本节课的三个研学环节中,都体现着开放式教学。
“认识图象”环节中,让学生写出两个图象的异同之处,体现了简单、根本、开放的基本原则,视角不同获得的结论也不一样。如从图象的形状看,它们都是射线;从公共点的意义看,表示里程数为2000km时所租车费用相等;从走势看,随着里程数的增加租车费用也增加……不同点选择的视角可以更多,如射线的端点不同,表示起租费不等;上升的速度不同,说明比例系数k不等;位置的高低不同,表示相同的里程数租车的费用不等……在“运用图象”环节中也体现着开放的教学,方法的选择不限于图象法,两种方法两个视角,通过解法的开放,让两种方法相互联系,交相辉映。在“展想图象”这一环节,更是具有开放性,一图多景,各美其美,美美与共,但表示同一种图象。
设问开放,让学生有話可讲,让学生的思维在与文本对话、与同伴和师生对话、与自我对话交流中动起来,对待学生的回答多予以鼓励,用开放的设问、开放的表达、开放的展示和开放的胸怀让学生产生思考,激活思维,感悟思想。
3.自主性视角——素养升华的基础
自主学习是指个体在生活过程中通过获得直接或间接经验(知识)而产生的行为或思想上的相对持久的变化,学习是一个循序渐进、由浅入深、深入浅出的过程。
教的秘诀在于度,学的真谛在于悟。“悟得”是指通过思与觉,内化所学内容成为自己智慧的一部分,从而使自己的价值层面得到改变的过程。知识是外在于人的,是一种可以量化的“知道”,只有在悟的过程中,让知识进入人的认知本体,悟有所得,才能称为素养。“悟得”是一种意义理解,是一种规律性的认识,是一种智慧。
“悟得”的过程是深度的自主学习的过程,自主是合作的前提,是探究的基础。在“认识图象”环节中,展示交流后让学生自主反思“意、数、形”之间的对应关系,自觉领悟“数形结合”的思想。在“运用图象”环节中,从列式、画图、比较等活动引导学生自主建构“一次函数”数学模型,在拓展环节中更是让学生独立思考后体悟图象法的优越性。在“展想图象”环节中也不忘让学生自主思考图象的意义,整个过程就是学生从“习得”到“悟得”的过程。
由上分析,我认为“悟得”是素养提升的重要标志,是自主学习的高级表现。
四、案例中数学素养的分析
基于自然、开放、自主的三个视角设计指向核心素养的案例,是否能反映出不同层次的数学素养成分,达成数学素养目标?我们从两个方面进行分析。
1.素养成分与素养目标的关联分析
指向数学核心素养的教学不仅体现着数学素养的成分,而且与素养目标有着高度的关联。就本节课而言,研学的每一环节都体现着数学核心素养,如表3所示。
2.素养水平与素养成分的关系分析
喻平教授将数学核心素养的水平划分为知识理解、知识迁移和知识创新三个层次,所涉及的素养水平分析如表4(知识理解-1,知识迁移-2,知识创新-3)所示。
通过以上分析,我们不难发现,以自然、开放、自主的视角设计的教学能更多地指向数学核心素养的目标与内涵,能更好地体现不同水平的数学素养。因为自然而遵循规律,因为开放而体现层次,因为自主而保障效能,所以自然、开放、自主是基于教材、学情、教法的一个整体的表达,是教师聚焦素养进行教学设计的有效视角。
(本文系“江苏省十三五规划课题:基于核心素养的GBR课程建设”阶段性成果。)
【参考文献】
[1]喻平.基于核心素养的高中数学课程标准与学业评价[J].课程·教材·教法,2018(1):80-85.
[2]潘金城.基于核心素养的“反比例函数图象”教学[J].教育研究与评论,2017(9):79-85.

