壳壁热斑模型及其热应力计算近似方法
(茂名重力石化装备股份公司,广东茂名 525024)
0 引言
机件缓慢的加热过程有足够的时间与周边环境进行热交换而保持其温度不变,这是一个等温过程,快速加热过程则与绝热过程对应,这种情形下物体来不及与外界进行热交换,变形过程就已经完成。承压设备在装置开停车中经历介质的变温过程,在正常的控制下可近似为等温过程。文献[1-2]中研究了内压厚壁圆筒体最大允许内外壁温差,结果表明,在GB 150—1998《钢制压力容器》规定的设计压力下,对于大多数在高温下工作有保温层的厚壁圆筒能够满足强度要求,当超过相应的最大允许内外壁温差时,需要对内压引起的应力和温差引起热应力的组合应力进行强度校核计算。与此有别的是,工程实际中,各种承压设备从产品制造到安装运行或者非正常工况会存在一些界于等温过程和绝热过程之间的情况,特别是由壳壁局部区域温差引起的热应力,复杂的热应力会引起变形,影响密封,还有因局部超温开裂失效的现象。
1 热斑现象及其概念
1.1 热斑现象
设备制造中焊接一个临时吊耳,或者构件组对时的点焊都属于瞬间加热,是一种局部集中的焊接热行为,为了避免这种激烈的焊接热产生开裂,有时需要在壳体上的相应位置一定范围持续预热;厂房屋顶漏雨对其下面正在焊接或热处理中高温壳壁也会产生强烈的冷击;冬天在室外使用电动高速砂轮机对高强钢实施瞬间的强力修磨,则会先后产生急热和急冷现象。这些都是设备制造中典型的局部变温现象。
石油化工设备运行中,某些高温介质使进料口周边或者对面受到冲击的局部壳壁温度升高。换热器管箱的介质进口与圆筒短节偏心连接时,或者换热器进料管是一个90°急弯弯头结构时,都可能由于偏流引起局部壳壁温度梯度;石油化工环氧乙烷装置、苯乙烯装置等大型反应器与石油炼制加氢裂化反应器、催化重整装置反应器相比,设置较多的热电偶,用于监控催化剂或流介问题引起的不均匀局部变温;乙烯裂解气夹套管式急冷废热锅炉因集箱分配给诸多夹套的偏流以及夹套进口的激变流态会造成夹套局部流量减少,引起局部管壁高温鼓包;锅炉高温高压蒸汽出口管路上与其垂直连接安装的减温器在紧急运行中也很容易在蒸汽管上形成局部的相对强冷;炼油厂常减压装置顶部普遍采用“一脱三注”的防腐措施,注入介质与原油之间的温差以及频繁的间歇注入操作,使得注入小管在主体大管上形成相对低温的冷斑,有的结构连接处热疲劳开裂。
电力装置也像某些石化装置那样存在开机短时高温或运行串温等瞬时高温现象,例如,点火风道的开机短时高温,因此在其膨胀节设计时要考虑略短高温工况,提高膨胀节的可靠性[3]。某电厂1 000 MW超超临界火电机组再热段管道疏水罐在运行不到2年时出现罐体开裂,原因是再热管道上的冷凝水反复回流,造成罐体上下部分温差较大,从而产生热疲劳裂纹扩展所致;压水堆芯热电偶贯穿反应堆顶盖的密封失效也会引起连接处类似的壳壁局部高温问题[4]。
设备失效分析中发现,某厂原来设计的储罐,其夹套内介质原为30~50 ℃热水,改用蒸汽代替热水作为加热介质后,夹套进口附近局部温度较高,导致结构出现裂纹;加热炉作为一种特殊的换热设备,其辐射炉管常见的鼓包变形无论是塑性变形或蠕变,大多是局部高温作用的结果[5];美国Great Lakes Carbon公司研究认为,焦碳塔生焦阶段的气分在焦层形成过程中存在无规则流动并构造出一些类似中间的树干向四周扩展的树支状通道,见图1[6],冷焦操作阶段的冷水会沿着这些通道窜至高温塔壁,引起局部壳壁温度的瞬态变化;Ju等[7]基于采用软件有限元分析对焦炭塔在热和机械载荷作用下进行弹塑性应力分析时发现,焦炭塔在工作过程中出现的冷热点会引起显著的应力,从而导致塔体变形。
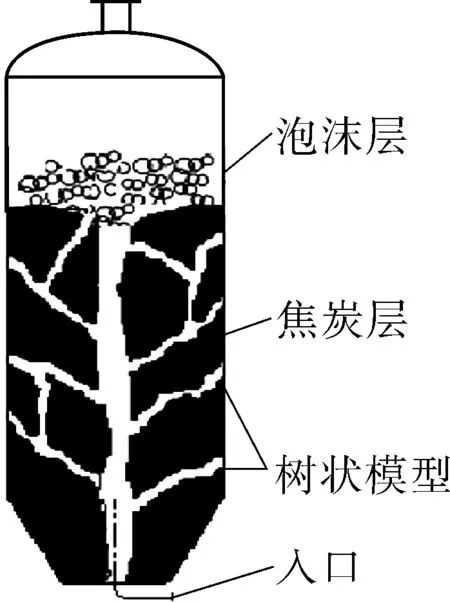
图1 焦炭塔焦床树支通道
某化工公司用于煤焦油加氢制油的加氢反应器于2008年投料试运行,仅运行9天就发生底部封头与筒体连接的环焊缝处开裂起火事故,调查发现,在事故发生前该反应器出口温度有缓慢升高趋势,加大通入冷氢后出口温度上升情况未能有效控制,直至超过正常温度,随后底部封头上发生显著变形开裂事故,如图2所示。可以推断,在该事故中,如果裂口正对有相邻的压力容器,则后者迎火一侧也承受局部高温的作用。

图2 封头局部开裂示意
设备研究中,2015年12月,在南京航空航天大学举行的第一届全国热应力大会上,清华大学冯雪教授以“热冲击下材料动态应力演化与裂纹扩展”为题作了大会报告,介绍了动态应力对裂纹扩展的影响;文献[8]中对临界热通量下反应堆压力容器的极限承载能力进行研究,鉴于熔融物堆内滞留已成为核电厂处理堆芯熔融严重事故的一种有效管理策略,为使熔融物堆内滞留成功,既要满足热失效准则,保证反应堆压力容器的局部热通量低于堆腔内冷却剂的临界热通量,也要确保反应堆压力容器的压力边界完整性,避免发生结构失效,为此对临界热通量下某堆型的反应堆压力容器进行热分析,得到了反应堆压力容器器壁局部熔化后的有效几何模型和沿壁厚的温度分布,再考虑热载荷和压力载荷作用,对该反应堆压力容器模型进行极限载荷分析和熔融物堆内滞留72 h蠕变分析,最终确定反应堆压力容器的极限承载能力。
热斑和冷斑以多种形式存在于石油化工、电力等诸多行业装置的建造和运行过程。前面列举了一些直观的工程现象,热斑除了可以由对流或辐射引起,也可以由强烈摩擦引起;除了可以通过流介传热,也可以由连接件传热;除了常见于壳体的内壁或者外壁,也不排除厚壁中的缺陷作为热阻因素在壁内埋藏热斑。此外,热斑也具有正面作用,热聚焦可以加热或点火,摩擦焊接或火焰切割都是科学利用热斑的例子。
由此可见,关于非正常或不期望的局部热斑是客观存在的,其相关的工程现象已引起个别关注,但是还未形成一个引起业内普遍认识的专题,有关研究深浅不一,大多数都不够具体深入,尚未见热斑模型及其热应力计算方法的报道。
1.2 热斑应力与热点应力的区别
ASME Section Ⅲ,Divisions 1—2013的NB-3213.13小节指出,在确定许用应力时,视引起变形的容积或者面积状况,应考虑两种热应力,其中一种局部热应力是由于热膨胀差完全受到限制而没有明显的变形,在疲劳分析时将其归类为峰值应力。评估的局部热应力包括:壳壁中小热斑的应力(the stress in a small hot spot in a vessel wall);实际应力与圆筒壳径向温度分布引起的等效线性应力之差;复层材料与基层材料之间由于膨胀系数差异引起的热应力。文献[9-10]中指出,ASME规范疲劳设计分析方法用到的应力类型也包括热点应力(hot spot stress),是指通过外推得到的、位于裂纹潜在萌生区的应力,如图3所示。

图3 应力类型及其位置示意
显然,同在ASME规范中,这两处都用到了hot spot一词,但是笔者认为“the stress in a small hot spot”与热点应力(hot spot stress)是不同意思的两个表达,容易被读者混淆为同一意义。这里的热点应力本意指“关注点”的应力、“研究讨论点”的应力或者“焦点”应力,实质还是结构应力,这里的热点应力与热应力或点应力的概念也有很大的区别,是疲劳分析中的概念。为了提示区别,有的报道就在疲劳分析中的热点应力名词上加上引号,即“热点”应力[11]。
在中文里为了准确表达这两个不同的概念,可采用与热点应力相区别的另一个概念——热斑应力,这样做的工程背景既涉及承压设备制造、运行、失效及研究中各种与局部变温有关的案例,也包括专业技术上精细分类、深入研究的需要。而且,鉴于文献[9-10]中已将“hot spot stress”一词翻译为热点应力,笔者认为应把热斑应力对应的词组翻译为“thermal spot stress”,以免混淆。
1.3 冷斑应力与广义热斑应力
在承压设备事故现场救灾中,被消防水柱急冷的高温壳壁也会受到局部降温的作用。炼油加氢反应器内局部突变高温的控制中,加大引入冷氢流量作为调温手段之一,如果操作不当,局部壳壁受到冷氢的急冷作用,内壁堆焊的防腐衬里出现与基体的剥离现象;核装置事故工况中的紧急压水或气冷操作不当也会引起结构局部温度急降。这类事故在壳壁中引起的局部区域温度突然明显降低,称之为冷斑,由此引起的应力称为冷斑应力。虽然温斑作为一个中性词,在概念上可以包括热斑和冷斑,但是,以广义热斑应力作为包括热斑应力和冷斑应力的概念,更符合业内的传统。
不过,热斑膨胀中承受周边主体压缩的能力要强于冷斑收缩中由周边主体拉伸的作用力,从而使冷斑更危险。据介绍,李冰父子主持修建都江堰时,通过柴火烧热岩石后浇灌冷水致其开裂,才形成工程中关键的“鱼嘴”,这个世界文化遗产的建造工法就包含冷斑应力的原理。
1.4 热斑的形态
笔者的理解,前述热点应力中的“点”显然指的是结构表面的一个点,是几何位置上的一个点。而热斑应力中的“斑”在结构表面上几何形状是一个小的圆形范围的区域,在结构内指的则是表面温度较高的“斑”沿壁厚传热形成一个立体的小区域。换句话说,热斑应力是结构内一个立体小区域的温度高于其周边温度,其热膨胀受到周边的约束所引起的应力,实质是温差应力,而不是ASME规范的热点应力所属的结构应力。温差应力的大小当然与温差有关,而温差的测定则与测温点的间距有关。
2 热斑模型
2.1 局部热载荷作用范围对其效果的影响
(1)对前人成果的认识。
为了确定金属表面温差波动的有效次数,JB 4732—1995(2005年确认)的3.10.2.1条中对于回转壳的经线方向以及平板上的表面温差的测定间距分别提出计算式[12]:
(1)
L=3.5a
(2)
式中L——两相邻点之间的最小距离,mm;
R——垂直于表面从壳体中面到回转轴的半径,mm;
δ——所考虑点处部件的厚度,mm;
a——板内加热面积或热点(笔者在文中称之为热斑)的半径,mm。
JB 4732—1995(2005年确认)中没有给出半径a的确定方法,为了加深对上述两式、特别是半径a的认识,将式(1)转化为:
(3)
再将式(3)与式(2)比较,得到圆筒体尺寸与其等效视为平板时热斑半径的关系式:
(4)
根据上式绘制曲线如图4所示。可以看出,各区线曲率不大,热斑半径a随着筒体半径R或者筒体壁厚δ的增大而增大。
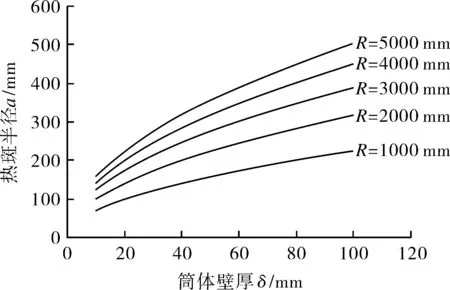
图4 圆筒体的等效热斑半径
(2)集中载荷的应力分布区域。
文献[13]中注意到了集中载荷作用于平板上的应力分布现象,并指出当受载半径趋于零时,受载面积趋于小面积, 所计算载荷除以小面积计算所得的最大应力都呈现非常大的数值;更精确的分析表明,计算集中载荷在半径为r的小面积上实际产生的最大应力时,可用所谓的等效半径r′代替r,这个半径主要决定于平板的厚度δ,其次取决于最小横向尺寸。Holl[14]分析了r′如何随着平板宽度变化的关系,Westergaard[15]给出了等效半径的近似表达式:
(5)
此式适用于任何形状的板,可以应用于所有r<0.5δ的情况,当r较大时可以使用实际的r。使用等效半径使得计算(名义)点载荷产生的有限最大应力成为可能,这与常用公式表明这些应力为无限大不同。
式(5)的推导过程未见报导,为了加深认识,笔者根据上式绘制成曲线(见图5)进行分析,可以看出,当载荷半径r较小时,等效半径r′随着平板厚度的增大而略有增大;但当载荷半径r较大时,等效半径r′随着平板厚度的增大反而略有缩小;总体上反映了平板厚度影响等效半径的一种性质变化或者不确定性。

图5 最大应力的等效半径
再绘制曲线(见图6)进一步分析。如果粗略地将应力理解为载荷与其作用面积之比,则图6中载荷半径与等效半径的圆形面积之比可以间接地反映应力之比,还反映该比率随平板厚度的变化。当载荷半径r较小时,面积比(应力比)随着平板厚度的增大而显著减小,也即厚板计算得的等效半径显著增大;当载荷半径r增大时,面积比(应力比)随着平板厚度的增大而表现出先上升、然后很快下降;当载荷半径r再增大时,面积比(应力比)随着平板厚度的增大而倾向于只上升,而没有下降;最后,载荷半径r的进一步增大,面积比(应力比)随着平板厚度的增大而线性上升,但是关系直线的斜率逐渐降低,平板厚度的影响减弱。总体上也反映了平板厚度影响应力比率的不确定性变化。

图6 平板厚度及受载半径对圆形面积比率的影响
由此可见,除了热斑及其应力的概念需要明确,关于热斑的模型及其尺寸大小(即作用范围)也值得研究,这些都是热斑应力计算的定量基础。
2.2 热斑基本模型及尺寸
上述分析中只基于壳体壁面方向温差,不考虑壁厚存在温差,实际上薄壁很容易热传导透过整个壁厚,所以这里研究的对象简化为厚壁金属平板的情况,当然也包括薄壁平板这个特例。设图7中某块原始均匀温度为t0的板壳上存在直径2b范围内温度高达t1的局部变温。直径2b范围内的理论温度是图7中虚线所示均匀的t1,因此,在逐步缩小热应力计算区域的过程中,局部温度梯度模型涉及到尺寸大小问题。
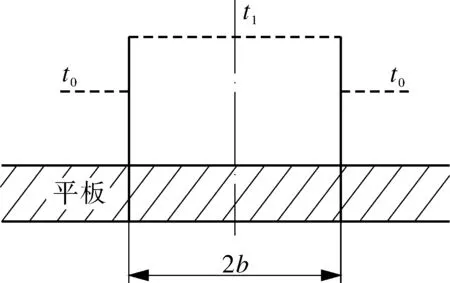
图7 热斑局部均匀温度模型
(1)传热过程的圆梯台热斑模型。
图8 热斑沿壁厚传热模型
在图8中厚度为δ的基板上侧加热一个半径为b的圆形表面小区时,热量在垂直传向基板的下表面时,也沿着水平方向传递,当热流穿透壁厚时,圆心处壁厚方向的温差最先变为零,模型开始趋于壁厚无温差的条件,其受热区可理想地构造为圆锥形(如图8(a)所示)。实际上,随着热流的继续传递,基板下表面的受热区逐渐扩大,形成一个半径为B的下表面热区,上下板面和板内的传热区构成一个梯形圆台,如图8(b)所示,半径B可视为壁厚无温差模型的板面几何尺寸。
文献[16]中构建了一个适用于平板两侧局部元件传热的等效热流模型,用来分析元件尺寸与传热效能的关系,具体在板翅式换热元件翅片尺寸优化中初步应用,设一块平板两侧分别有一体化连接的吸热翅片和放热翅片,当平板厚度小于吸热翅片的容积与翅片换热面积之比时,热流穿过平板的流程缩短,可以更快地从平板的一侧传递到另一侧,传热效率高,反之,则传热效率低;当平板厚度小于放热翅片的容积与翅片换热面积之比时,热流引过平板的流程缩短,可以更快地从平板的一侧引导到另一侧,传热效率高,反之,则传热效率低;而平板厚度太薄会削弱其结构强度和刚度,因此平板厚度存在合适的尺寸。这里引用其数学模型的原理,即:

(6)
根据上式对图8(b)梯形圆台建立关系式:
(7)
式中等号右侧分母的第1项是圆梯台的两个底面积,第2项是圆梯台的侧表面积。设介于理想模型和实际模型之间的热冲击模型,其状况是热量沿板厚传递效果不亚于沿板面方向传递效果,接近于使基板下表面的受热区也是一个半径为b的同等温度表面小区,如图8(c)所示,将B=b代入上式得:
(8)
整理得:b=±2δ。
取:
b=2δ
(9)
这是半径b与基板厚度δ的关系式,当对热斑表面半径尺寸检测之后可以应用上式对热斑整体范围进行基本的判断,也就是:被加热的小区半径≥2倍基板厚度δ时,基板壁厚肯定存在温差为零的小区,该小区沿板面方向的热应力就可理想地只考虑壁面温差来计算;被加热的小区半径<2倍基板厚度δ时,基板壁厚肯定存在温差,也就是板厚方向没有加热透彻,小区的热膨胀受到更多的限制,热应力更大一些,这是更符合实际的情况。
(2)传热过程的半(椭)球体热斑模型。
设传热过程热斑模型为图9所示的半球形,当热流穿透半球厚度,基于式(6)得:
(10)
整理得:
b=3δ
(11)
设传热过程热斑模型为图10所示的半椭球形,椭球体的3个半长轴为a,b,c,可设a=b,当热流穿透壁厚,有c=δ,基于式(6)取得式:
(12)
考虑到b (13) 因此,有: c>3δ (14) 当c=b,椭球形变成球形,由式(13)显然可推导得到式(11)。因此,当传热过程的热斑模型以半球体或者半椭球形代替圆梯台体,所得结果要求半径为b的值均大于式(9)的2δ,2δ是一个关于热斑模型穿透平板壁厚的最小值,可以把2δ作为模型尺寸的最基本要求。 图10 半椭球体热斑模型 一般地,热斑不但存在壁厚温差,还存在壁面方向的温差,后者的报导尚属空白。作为初步研究,首先简化模型,忽略热斑与其周边壳壁之间变形协调对其热膨胀应变的影响,并忽略热斑在平板中与其在壳壁中的差异,对热斑在平板中沿壁面方向的温差及其热应力进行分析讨论。 忽略壳结构的影响,视板壳为平板,参考图7,则该局部高温区与原来均匀温度区之间的热应力为: (15) 式中L-2b——下标,该物理量基于理想化2b斑区的物理量; E——材料高温度下的弹性模量,MPa; υ——材料泊松比; β——材料高温度下的线膨胀系数,mm/(mm·℃)。 由于局部高温区内的实际温度不均匀,如图11所示,设其中任意直径2a之外的温度为t2,且t1>t2>t0,可理解为在直径2b、温度为t2的斑中再存在一个直径2a、温度为t1的斑,其温度曲线如图11中的两级台阶水平实线所示。 图11 热斑局部温度梯度模型 两个叠加的热应力可以直接求和,这里不考虑相邻区域温差的交互影响所引起的热应力,所求热斑2b应力大小简单地按下式等于独立的2a区域的热应力与独立的(2b-2a)圆环区域的热应力之和,即: (16) 则斑中斑模型与单一斑内等温模型的热应力之差可由式(16)与式(15)相减得到,即: σ2b-σL-2b=0 (17) 结果是没有差别,这是因为式(16)的计算没有反映温度分布t1>t2>t0时热应力存在小区间相互作用的实际情况。 热斑温度分布的实际模型是单一斑内变温的,热应变属于弹性应变,所考察2b范围是很小的局部区域,其内部更小的各个小区域的热变形存在相互协调作用,小区域的热变形影响到整个热斑的变形,小区域的热应变影响到整个热斑的热应变,都应基于2b的尺度进行讨论,也就是说,所求实际温度的热应变的大小应等于独立的2a区域与独立的(2b-2a)圆环区域共同在基本区域2b范围内的热应变之和,其总的热应力为: (18) 式中S-2b——下标,该物理量是实际上2b斑区的物理量。 由式(18)与式(15)相减得: Δσ=σS-2b-σL-2b (19) 由式(18)与式(15)相加得: (20) 结合图11,在可以忽略的误差内,设虚斜线是一条直线,则有: 即: (21) (22) 将式(21),(22)代入式(19),整理得: (23) 将式(21),(22)代入式(20),整理得: (24) 关于式(23)的讨论如下。 (1)当a=b或b=a,即基本区域2b内不再分变温小区,而是温度均匀,即t2=t0,得Δσ=0,结果与式(17)相同,即图7理论温度模型是图11实际温度模型的特例,局部高温区内的实际温度一般都不是绝对均匀的。 (2)根据b>a,t1>t2,t2>t0,得Δσ<0,表明按图7理论温度模型计算的热应力总会大于按图11实际温度模型计算的热应力,结果与工程实际更加相符,一般地说,简单地按式(15)计算局部区域的热应力是偏保守和安全的。例如,当b=2a,相当于在更窄的热斑尺寸内出现同样的温差,温床梯度提高了,热应力也就提高了,代入式(19)得: (25) 上式的结果是式(15)所示理论模型结果的50%,间接说明热斑内计算热应力的模型尺寸对结果有影响,应力差值明显,在一个局部区域内再分小区时缩小尺寸使得热应力计算结果降低,在斑内分小区的计算方法偏危险,这是由于斑内温度分布较均匀的缘故,也进一步说明了只有掌握热斑模型及其尺寸,才能准确计算其引起的热应力。因此,进一步考察局部区域温度分布如图11中的斜虚线所示的普遍情况是有意义的。 如果常见局部温度模型可简化为图11虚斜线所示,满足工程要求而且较为简便的方法是在2a区内进一步划出直径为a的微区和径向宽度为0.5a的圆环形微区,根据式(25)的原理计算这些更小区域的热应力,在逐步缩小热应力计算区域的过程中,区域边界的温度是虚斜线上某点的温度,可按比例插值求取。 设图11中的虚斜线不是直线,而是较之稍复杂的曲线,如果把斑中变温分区和相应的温度分级得越细,则温度曲线的台阶数就越多,且越是逼近温度虚斜线。 设n表示热斑半径b与其局部区域内更小的分区尺寸半径a的关系,且n≥1,即b=na,当把该式代入式(23),且计算其极限,得: =0 (26) 上式推导的结果表明实际热应力的大小与式(15)的理论热应力相等,不存在应力差值。将式(23)和式(24)相加,整理得近似的实际热应力: (27) 将b=na代入式(27),且计算其极限,得: (28) 上式推导的结果表明实际热应力的大小与式(15)的理论热应力相等,也不存在应力差值。 综上所述,式(16)和式(28)从另两个角度趋于式(15)的结果,式(26)则从另一角度间接证明式(15)的结果是适用于工程的。无论斑区内温度分布如何复杂,式(15)是合理的。 针对式(26),(28)中与n有关的分子式和常数项,分别设应力差系数A和实际应力系数B: (29) (30) 并将此两个系数式绘制成曲线,如图12所示。当n=1,则A=0,B=1,与第3.3节(1)的讨论一致。 当n=2,则A=-0.5,B=0.5,有: (31) 图12 热应力系数分布曲线 上式推导的结果与第3.3节(2)的讨论一致,且与式(15)比较,2b区实际热应力的大小是理想化斑区热应力的一半,这是热应力差异最大的情况。 随着n的增大,图11中局部温度梯度模型的2a区越来越小,(2b-2a)区越来越大,该模型退变回图7的局部均匀温度模型,因此,图12所示的应力差系数A→0或实际应力系数B→1,两个系数都趋于稳定,且表明实际热应力的大小与理想模型热应力相等。总之,热斑应力可简便地按式(15)计算,而不会偏危险。 (1)区域中的圆环微区。 根据上述分析可以推断,如果分别在2a小区内进一步将其均匀温差(t1-t2)也分为2个微区,则微区内的实际热应力的大小可近似为: (32) 但是,不能据此推断在(2b-2a)小区内进一步把其均匀温差(t2-t0)也分为2个微区后,其微区内的实际热应力的大小也可类似按-0.5(t2-t0)βE计算,因为(2b-2a)小区是一个圆环小区,而不是一个圆形小区,其实际热应力的大小可由式(31)的2b区的热应力减去式(32)的2a小区的热应力而得: (33) 由此可见,圆环小区实际热应力属于压缩应力,其大小由两部分组成,-(t1-t2)βE/(1-υ)部分来自2a小区、向外热膨胀;-0.5(t2-t0)βE/(1-υ)部分来自圆环自身、向外热膨胀受到阻碍。 (2)独立的圆环小区。 有趣的是,如果式(33)中2a小区的温度与板壳上的原始温度t0相等,温度模型如图13中的虚线所示,则圆环小区的热应力从压缩应力转为拉伸应力: (34) 图13 圆环局部变温模型 应力性质的这种转变是由于中间的2a小区牵制住圆环小区,不让其向外膨胀的结果。 对热斑和冷斑的工程现象、理论概念及其热应力的认识尚属初步,总结文中分析可得如下结论。 (1)工程案例中常见壳壁局部区域沿壁面存在温度梯度的现象可称为热斑,实际上在斑的壁面几何范围内沿结构壁厚传热形成一个立体的小区域,因此热斑是立体的。热斑模型及其尺寸是准确计算其所引起的热应力的前提。 (2)平板局部区域沿壁面方向的温度梯度引起的实际温度的热应力大小等于该区内相邻并独立的各个小区的热应力之和,但是各个独立小区的热应力存在相互作用。通过在热斑内逐步缩小区域范围可以直接逼近计算微小区的热应力,但是其结果会低估热应力水平,使判断偏危险。无论斑区内温度分布如何复杂,热斑应力简便地按式(15)计算都是保守的。 (3)一个局部区域可以划分为中间微小区和绕在该中间微小区周边的圆环形微区,周边圆环形微区的热应力可间接通过这两个微区组成的局部区域的热应力、减去中间微小区的热应力得到。 (4)计算热斑应力时,平板局部区域存在合理评估局部温差范围的几何尺寸,也就是壁厚无温差模型的区域尺寸。被加热的局部小区半径≥2倍基板厚度δ时,才存在壁厚温差为零的小区,否则,该小区沿板面方向的热应力就要加上壁厚温差引起的热应力,总的热应力要比式(24)的计算值更大。文中推导的壁面方向热斑应力计算公式、热斑几何尺寸计算式及热斑最高许可温度计算式简明易用。 图4初步反映了JB 4732—1995(2005年确认)中规定的回转壳经线方向的测定间距与平板表面温差的测定间距的因素关系,不是两个测定间距的实际关系。但是,基于平板模型推导的结论应用到壳体模型时存在偏差,其中包含的物理本质关系有待进一步研究。因此,文中基于平板中的热斑模型及其假设条件推导的热应力计算式,应用于平板或者壳壁的热应力计算时,其有效性有待验证。 式(6)的基本原理由笔者在前几年研究的另一专题中提出,详见文献[16],这里引用作为热斑基本模型及尺寸的计算公式,其合理性是否值得怀疑,欢迎讨论。 图12中当n=2时的系数曲线从下降转向上升,这是一个拐点,而且n值不一定总是以整数来表示热斑半径b与其局部区域内更小的分区尺寸半径a的关系,关于n的意义、取值以及拐点的影响因素,显然值得另文进一步研究。 在本文研究的基础上,如同文献[1-2]那样,也可以推导得壳壁局部区域免于屈服变形的最高许可温差或温度,也值得另文研究。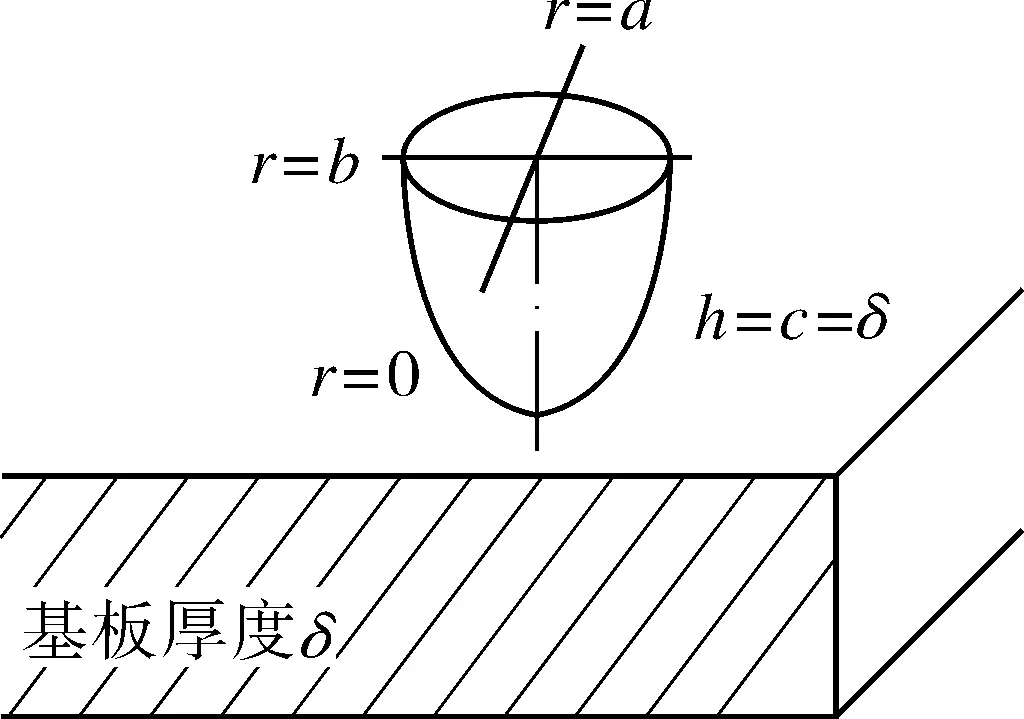
3 热斑温度分布及其热应力
3.1 单一斑内等温模型及其热应力
3.2 斑中斑模型及其热应力
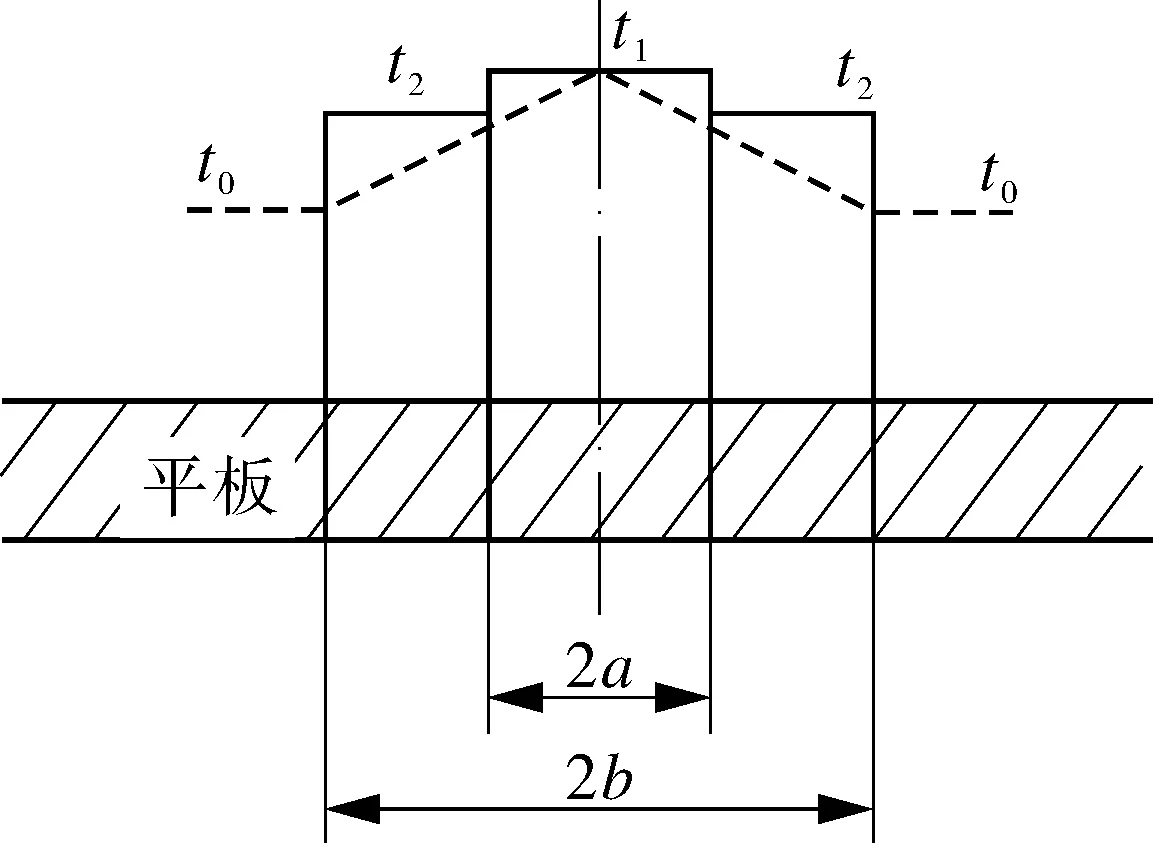
3.3 实际模型的简化及其热应力
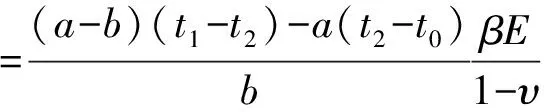
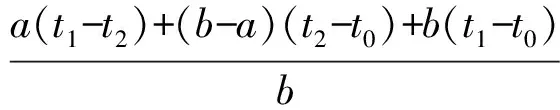
3.4 单一斑内复杂变温模型及其热应力



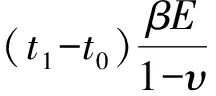
4 热应力系数

5 圆环小斑区的热应力

6 结论
7 值得进一步研究的问题

