空间微重力组合体及其控制

于绍华

中国科学院 国家空间科学中心,北京 100080

100多年前，俄国宇航先驱齐奥尔科夫斯基指出，从太空船(母星)放出一个用长线系留的平衡质量物体(绳系子星)，可产生人工微重力ΔG≈3ω2Dm。其中ω为母星的轨道角速度;D为子星放出距离；m为子星的质量。这是齐氏对绳系卫星的预言[1]。

母星、子星和连接它们的特制长长的柔软细线构成了绳系卫星系统(简称TSS)。微重力、系统运动产生的惯性力和控制作用力等沿系绳传送到系统的其他部位，以支撑和改变(控制)TSS的内外构形，扩充科学实验平台，探索人类进入太空生存的微重力环境和重力科学等[1-3]。

20世纪后期航天界掀起TSS热，发表了不少文章和研究计划，做了数十次太空验证飞行，但并未取得突破性进展，热潮也慢慢退去。这主要有两个原因：一是那条超长、纤细、轻质又高强度的系绳和附件，给材料科学和制造工艺带来极大的挑战；二是如此大跨度和多自由度的柔性系统的动力学空前复杂，涉及许多不稳定运动，尚未研发出有效的控制办法。

迄今为止，验证飞行用的绳系子星的质量不超过500 kg，母星的轨道高度不到400 km，系绳的设计长度仅为几十千米。这些小号的绳系卫星系统，设备简单，功能有限；必须开发出更大、更强的产品以打破TSS的瓶颈，开辟新天地。

本文设想的空间微重力组合体(简称为SMC)是增强版的TSS，它由较大的空间主站、系绳收放操作系统及绳系实验吊舱(相当于TSS中的母星、系绳和子星)所组成。其中的绳系吊舱犹如一艘小太空船，装有多种必要设备，除保障科学实验，还要介入SMC整体运作。SMC是异常复杂的大型航天工程系统，不只要求有强大的硬件依托，还要有可靠的软件来控制SMC系统在轨运行。

文中研究了TSS家族(包括SMC)的控制策略，重在阐述距离速率控制算法，推进TSS的发展。

1 SMC的可行性

1.1 硬件设备

主站和吊舱(可由天地往返输送飞船改装过来)都具有测轨调轨、测姿调姿和测距定位功能，其材质、工艺和设计制造乃至组装联调都和通用航天器相差不多，技术条件比较成熟，可行性很大。系绳的收放和伸缩操作系统是连结站、舱和施加调控的关键环节，是很有挑战性的创新研究。

1.2 系统组建和运作

SMC的最后成形不是一蹴而就的，而是逐项逐次完成。可以设想的单吊舱方案是：首先将主站和系绳操作系统打包一起送上近圆轨道；然后由地面发射吊舱使其入轨并与主站交会对接(简称RVD)；待系绳锁紧后，以绳系卫星工作模式将吊舱放逐到设定空域并启动科学实验；实验结束后，将绳系吊舱收回到主站中，准备重复使用。此处的绳系吊舱把TSS和RVD两项功能集于一身成为双料吊舱，而SMC也可由单吊舱扩充成多吊舱系统。

1.3 工程控制

SMC的主站和双料吊舱都兼有TSS(涵盖系绳展开、留位和回收3种运动模式)和RVD两大功能和控制技术。此外，吊舱还具有相应的姿态控制技能，为舱上科学实验提供所需并在必要时协助完成对SMC运动控制。

20世纪70年代起，对地应用卫星的姿态控制理论和工程实践技术有了空前大发展，已纳入规范化的轮控技术范畴[4-6]。不过，SMC吊舱的姿态还受到系绳拉力的制约， 由此增加了新的研究内容。

SMC的另两大项控制是RVD和TSS。在RVD方面，苏美在20世纪60年代就已掌握和多次成功实现了两个单体航天器在轨交会对接[7]。 苏联采用的是平行/比例视线导引法，构思简明，安全可靠，但其动力学特色不足且交会轨迹不易预判；美国则推崇C-W方程法，颇有新意，然而其线性化系统误差和开环脉冲程序控制误差不可低估。 SMC较单体航天器复杂很多，苏美的经典方法已不适用，承担不了更高端的SMC控制，需要开发新的RVD控制技术。

在TSS方面， 一个长久困扰航天界的问题是绳系卫星的留位和回收运动是不稳定的。 如不解决稳定控制，就无从谈起TSS及SMC的应用。为此，有人提出了不同方案，其中有一方案被称作“距离速率控制算法”(Range Rate Control Algorithm，RRCA)， 把同属于航天器相对运动的TSS和RVD统一融合起来，用严整划一、简捷实用的方式实现它们的运动稳定，可望打通TSS和SMC成功之路。

2 TSS控制中的RRCA算法

TSS控制的三要素是简而明的动力学模型、选择输入(控制)变量和制定控制算法。

在空间站(母星)固联轨道坐标系中，吊舱(子星)的轨道面内运动，即距离向量D的长度D和方位(相)角φ两个分量运动的简化模型是[7-8]:

(绳张力T>0)

(1)

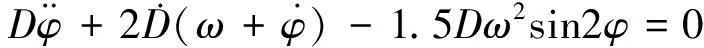
(2)

1)著名的RUPP提出了以系绳拉力为主导的控制算法[9]：

式中：Df为驱动距离。

试图在式(1)中激发出谐振，通过藕合效应控制式(2)中φ角运动，但没成功，因为：

——很难达成强藕合；

——柔绳对力的传导机制非常复杂。

此后，有关文章不断列出各种控制方案，它们的理论意义、实用价值乃至是否对症尚待核查。

2.1 RRCA的构建(基础型RRCA)

在TSS的理论研究和应用实践中，存在某些具有特殊价值的特定运动形态(例如平衡状态)，认识和发现这种运动的性质和规律对解决TSS的稳定控制会有启示作用。

将方程(2)改写成：

由此，可解出组合变量与φ角运动的关系，继而对此变量给予创造性赋值，此过程结果可示为：

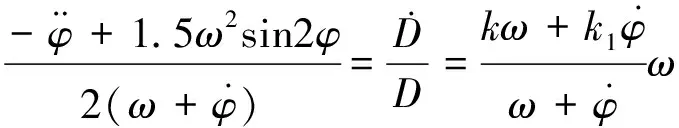
(3)

此式把三组动态函数(对应控制三要素)关联起来，是颇具控制潜能的三联等式，是指导创建RRCA的路引。

(4)

式中：k∈(-0.75,0.75)，k1>0。

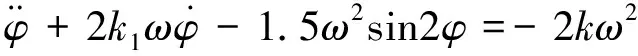
(5)

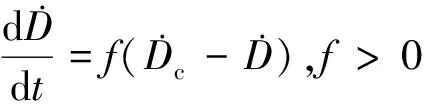
(6)

此时式(2)给出的TSS相角φ的运动是稳定的，在短暂过渡之后进入定常稳态(包括极限环)。 由式(4)和式(6)构成的“距离速率控制算法”叫做基础型RRCA[10-11]。RRCA包含TSS的三种运动模式的距离D的程控指令部分也有φ角运动的速率稳定控制指令部分，是一种统合稳定控制。

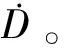
把式(6)代入到式(1)中，将得到由RRCA主导的、不同于RUPP理念的系绳拉力复合控制算法:

Dω2(3sin2φ-1)]

2.2 扩展型RRCA

1)母星(主站)沿椭圆轨道运转时取

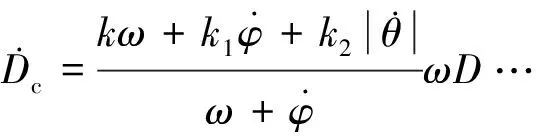
3)2006年，有学者提出了“改进的绳系卫星系统距离速率控制律”[12]：

1) 催生了基础型RRCA，解决了简化的TSS模型的稳定控制；

2) 在非简化的TSS动力学模型控制时， 扩展型RRCA将起到主干核心的作用；

2.3 计算机模拟[11]

图1是在RRCA制导下的美国航天飞机TSS-1计划中的子星向后上方放出、留位和回收时在轨道坐标系里的全程运动轨迹(包括进出极限点)； 图2是母星轨道为大椭圆时，子星向前下方放出、留位和回收时全程运动轨迹(包括进出极限环)。在RRCA控制下，TSS的全程运动都是稳定的。

图1 TSS-1子星轨迹Fig.1 Subsatellite′s trajectory in TSS-1

图2 母星轨道为大椭圆时的子星轨迹Fig.2 Subsatellite′trajectory on ellipse orbit

3 RRCA在RVD控制中的应用

航天器在轨共面交会运动方程为[14]：

(7)

(8)

方程式(7)(8)与式(1)(2)在主体上是一致的，因此，RRCA对它们都是适用的。再者，RVD已有多年的基础研究和丰富的实践经验，其系统功能强大(可以安装1个或3个轴向推力器：as、aφ、aθ)，而其动力学要比TSS简单得多。与TSS不同，RVD不存在系统性的不稳定运动和系绳所具有的复杂的非线性偏微分方程系统的动力学模型[13]。这也是为什么RVD技术早已解决，而TSS尚待攻克的原因。可以想象并且计算机模拟结果也证明了： 在RRCA控制下RVD的效果非常完美。

3.1 单轴推力器系统

采用单一的纵轴向推力as并定义以下约束条件：

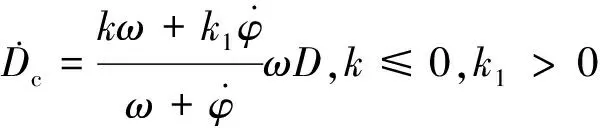
(9)

推力器输出的控制逻辑是：

(10)

由方程(7)～(10)构成的单推力基础型RRCA闭环控制算法，足以完成一般条件下的交会任务。

3.2 三轴组合推力系统

选用三轴推力器方案，可以实現任意指定方位上的交会，即360°全方位交会[15-16]； 还远不至此，RRCA算法可以把RVD全过程中的追踪靠近、 驻泊、 绕飞和悬停等多种分段性任务集于一身一次完成，这是很大的优点。

航天器三维空间的RVD闭环控制系统方程为:

Dω2(3cos2θsin2φ-1)=as

(11)

1.5Dω2sin2φ=aφ/cosθ

(12)

1.5Dω2sin2θsin2φ=aθ

(13)

(14)

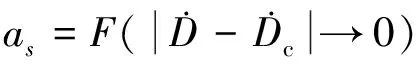
(15)

aφ=(asin2φ+bcos2φ)ω2D

(16)

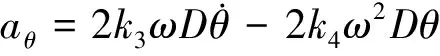
(17)

a=-1.5+2ksin2φd-0.5qcos2φd

(18)

b=2kcos2φd+0.5qsin2φd

(19)

式中：φd为设定的交会方位角；q>0；k,k1,k2，等参数均可选。

3.3 计算机模拟

图3是吊舱等机动船(M)与空间站等目标船(T)在RRCA控制下的交会追踪接近段轨迹，图4是绕飞、 悬停和驻泊停留段的运动轨迹[7]。 采用扩展型RRCA与RVD相结合，也可以产生多种控制结果[17-18]。

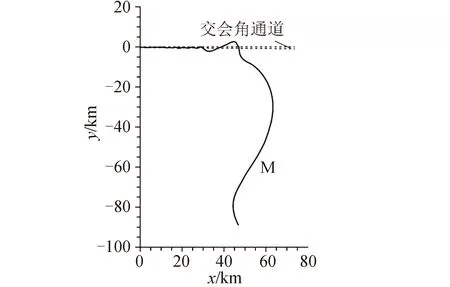
图3 接近段轨迹Fig.3 Rendezvous trajectory

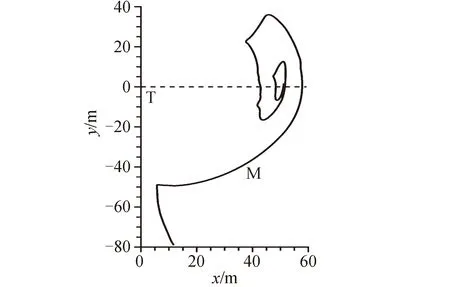
图4 绕飞、悬停、驻泊段Fig.4 Round flight trajectory

RRCA是一套理论、一组方法和一种架构，即能控制TSS也能操作RVD。该算法立论深邃、推理严谨、结构明快且富于变化,易于实现，为理论分析和数字模拟所验证。

4 结束语

20世纪70年代诞生了绳系卫星的现代概念，科学家们提出了十数计的空间应用设想，进行了多次验证飞行，却鲜有满意收获[19]。除机械故障外，对该系统理论和控制方法认识不足也是主要原因(例如美国TSS-1飞行试验采用的还是开环的程序控制[3])。

时至今日，TSS的简化模型及有分布质量和弹性变形的系绳系统模型仍是当今TSS控制的难点，距离速率控制算法和空间微重力组合体是其研究重点。空间微重力组合体的硬件核心是双料绳系吊舱，它兼顾了绳系卫星和飞船交会两项功能；组合体的软件核心是距离速率控制算法，它把绳系卫星和飞船交会控制整合统一起来。这样的硬软结合，形成了组合体的总体框架和组合控制原则。若将它们落实到未来的验证飞行中，相信会取得所期盼的结果，为绳系卫星和飞船交会开辟新径；为空间组合体在更复杂的作业区, 如高轨道区(对系绳更安全有利)和静止轨道区(如观测外太空-绳系吊舱环球布网)，为多吊舱串连系统创造条件并展现广阔前景。