霍尔推力器羽流对S波段电磁波的衰减研究
232323*
1. 电子科技大学 信息地学研究中心,成都 611731 2. 上海空间推进研究所,上海 201112 3. 上海空间发动机工程技术研究中心,上海 201112
霍尔电推力器羽流属于低温等离子体媒质,对于穿过羽流的电磁波会产生信号衰减的影响。其中,以S波段受霍尔推力器羽流影响最为显著。这是因为,对于霍尔推力器羽流参数,整体电子数密度在1013~1015m-3量级,电子温度在1.0 eV量级,这使得C波段和Ku波段的电波在羽流中具有非常显著的高通特性,相比之下,S波段是电波最易受影响区间。因此,针对S波段电磁波受霍尔推力器羽流影响的研究具有重要意义。
截至目前为止,关于霍尔推力器羽流对于电磁波的影响研究鲜有报道,但与之相关的等离子体对电磁波的影响研究在20世纪90年代已有报道。研究人员最先关注的是“等离子体隐身”[1-3]技术,该技术主要采用飞行器制造的等离子体氛围来吸收电波或折射电波以实现被探测飞行器对雷达扫描的规避。其次,“黑障”问题[4-6]的出现再一次让研究人员聚焦大气等离子体环境及天线表面鞘层等离子体对电磁波的影响问题。根据大量研究,等离子体对电磁波的影响主要有吸收、折射、反射、多普勒效应以及法拉第旋转等[7]机制,但对于信号衰减问题来说,吸收和反射是主要影响过程;当离子数密度超过105倍电子数密度时,离子才会对电磁波产生较显著影响,因而,在低温平衡态等离子体中,对电磁波的衰减作用主要依靠电子[8];等离子体频率、电子-中性粒子碰撞频率是对电磁波衰减的主要物理参数,在电磁波频率低于等离子体频率时,电磁波在等离子体边界易发生反射,故等离子体频率可视为电磁波高通特性的截止频率[9],而当电磁波频率高于等离子体频率时,电磁波在等离子体内可进行有衰减传播,此时,衰减主要由吸收作用导致(电磁波能量被电子吸收,电子再将这部分能量通过与中性粒子的碰撞来提升中性粒子的热运动能量);等离子体分布的不均匀性会导致电磁波的衰减效应更加明显[10]。综上,现阶段研究人员更加关注非均匀等离子体对电磁波的衰减情况[11-13]。
霍尔推力器羽流属于非均匀等离子体,其参数分布具有很强的特殊性,相关电波衰减规律难以通过现有研究结论来预估。同时,羽流对通讯信号的影响直接关系到整星布局设计,是急需研究的重点问题。因此,本文将针对天线在不同位置时,S波段电磁波受霍尔推力器羽流衰减的信噪比衰减规律进行深入研究。
在研究方法方面,由于金属真空舱对电波的屏蔽作用较强,而透波舱又很难覆盖较大的羽流区域,使得试验方法无法实现羽流远场的电波衰减测量,因此本文将主要采用数值方法来进行研究。在算法方面,几何光学法、解析法以及时域有限差分法(FDTD)[14-16]是近年来比较常见的方法。考虑到本文计算工况较多、计算速度为优先的原则,本文将采用几何光学算法来实现电磁波在等离子体内部的传输过程模拟,并且以空间透射波法对固定天线位置的电磁波在羽流中的信噪比衰减进行测量,以试验结果与相同工况计算结果进行对比,验证几何光学算法在霍尔推力器羽流环境中的计算精度。最后,针对霍尔推力器0~5 m范围的羽流场对S波段电磁波的衰减信噪比进行数值计算,并分析相关规律与机理。
1 算法
首先,电磁波在等离子体中的传输过程是一个关于电磁波和等离子体之间相互影响的耦合过程:电磁波会影响等离子体各项粒子分布参数,且等离子体媒质会影响电磁波传输功率。那么,本文采用几何光学算法需要基于一个假设:仅考虑等离子体对电磁波的影响,而忽略电磁波对等离子体输运过程的影响。
1.1 等离子体媒质特性
霍尔推力器羽流参数的计算是为电磁波传输计算提供媒质特性的输入条件,因此,这部分计算与电磁波计算是独立的两个过程。现阶段,关于霍尔推力器羽流计算的研究较为成熟,但就本文所关注的羽流参数(电子数密度、电子动能和中性粒子数密度)而言,羽流计算当以电子为主,为此,本文采用文献[17]中提到的全粒子模拟方法,其中,中性粒子分布采用半经验求解法,离子和电子的输运过程详见文献[17]。需要说明的是,在羽流输运过程计算的输入条件中,与文献[17]一致,Xe的正离子成分比例为80%的Xe+和20%的Xe2+。
这里,本文主要介绍对计算得到的等离子体参数分布场的后处理方法,所谓“后处理”是指利用羽流参数(电子数密度Ne、电子动能Ek,e及中性粒子数密度Nn)推导出媒质特性参数(等离子体角频率ω0和电子-中性粒子碰撞频率ve-n)的过程。
等离子体角频率求解如下:
(1)
式中:e为元电荷,取1.6×10-19C;me为电子质量;ε0为真空介电常数,取8.85×10-12F/m。
电子-中性粒子碰撞频率求解如下:
νe-n=Nnveσtotal
(2)
式中:σtotal为电子与中性粒子的总碰撞截面,可由弹性、激发及电离碰撞截面之和来进行求解。上述3种电子与Xe原子的碰撞截面公式见表1。
本文所采用的计算输入条件见图1。图1(a)(b)(c)为羽流等离子体分布参数,图1(d)(e)为羽流媒质特性参数。文中试验与计算所采用的霍尔推力器信息如下:推力器代号HET-80,放电电压300 V,放电电流4.5 A,阳极气体流率53 mL/min,阴极气体流率3 mL/min,励磁电流4.5 A,推力79.6 mN。
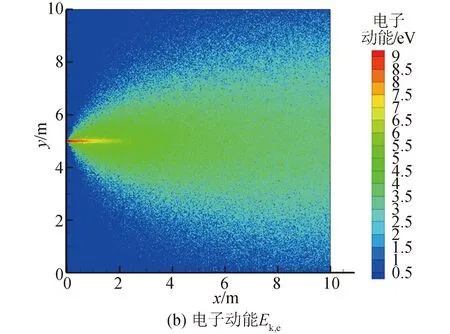


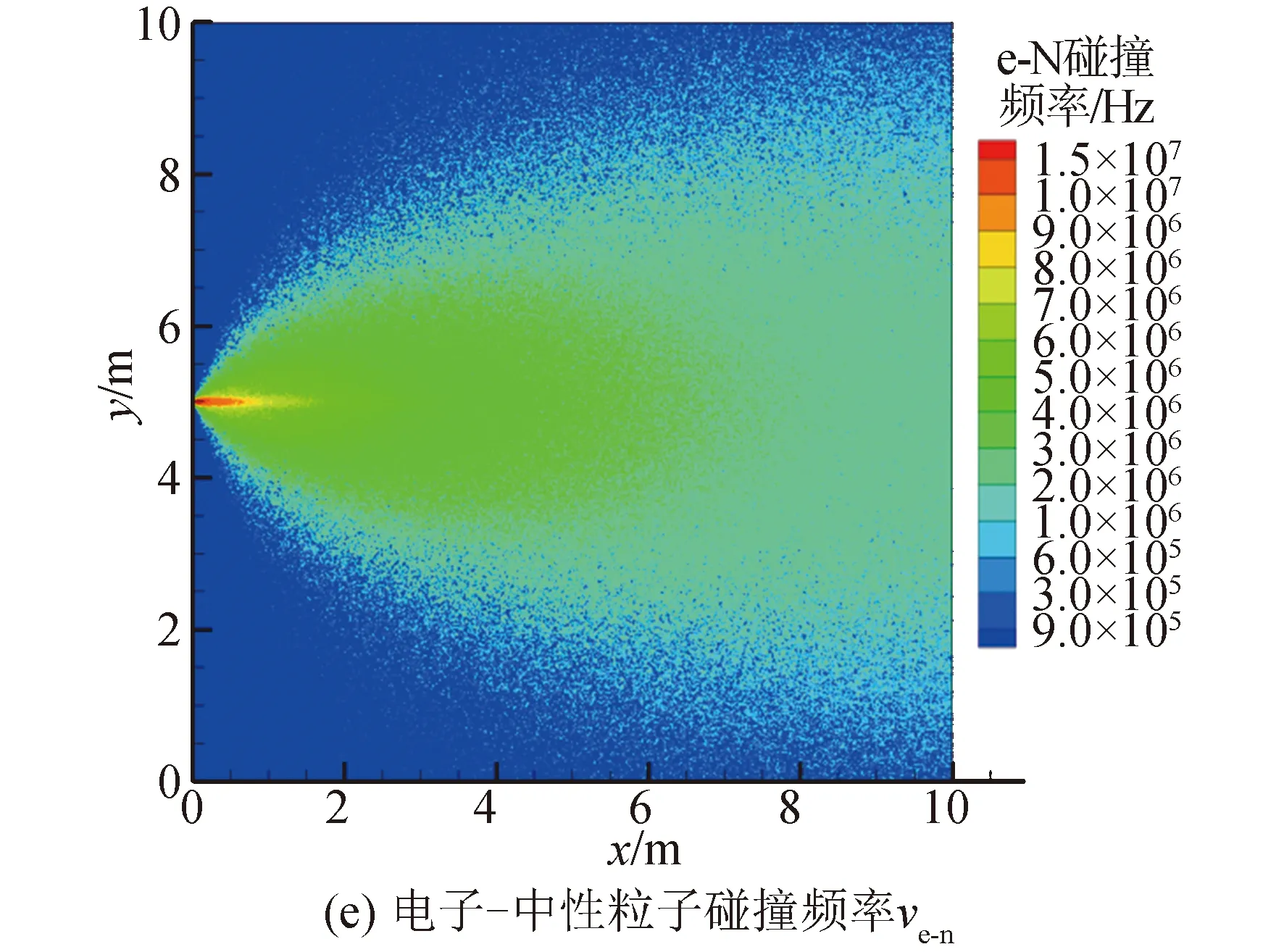
图1 HET-80霍尔推力器羽流的等离子体参数分布及媒质特性Fig.1 Plasma parameters and medium characteristics of HET-80 Hall thruster plume
1.2 电磁波衰减
在羽流媒质特性参数获得求解后,电磁波在等离子体中的衰减过程可以进一步被描述。首先,当一束电磁波穿越羽流媒质时,其“光路”将依次穿过若干计算网格,如图2所示。在光路上会分布等距计算节点,取节点间距l=0.5 mm,以第1.1小节计算得到的ω0和ve-n分布来对光路节点进行插值(采用面积权重法),以求解电磁波在光路节点间传输时的衰减情况。电磁波在经过羽流边界和羽流内部每个光路节点时的功率衰减算法如下。

图2 电磁波传输的几何光路法Fig.2 The geometric light-path method for the electromagnetic wave propagation
假设一束功率为Pi的电磁波进入某个计算节点,如果该节点在边界处,则反射功率为Pr,若节点在羽流内部,这一项取0,接着,电磁波在该节点到下个节点间被等离子体吸收功率为Pa,透射功率为Pt,那么,有如下关系:
Pi=Pr+Pa+Pt
(3)
式中:Pr和Pa是影响信噪比衰减的参数。
在边界处的反射功率Pr为[18]:

(4)

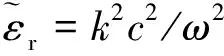
(5)
穿过每个微元路径(长度为l)的透射功率Pt为:
Pt=(Pi-Pr)exp (-2kel)
(6)
式中:ke为由电子引起的电磁波衰减系数。将式(4)和式(6)带入式(3),可以反推计算Pa。
衰减系数ke的求解方法如下:

(7)
这里,式(7)中的ω0和ve-n来自图2中插值结果。
电磁波信噪比为:
SNR=10lg(Ps/Pn)
(8)
式中:Ps为电磁波有效信号的功率;Pn为背景噪声功率。这里,认为Pn不受羽流影响,Ps会受衰减影响,若电磁波在整个光路上的衰减功率为ΔP,那么信噪比的衰减值为:
ΔSNR=10lg[(Ps-ΔP)/Ps]
(9)
1.3 算法的验证

图3 验证试验布局Fig.3 Schematic diagram of the verification test layout
数值模型的验证试验采用空间透射波法,如图3所示,该试验于真空舱(舱壁材质为不锈钢)与透波舱(舱壁材质为玻璃钢,纤维增强树脂基复合材料)连接形成的真空环境中进行,在透波舱外布置屏蔽暗室,保证测量信息不受其它电磁波干扰,透波舱对1.5~3.5 GHz频率电磁波的透过率较高,单独测量透波舱对电磁波的衰减在0.75~0.80 dB。以机械泵、分子泵和扩散泵组成的泵组来完成真空抽气,在推力器正常工作时,真空度可保持在4.5×10-3Pa。发射天线的电磁波传播方向与推力器轴线恰好垂直,天线距离推力器出口1 m。发射天线在S波段的频率调整步长为0.01 GHz,即整个S波段共有186个工况点。
试验与计算结果见图4,其中,试验结果增加了透波舱对电磁波的衰减值。计算结果的最大相对误差在26.1%,平均相对误差在7.3%。在总体变化趋势上,计算与试验结果基本一致。值得注意的是,在电磁波工作频率较低时,信噪比衰减结果的误差较大,这里考虑几何光路法本身所带来的误差:实际电磁波传输路径应是一个发散角较小的圆锥区域,而非一根直线,这令电磁波沿程穿过的等离子体区域放大,令计算值与试验值出现误差,这种误差在频率较高时并不明显,但在频率较低时会得到放大。此外,本文重点考虑的是“电子-中性粒子”的碰撞效应,而忽略了其他种类的碰撞效应,这种假设也会增加试验与计算结果的误差。

图4 试验与计算结果对比Fig.4 Comparison of the test and calculation results
试验结果具有较大的波动,这与屏蔽暗室内的仪器电路所产生的电磁波、以及推力器放电振荡有一定关系。此外,试验结果的衰减程度比计算结果小,这里推断是透波舱对推力器羽流有一
定的束缚作用,使得电磁波的穿越路径长度比计算设定的长度短。
2 计算结果与分析
在验证算法的计算精度后,本节将针对卫星上天线与推力器可能存在的典型工况进行计算。所有计算工况点的分布见图5,天线位置共选取12个坐标点,天线朝向共7个方向角,共84个计算工况。S波段电磁波频率的选取步长为0.01 GHz。
关于84个天线布置工况的信噪比衰减计算结果见图6。

图5 计算工况介绍Fig.5 Introduction of all computational cases
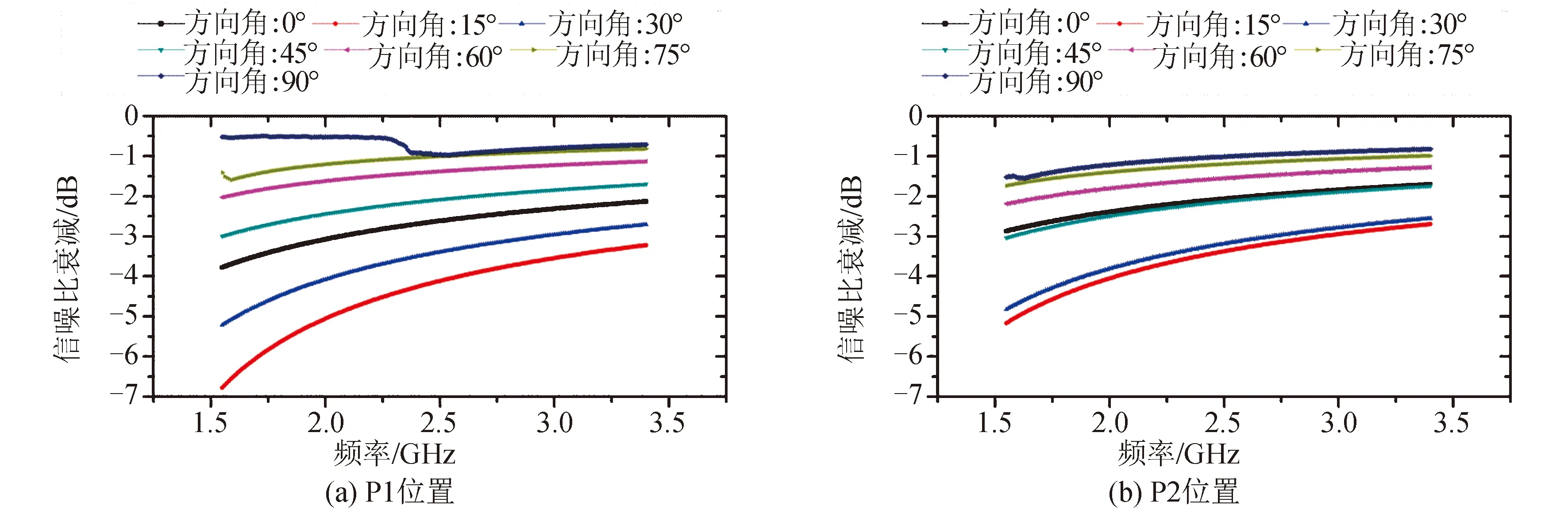




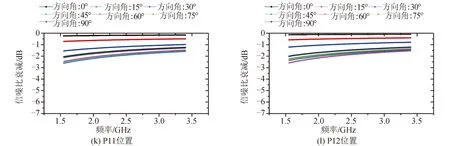
图6 各工况下信噪比衰减值随电磁波频率的变化规律Fig.6 Changing rules of the attenuation SNR vs wave frequency at different cases
根据计算结果,随着天线位置距离推力器增长,信噪比的衰减程度在整体上基本呈降低趋势(个别工况如P11和P12有微小差异) ;然而,随着天线方向角的变化,信噪比衰减程度的变化并无明显规律,例如,在P1和P2位置,15°是衰减最大角,但在P3~P6位置,30°是衰减最大角,而在P7~P11位置,45°又成为衰减最大角,P12位置处,60°为衰减最大角,以及在图6(k)(l)中,45°与60°工况对应的衰减趋势不同等。而且,其余角度的衰减程度排名也会随位置变化而变化,以上均说明信噪比衰减程度与天线方向角的相关性不显著。在全工况中,信噪比衰减最大工况为P1位置15°,衰减第2工况为P1位置30°,衰减第三工况为P2位置15°。值得注意的是,这些衰减较大工况的几何光路所在区域的参数ve-n并不是最恶劣,这与现有理论研究有一定差异,考虑这与羽流分布的不均匀性和特殊性有较大的关系。
此外,由于P1位置90°工况下羽流内的光路过短,导致计算结果出现了低频下的衰减降低,以及衰减的峰值点,类似结果也出现在了P1位置75°和P2位置90°的工况。但是,对于其他工况而言,羽流中的光路较长,衰减的峰值点就会降低到更低的频率区间,已经小于这些工况的频率横坐标的最小值(1.55 GHz),故并未在其他工况曲线中出现衰减的峰值点。
进一步地,针对图6计算结果进行更深入的分析。根据数值模型,电磁波在等离子体中衰减与电磁波的反射和吸收作用有关。图7给出反射最恶劣的P1和P2位置、单独由反射作用所引起的信噪比衰减结果,计算结果说明,反射作用产生的信噪比衰减在-0.05~0 dB之间,相比吸收作用而言,反射作用的影响不占主导。


图7 由反射作用引起的信噪比衰减Fig.7 The attenuationSNR caused by the reflection action
因此,霍尔推力器羽流对电磁波的衰减主要由吸收作用导致。由此,图8给出各几何光路上各计算节点的吸收率分布(吸收率定义为该节点所吸收的功率与达到该节点的总功率之比,Pa/Pi)。根据计算结果,距离推力器出口越近的区域吸收率越大,但整个光路的信号衰减不仅仅取决于吸收率大小,还与具有一定吸收率(不妨取1.0×10-4,图8中对应标尺颜色为青色)的光路长度有关,例如,P1位置90°工况是经过推力器出口最近位置的工况,该光路穿过了吸收率最大的区域(该区域的电子-中性粒子碰撞频率ve-n最大),但光路青色区以上的长度较小,所以在P1位置,90°却成了衰减最小方向角。但随着天线位置的远离,情况有所改变,例如,在P5位置,90°的衰减程度为倒数第2,P7位置,90°的衰减程度为倒数第3,P12位置,90°的衰减程度为倒数第4。故羽流对电磁波的吸收作用主要与两个因素有关:第一,几何光路所穿过区域的吸收率大小;第二,几何光路保持一定吸收率的有效长度。与已报道理论不同的是,霍尔推力器羽流虽然属于非均匀等离子体媒质,但羽流中的光路有效长度会随着位置、方向角不同而发生无规律性变化,而一般的非均匀等离子体媒质的吸收作用只受第一个因素影响。由此,导致了图6计算结果与现存报道规律的不同。

图8 各几何光路上的吸收率分布Fig.8 The distribution of the absorptivity on each geometric light-path
3 结束语
本文针对霍尔推力器羽流对S波段电磁波的信噪比衰减影响进行研究,主要结论如下:
1)天线与推力器的距离增大对信噪比的衰减有降低作用,但天线方向角的变化对信噪比衰减无明显规律,衰减最大工况区域出现在天线位置0.3~0.6 m、方向角15°~30°的区域,衰减值在-7~-4 dB之间;
2)羽流对电磁波的信号衰减主要由吸收作用导致,与电磁波几何光路所在区域的吸收率和具有一定吸收率的有效光路长度有关,这导致霍尔推力器羽流对电磁波的衰减规律与其他非均匀等离子体媒质有较大差异。

