高考数学思想应用于三角函数解题教学研究
陈培培
(江苏省如东县掘港高级中学 226400)
一、高考数学背景下三角函数教学概述
根据高考数学命题大纲要求,高考数学命题不仅要考查学生对数学基本概念和知识的掌握情况,还要考查学生对数学思想方法的灵活应用和数学思维的厚度.通过对近些年高考数学试题的统计分析发现,关于三角函数的考试题型正在不断发生变化,其中涉及到的选择题、填空题正在逐渐减少,解答题的数量逐渐增加,考查知识的重点放在正余弦定理、倍角公式、辅角公式、图象平移、三角形面积公式等.对数学思想的考查主要是化归思想、分类讨论思想和函数与方程思想.需要注意的是,要在这些问题的讲解过程中渗透数学思想,提升学生的数学思维.
二、高考数学背景下数学思想应用于三角函数解题教学实践
为了更加直观地阐述高考数学背景下数学思想应用与三角函数解题的应用,下面通过具体的数学教学设计来进行分析,设计主要围绕教学目标和教学过程展开.
1.教学目标
通过该部分知识的教学,学生能够了解高考数学三角函数部分的高频考点,掌握数形结合思想、化归思想、函数与方程思想在三角函数具体解题中的应用,知道高考数学三角函数部分主要考查的数学思想方法.同时,通过高考真题的讲解与分析,全面认识高考数学问题,提高学生对三角函数部分的学习信心.
2.教学过程关键环节
(1)化归思想在三角函数解题中的应用
例1在△ABC中,a、b、c分别是角A、B、C对应的边,其中a2-c2=2b,且sinAcosC=3cosAsinC,求b的值.


(2)分类讨论思想在三角函数解题中的应用

①求出φ的数值.
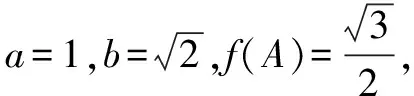
分析该题主要是考查学生根据正弦定理求三角形的边和角,计算出三角函数中两角和差的正弦函数公式.




(3)函数与方程思想在三角函数解题中的应用


②已知sinC+sin(B-A)=2sin2A,求出△ABC的面积.
分析本题可以利用函数与方程思想,通过正余弦定理、三角形的面积公式联立方程组进行求解.

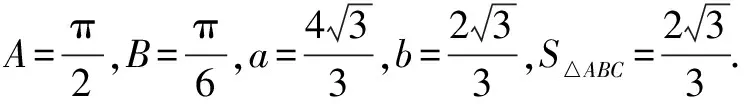
化归思想、分类讨论思想和函数与方程思想是三角函数解题过程中常用的数学思想,也是高考数学三角函数部分考查的热点.在三角函数部分教学中,教师可以选择一些高考真题,有意识地向学生渗透数学思想,帮助学生分析这些高考数学问题,了解高考数学三角函数部分问题的特点,提高学生利用数学思想解决三角函数问题的能力,为学生参加高考奠定坚实基础.

