高中数学课堂渗透核心素养的几种探索
文/台山市台师高级中学
数学核心素养培养的缺失,会让学生离数学的内核越来越远。这是高中数学课堂面临的一个非常突出的问题。所以,在现代的高中数学授课中,我们要在课堂上创新地渗透核心素养,采用有效的教学方法,激发学生兴趣,让学生不但会学数学,更会应用数学。
一、创设问题情境,激发学生学习兴趣
课堂教学成功与否,很大因素在于能否调动学生学习的积极性,激发学生的兴趣。所以创设一个合理而有趣的情境是很重要的。好的问题情境往往能够激发学生浓厚的学习探究意识,迎难而上,激发自身最大学习潜能。
例如,在《几何概型》的教学中创设以下四个情境:
情境一“飞行棋游戏”是我们都熟悉的一种游戏,规则为参与游戏者轮到掷骰子的时候,必须掷到6的时候飞机才能“起飞”,试问能“起飞”的概率有多大?
情境二记函数f(x)的定义域I={x∈N|-2≤x≤3},在区间[-5,6]上随机取出一个整数x,求x∈I的概率。
情境三记函数f(x)的定义域I={x∈R|-2≤x≤3},在区间[-5,6]上随机取出一个数x,求x∈I的概率。
情境四已知球O内切于棱长为4的正方体,现在正方体内任取一点,求这点在球内的概率。
情境一目的是引起学生学习的兴趣。从情境一到情境二,符合由具体到抽象的思维习惯,通过情境二,再次复习古典概型“有限性”和“等可能性”的特点。由情境二到情境三,学生将会产生认知上的冲突,情境三概率求法能不能跟情境二一样?为什么?两者有何区别?由此,类比得出几何概型的特点。情境四是情境三的自然延伸,在比较与共性归纳中为几何概型的知识生成铺平了道路。
二、抓住数学本质,创造性地使用教材
基于核心素养的数学教学,要求教师从单一的章节教学中解放出来,以“主题(单元)”作为教学的基本研究对象。主题教学,最重要的是对教材全面把握和进行整体分析。围绕主题教学任务,结合学情分析,确定整体教学流程,设计好每一节课教学内容,在教学实施中不断反思和改进。
例如,在《几何概型》教学中,在概念清晰导出后,精心设计三个例题:
例1 某车站开往广州的大巴每30分钟发车一次,乘客小李到达车站乘车的时刻是随机的,求他候车的时间不多于10分钟的概率。
例2 如图,将一个长与宽不等的长方形水平放置,长方形对角线将其分成A、B、C、D四个区域,在区域中间装个指针,使其可以自由转动,对于指针停留的可能性,下列说法正确的是( )
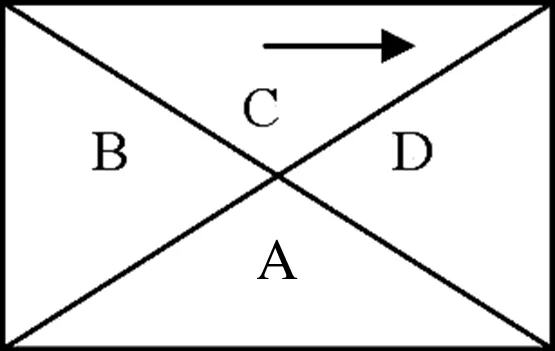
(A) 一样大
(B) A和C区域大
(C) B和D区域大
(D)由指针转动圈数决定
例3 已知平面区域D={(x,y)||x|≤1,|y|≤1},在区域D内任取一点,则取到的点到原点的距离大于1的概率为____
例题1是几何概型的直接应用,由于钟表的表盘一般是圆的,多数学生容易想起用面积、角度或者弧长来求概率。在课堂上展示学生们的各种解法,先让他们各抒己见,再给学生分析所选择几何度量的合理性。重点分析教材的解法——将时间转化成长30的线段,研究事件A位于[20,30]之间的概率。开放性探讨目的是让学生对几何概型的有更深入理解,提高解决问题的能力。例题2则设计了一个陷阱,部分学生会误以为是直接用三角形的面积比,通过此题让学生明白几何概型一样要注意基本事件的“等可能性”和如何合理选择几何度量。例题3就是巩固和提升。
这节课的设计首先是通过对教材问题的改造,用“飞行棋”创设情境,从熟悉的游戏引入,激发了学生的兴趣,创造性使用教材,又为几何概型概念的构建作铺垫。对例1(课本例题)进行了改编,拓宽学生看问题的角度,同时补充了例题2和例题3(课本没有),让学生进行概念辨析,抓住等可能这个概念核心,突破难点,又一次创造性使用了教材。
三、采用变式教学,培养学生抽象意识
抽象是数学的特性。但正是因为这种抽象,使得数学习得和数学应用之间形成了一条鸿沟,所以培养学生抽象意识尤其重要。
在教学中,可以采用一题多解、一题多变、题组变式等方式,由浅入深,引导学生进行辨析对比,探求不同的解题方案。通过这种变式类型的训练来提升学生抽象能力,让学生有意识的抛开事物表象看本质,转化为数学问题,达到强化其抽象意识的目的。
例如,在《利用基本不等式求最值》这节课的教学中,设计下列变式题组:
题组一
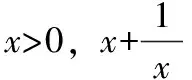
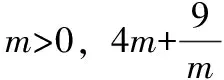
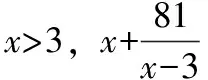
题组二
1.设0 3.设x,y>0,且9x+y=4,xy的最大值为____ 题组三 这三个题组实现了思维上由浅入深,难度层层递进。对于三个题组的第一小题,教师给予适当引导,让学生学会对比,抽象出问题的本质根源,其余的两小题把思考的自主权还给学生,自由讨论,让学生在由易到难的一步步思考中,不断增强抽象意识。 数学是思维的科学,是思维的舞蹈,科学的思维方法尤其重要。教师在数学教学中重视渗透基本的数学思想方法,不但能让学生会做数学,而且还能让他们明白该怎样去思考新问题,用什么方法去解决问题。这些能力的养成,不但在短期发挥作用,它们甚至可以影响学生的一生。 如何在数学课堂无形地渗透数学思想方法是我们教师要研究的大课题。教师不仅要钻研教材教法,研究数学思想方法渗透的方式,设计好上课的教案,还要善于在课堂教学中捕捉渗透数学思想方法的契机。 如在“双曲线”这一节的教学中,教师把握课堂进程,类比椭圆的定义、标准方程和几何性质,逐步展开。课堂上留给学生充分的思考时间,巧妙引导学生类比椭圆去学习双曲线的知识。在探究学习中,让学生明白为什么能类比?为什么要分类?领悟和运用类比方法、数形结合和分类讨论的思想方法。这样,学生从学习中碰撞出数学思想方法的火花,类比、数形结合等数学方法才能植根于学生的头脑中。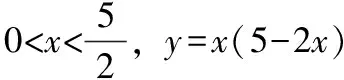
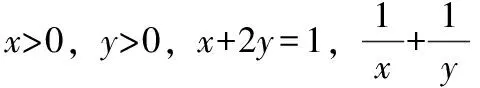
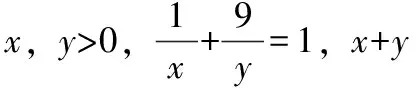
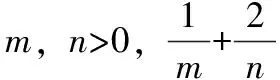
四、渗透思想方法,提高解决问题能力

