落实教材与考纲要求，扎实推进学科素养培养

文/广州市番禺区石碁中学

高考试题的特点一是紧扣考纲，二是贴近教材，三是能力考查。通过对近年高考试题的分析就不难发现，试题的许多题目都能在课本中发现“踪影”，不少试题就是对课本原题的变形、改造或综合，有些题目则是对课本的概念、性质、定理及公理等的直接或间接的考查。在这一背景下也要求我们在紧扣考纲的同时，对课本的知识体系有一个完整的架构。熟悉课本的知识点，对知识点在各章节的功能及作用有清楚的认识；二是对课本的习题，特别是例题要深入研究；三是对知识在跨章节间的联系以及作用不时要有所体现及比较；四是适时对知识进行归纳总结及拓展延伸，以适应新高考对学生数学核心素养及创新能力的要求。

一、强化知识点，落实“三基”

“三基”是指基础知识、基本技能和基本解题方法。知识点落实不到位，可谓“巧妇难为无米之炊”，即使再基本的题型，学生思维是多么的好，也无法解决，或者是思路正确，过程错误，得不偿失。比如，高考考纲中明确要求考生能正确运用三角公式进行三角函数式的化简求值和恒等证明，但有的考生由于公式不熟，导致过程出错。

此题的一般正确解法是先变形再运用透导公式等化简：

=4cos2x

但也有的考生不仔细观察题目特点直接运用和(差)角公式：

还有一种情况是和(差)角公式记错：

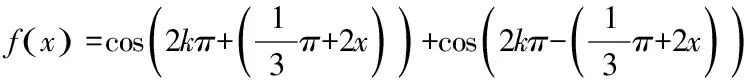
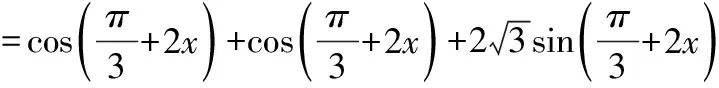
以上两种问题都是由于基础知识不够扎实导致的，在解答题的第一题就出现这样的问题，结果对一些考生的整体成绩产生造成较大影响。

二、依“纲”固“本”，挖掘例题习题的潜在功能

课本知识是几代人集体智慧的结晶，同时经过权威部门由专家学者编著而成，具有很强的权威性、指导性，因此课本知识也是高考必考或者重点考查的内容。

例2.设平面内有n条直线(n≥3)，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用f(n)表示这n条直线交点的个数，则f(4)=____；当n>4时，f(4)=____。(用n表示)

以上例子是曾经的高考考题对教材习题的直接转换或变式。经验告诉我们只有吃透课本上的例题、习题，才能全面、系统地掌握基础知识和基本方法，构建数学的知识网络，以不变应万变。在求活、求新、求变的命题的指导思想下，高考数学试题虽然不可能考查单纯背诵、记忆的内容，也不会考查课本上的原题，但对高考试卷进行分析就不难发现，许多题目都能在课本上找到“踪影”，不少高考题就是对课本原题的变型、改造及综合。回归课本，不是要强记题型、死背结论，而是要抓纲悟本，对着课本目录回忆和梳理知识，把重点放在掌握例题涵盖的知识及解题方法上，选择一些针对性极强的题目进行强化训练、复习才有实效。

三、深化知识，重视知识间的网络建构

高考对知识点的要求是：“系统地掌握知识的内在联系，对所列的知识内容有较深刻的理性认识”，这要求对课本知识不但要整体把握，还要能深入浅出。实现这点必须对知识点不断总结、归纳、分类，以达到知识间的纵横联系。由此，才能在不断创新变化的考题背景中捕捉到出题者的真正意图，考查什么，究竟如何把握试题关键，尽快找到切入点确定解题思路，优化解题过程。

例3.已知a,b,c,d都是实数，且a2+b2=1,c2+d2=1,求证|ac+bd|≤1。

此例可用多种方法来解，体现了综合与分析互为前提、互相渗透、互相转化的辩证统一关系；知识间的相互联系、相互结合、综合运用；一题多解强化知识结构,锻炼发散性思维；运用适当的方法简化解题思路及过程。

四、总结提炼，拓展延伸

历年高考数学中都突出对数学知识主干的考查，重点以知识构建试题的主体，在代数部分着重考查函数、数列、三角函数等内容，立体几何以各种立体图形为载体，主要考查两条异面直线所成的角、点到平面的距离和二面角的求法，解析几何还是以求轨迹为前提、围绕直线和圆锥曲线的位置关系这一重点来设计试题，而且就试卷整体来说，重点考查向量与三角、向量与立体几何、函数与导数、数列与导数、概率统计等。既然有迹可寻，这就要求对各类知识点进行归纳总结，梳理好知识脉络，进行知识点与解题方法的总结、提炼以提高效率。

为了适应高考考试对知识及能力的要求，还须对课本知识进行拓展延伸，以充分发挥教材的应有功能。如在人教版高中数学必修教材中的等差数列前n项和公式推导中，可以总结及拓展数列求和的常用方法：

1.公式法：适用于等差、等比数列或可转化为等差、等比数列的数列。

2.分组求和法：将根据数列特点将数列分解或变式成某两类或更多同类别的数列，再分别求，再累加。

4.错位相减法：适用于{anbn}其中{an}是等差数列，{bn}是各项不为0的等比数列。

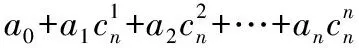
6.构造法：根据题型特点，通过变式改造，将原数列变成满足等差或等比数列定义式的形式，直接求和或变式转换求和。

……

从历年的高考试题中可以看出，无论是以往的广东卷还是全国卷，在求数列前n项和中大多采用以上所列方法。