异步牵引电机冷热态转矩控制策略

王龙刚,苏鹏程,牛剑博

(中车永济电机有限公司，西安 710018))

0 引 言

基于转子磁链定向的间接矢量控制以其控制简易、动静态性能优越等优势在机车牵引控制领域有着广泛的应用。但是该方法的磁场定向依赖电机参数，尤其是转子电阻值的变化。按照机车牵引变流器和牵引电机组合试验标准[1]，在全速度范围内，要求牵引电机冷热态的输出转矩与技术要求的偏差都在±5%以内。如何减小转子电阻对控制性能的影响，保证电机冷热态输出转矩都在偏差之内，是组合试验电机特性调试的难点和重点。

1 原理分析

1.1 转子磁链定向的间接矢量控制

图1是基于转子磁链定向的间接矢量控制框图。

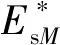
图1 基于转子磁链定向的间接矢量控制

间接矢量控制的同步频率ωs是通过电机转速ωr加上式(1)计算的滑差频率，因此，间接矢量控制也被称为转差型矢量控制[2]。

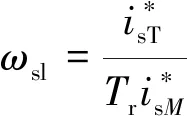
(1)

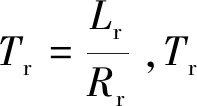
基于转子磁链定向的间接矢量控制策略，是以转子磁链矢量ψr来定向的。需要确定ψr的瞬间空间大小和位置，对运行参数的指令值和实际检测值进行数学运算，并以此来实现励磁分量和转矩分量的解耦。

间接矢量控制的转子磁链ψr计算公式有电压和电流观测模型两种。

电压观测模型计算公式如下：

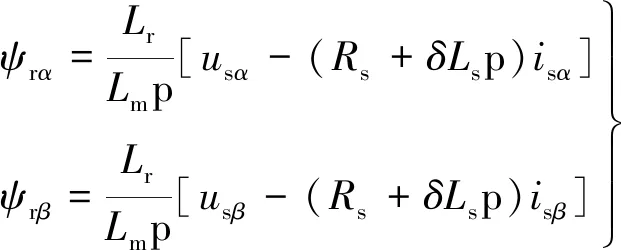
(2)

式中：ψrα,ψrβ为转子在α,β坐标系的磁链；Lm，Ls，Rs分别为励磁电感、定子电感、定子电阻；usα，usβ为定子在α,β坐标系的电压；isα，isβ为定子在α,β坐标系的电流；p为微分算子；δ为漏磁系数。

式(2)的电压观测模型计算磁链大小不涉及到电机转子电阻的参数，受电机冷热态的影响很小。由于电压模型存在积分环节，在低速运行时，模型运行困难。

电流观测模型计算公式如下：

(3)

式(3)的电流观测模型用到的转子时间常数Tr，随着转子绕组温度而变化，会影响磁链观测器的准确性，甚至影响整个矢量控制系统的性能。另外，采用电流模型法时，由于存在一阶滞后环节，在动态过程中，难以保证控制精度。

在实际控制系统应用时，一般采用电压模型法和电流模型法相结合的磁通观测模型，如下：

(4)

式中：ωc，s分别为截止频率、拉普拉斯算子。

通过设置合理的截止频率ωc，在低速时电流模型起作用，高速时电压模型起作用，可实现两个模型的平稳过渡[3]。在机车的全速度范围内，低转速运行时，多个方面参数都会影响到磁链观测的精度，因此实际采用磁链开环[5]；在高转速区，调制进入方波，这时磁链轨迹与圆形差别较大，也采用磁链开环[6]；在低速到方波之间采用式(4)的磁链观测模型，一般截止频率ωc设置较低，电流模型在磁链闭环作用区间占很小比例。因此，在磁链闭环速度范围内，转子电阻值变化时，认为磁链ψrα，ψrβ幅值不变化。

图1中，间接矢量控制的转子磁链ψr空间位置，是转速ωr加上转差频率ωsl的积分：

(5)

转速测量准确时，转子磁链ψr的准确定向与转差频率的计算相关。

在计算得到静止坐标系转子磁链ψrα，ψrβ，如式(6)，经过Park坐标系变化，得到M，T坐标下的转子磁链ψrM,ψrT。

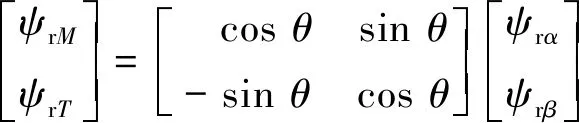
(6)

转子磁链空间大小和位置都观测准确时，ψrT=0。

对比以上分析，实际转子电阻值变化时，对于磁链幅值ψrα和ψrβ影响很小，但会导致θ角度定位不准确。在进行Clarke变换，计算得到ψrM和ψrT不准，引起转矩控制性能的下降。

1.2 冷热态输出转矩分析

以下带上标符号表示电机热态数据,无上标表示电机冷态数据。

图2 牵引工况转子磁链矢量图

图3 制动工况转子磁链矢量图

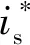
1.3 转子磁链定向角度补偿

对于基于转子磁链定向的间接矢量控制系统，随着转子电阻值增大会导致转子磁链定向不准，牵引工况时输出转矩减小，制动工况时输出转矩增大。依据前面分析，通过补偿转差频率，可以减小转子磁链定向误差，提高热态的控制性能。对于机车全速度范围，磁链开环和闭环采用不同的补偿频率方式。磁链闭环，采用T轴磁链的模型参考自适应系统磁场定向角度校正方法；磁链开环，采用电机温升ΔT补偿转差频率的方法。控制框图如图4所示。

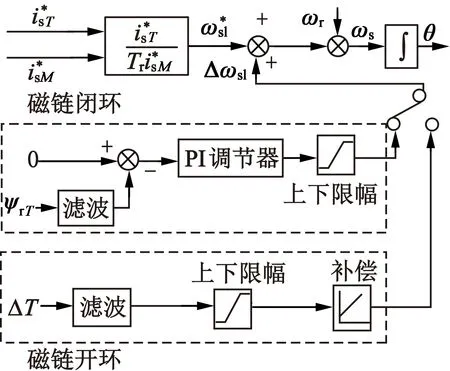
图4 全速度转差频率补偿

在磁链闭环控制时，磁链观测模型计算的T轴角度滞后于实际磁链角度，这时角度误差为负值，磁链观测模型计算的T轴磁链ψrT为正值，经过PI调节器后，补偿转差频率为正值，同步频率增大，使得估算T轴角度跟踪上实际转子磁链矢量的角度。反之，当角度误差为正值时，磁链观测模型计算的T轴磁链ψrT为负值，经过PI调节器后，补偿转差频率为负值，同步频率减小，使磁链定向角度误差逐渐减小到零，实现磁场的准确定向。另外，基于T轴磁链的模型参考自适应系统磁场定向角度校正方法，不受其他电机参数的影响。

程序中给定的转子电阻一般都是冷态下测量参数，在电机运行过程中，实际转子电阻值会随着温度升高而逐渐增大，实际磁链逐渐超前。所以磁链开环时，根据电机温升ΔT的增大，通过补偿转差频率，可减小转子磁链定向角度的误差。

2 试验测试

2.1 冷态测试数据

图5是某型号牵引变流器与电机的冷态转矩试验数据曲线。

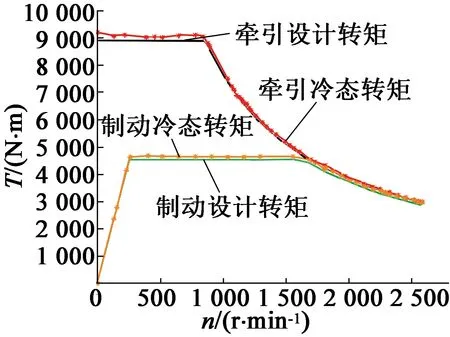
图5 电机牵引/制动冷态转矩曲线

在全速度范围内，牵引/制动工况，电机冷态实测和设计要求转矩偏差都在±5%的偏差范围内[1]。

2.2 热态测试数据

由于电机转子的温度不容易直接测量，试验中将定子铁心温升Δt作为参考，实际数据铁心温升为非均匀的散点。

如图6所示，X轴为实测与冷态测试转矩的差值，Y轴为电机转速，Z轴为铁心温升Δt。表1是牵引工况转速1 185 r/min时，温升过程中的实测转矩，设计力矩6 447 N·m。

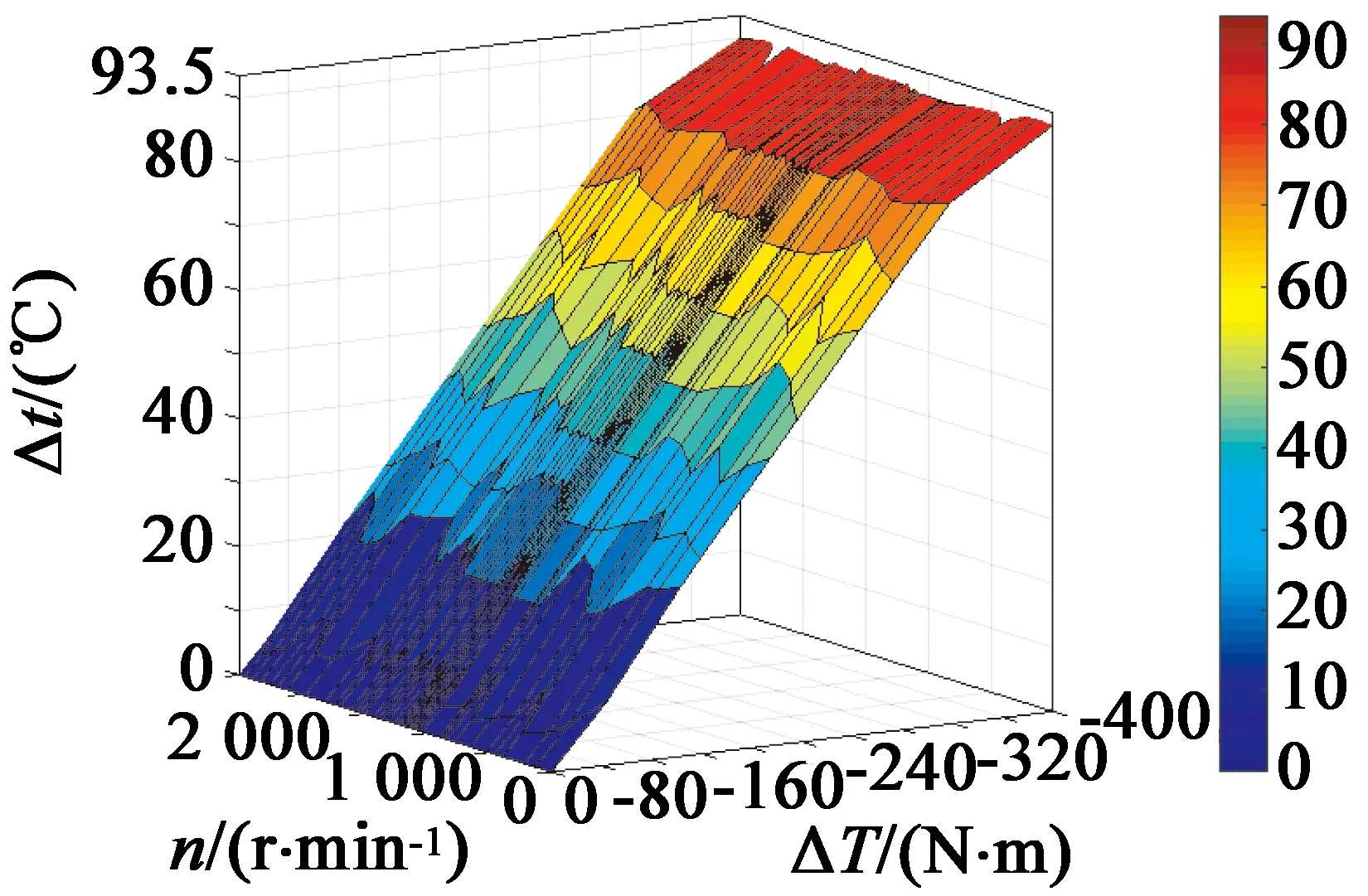
图6 牵引工况时热态转矩数据表1 牵引工况转速1 185 r/min热态转矩值

温升Δt牵引/℃与冷态转矩差值ΔT/(N·m)实测力矩T/(N·m)与技术要求偏差/%006 591+2.25.6-416 550+1.621-786 513+1.031-1376 454+0.144.5-1546 437-0.256.5-2076 384-1.065.8-2386 353-1.574.5-2846 307-2.279.4-3176 274-2.789.5-4006 191-4.0

从图6可以看出，随着铁心温升Δt牵引增大，全速度范围实测力矩值都在减小。表1中转速1 185 r/min，冷态时实测力矩与技术要求偏差为+2.2%，当铁心温升Δt牵引= 89.5 ℃时偏差为-4.0%，冷热态最大力矩偏差达6.2%。

图7为制动工况下热态力矩数据。

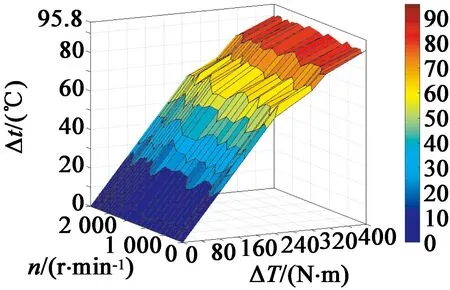
图7 制动工况时热态转矩数据

表2是制动工况转速1 033 r/min时，温升过程中的实测转矩，设计力矩4 540 N·m。

图7中，随着铁心温升Δt制动增加，全速度范围实测力矩值逐渐增大。表2中转速1 033 r/min，冷态时实测力矩偏差为+2.2%，当铁心温升Δt制动= 90 ℃时偏差为11.2%，当铁心温升Δt制动>43.8 ℃，实测力矩偏差已经超出±5%。

表2 制动转速1 033 r/min热态转矩值

从实测数据可以看出，随着电机铁心温度升高，牵引工况下，力矩输出逐渐降低，制动工况下逐渐增大，与本文理论分析的结果一致。

2.3 补偿后热态测试数据

按照转差频率补偿的方法，对于磁链闭环时，采用T轴磁链的模型参考自适应系统磁场定向角度校正[5]；磁链开环，根据电机温升Δt补偿转差频率。

图8是补偿后，牵引工况测试的热态力矩数据。

图8 补偿后牵引工况时热态转矩数据

表3是牵引工况，转速1 185 r/min，温升过程中补偿后的实测转矩。

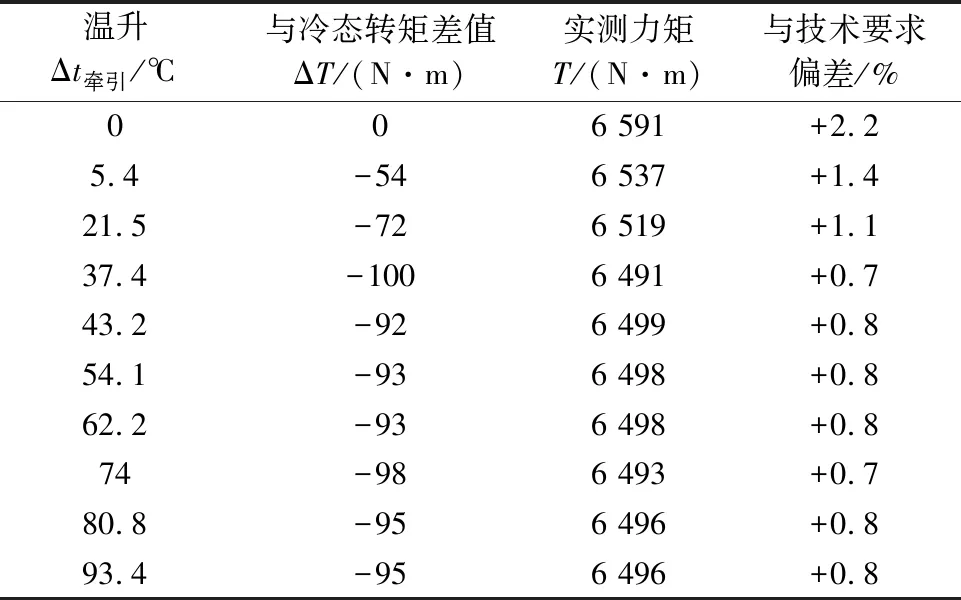
表3 补偿后牵引工况转速1 185 r/min热态转矩值

从图8可以看出，随着铁心温升Δt牵引增大，全速度范围实测力矩值也在减小。表3中转速1 185 r/min，冷态时实测力矩与技术要求偏差为+2.2%，当铁心温升Δt牵引= 93.4 ℃时偏差为+0.8%，冷热态最大力矩偏差为1.4%。

图9是补偿后，制动工况测试的热态力矩数据。

表4为制动工况，转速1 033 r/min，温升过程中补偿后的实测转矩。

从图9可以看出，随着铁心温升Δt制动增大，全速度范围实测力矩值逐渐增大。表4中转速1 033 r/min，冷态时实测力矩与技术要求偏差为+2.2%，当铁心温升Δt制动= 92 ℃时偏差为+4.1%，冷热态最大力矩偏差为1.9%。在全速度的温升范围内，力矩偏差都在±5%以内。

图9 补偿后制动工况时热态转矩数据表4 补偿后制动工况转速1 033 r/min热态转矩值

温升Δt制动/℃与冷态转矩差值ΔT/(N·m)实测力矩T/(N·m)与技术要求偏差/%004 640+2.29.9254 665+2.819.2454 685+3.234544 694+3.443.2644 704+3.654.5834 723+4.063.2854 725+4.172.1874 727+4.182.9854 725+4.192844 724+4.1

采用全速度范围内补偿转差频率后，牵引工况1 185 r/min速度点，冷热态力矩最大偏差从6.2%降为1.4%；制动工况1 033 r/min速度点，冷热态转矩最大偏差从11.2%降为1.9%。牵引系统的转矩控制精度提高。

3 结 语

根据实测试验数据，对于基于转子磁链定向的间接矢量控制系统，无论磁链开环还是闭环，都是随着转子电阻值增大，牵引输出转矩减小，制动输出转矩增加。采用全速度范围转差频率补偿后，能有效减小冷态和热态转矩的误差，使牵引电机的冷热态输出力矩都在技术要求的范围内。另外，采用转差频率的补偿方法，既能够保证转矩输出精度，又不会增加电机的损耗，优于补偿转矩分量的方法。