两相整距绕组双凸极永磁电机等效磁路模型

周智庆,龙庆文,叶树林, 田 英

(1.佛山科学技术学院，佛山 528225; 2.广东交通职业技术学院,广州 510650)

0 引 言

定子永磁式的双凸极永磁电机因其结构简单、可靠性高、功率密度大等优点，持续获得了广泛的关注，一般地采用集中绕组缠绕于定子凸极上，也即集中绕组式双凸极永磁(以下简称DSPM)电机[1-5]。然而，DSPM电机存在明显的扭矩波动，其扭矩波动与若干因素有关[6]，包括：相绕组电流是否为线性、永磁磁场波形、相电流开关导通角以及绕组电感等，这使得DSPM电机控制策略和系统变得复杂，成本增加和可靠性降低。为了解决扭矩波动的问题，文献[7]提出了一种整距绕组双凸极永磁电机(以下简称FMDSPM)，验证了其具有更低的输出扭矩波动水平，同时具有更高的能量密度，而在定转子结构一样的情况下，相数更少，控制简单，可靠性高，成本更低。

在文献[8]中，给出了DSPM电机变网络等效磁路模型，显示了其有效性和计算效率；相比较有限元法，等效磁路法具有计算量小、计算快的显著特点，可以帮助设计者在电机设计和特性分析初期阶段节约大量时间、提高研究设计效率，又能获得可参考的计算精度[8-10]。和DSPM电机不同，两相FMDSPM电机采用整距绕组，尽管定转子结构和DSPM相同,但其等效磁路模型中的电磁转换部分和DSPM有明显不同。

本文以一台6/4极FMDSPM电机为例，给出其等效变参数磁路模型，通过迭代计算获得其磁链，反电动势以及槽扭矩等静态参数，并与有限元分析法比较，确证结果的可参考性。

1 FMDSPM电机的磁路模型

图1为6/4极FMDSPM电机结构图，包括A和B两相绕组，每相绕组为整距绕组结构，对应着A相绕组电感最大而B相绕组电感最小的状态。图2为FMDSPM电机的1/2等效磁路模型，绕组等效磁动势源(MMF11，MMF12，MMF21，MMF22)与定子轭部等效磁导串联，而DSPM电机等效磁路中绕组等效磁动势源位于定子极中，与定子极等效磁导串联，由于定转子结构和DSPM电机一样，磁路模型中其他部分两者相同。图2中：spolep1，spolep2，spolep3，spolen1，spolen2，spolen3为定子极等效磁导；syokep1，syokep2，syoken1，syoken2为定子轭部等效磁导；Rslot11，Rslot12，Rslot13，Rslot21，Rslot22，Rslot23为定子极间等效漏磁导；Rg11，Rg12，Rg13，Rg14，Rg21，Rg22，Rg23，Rg24为气隙等效磁导；Ryoke1，Ryoke2，Ryoke3，Ryoke4为转子轭部等效磁导；rpole1，rpole2，rpole3，rpole4为转子极等效磁导；pm1和pm2为等效永磁源；Rl11，Rl12，Rl21，Rl22为定子永磁体两侧的等效漏磁导。

图1 FMDSPM电机结构示意图

图2 FMDSPM等效磁路网络模型

永磁磁通源及其两端的等效漏磁导和定转子铁心等效磁导以及定转子铁心完全重合时的边缘漏磁导的计算方法在文献[10]中已有赘述，此处省略；主要就气隙的变参数等效磁导计算方法进行分析。

磁导计算遵循磁通管理论，为使问题简单化，将定转子之间的气隙划分为5个部分，如图3所示,分别为定子侧面到转子极面的区域3和4，定子极面到转子侧面的区域5和6，以及重合气隙的区域0。

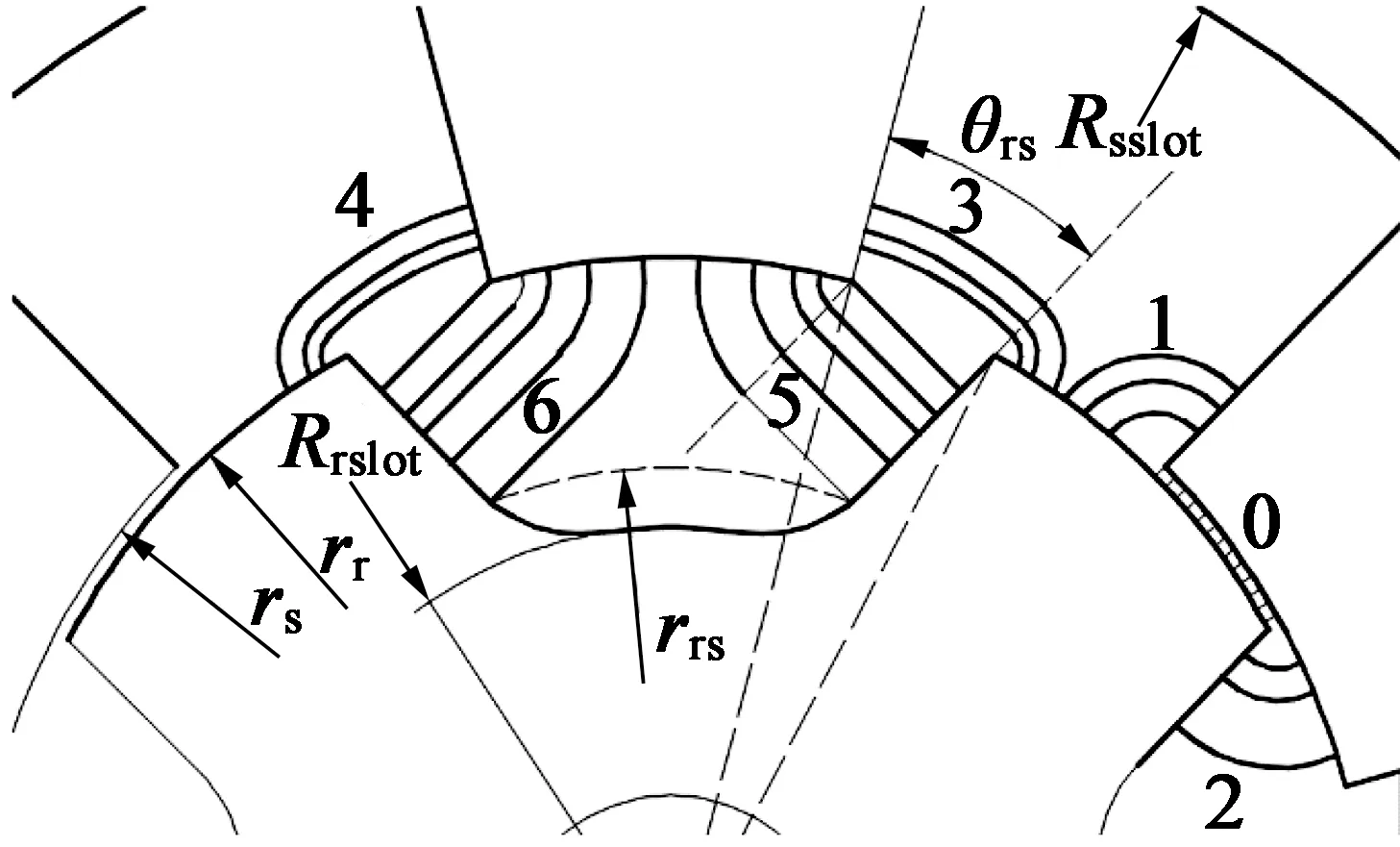
图3 气隙磁导区域分布图

定转子极弧重合的气隙磁导率：

(1)

式中：Rp为定转子极面重合度系数，Rp=θrt/θM，θrt为定转子磁极的实时重合角度；θM为定转子重合的最大角度；μ0为真空磁导率；l为轴向长度；g为气隙长度，g=min (θs,θr)，θs,θr分别为定转子极弧宽度；rs,rr分别为定子和转子铁心内径和外径。

非重合位置如图3所示，定子极面和转子侧面之间的等效气隙磁阻：

式中：θrs为定子极侧面与相向的转子极侧面之间的夹角；θss为定子极侧面与定子内径面之间的夹角；rrs取决于转子轭部外径rrslot大小和定转子极的相对位置，定转子凸极非重合时，rrs取值条件如下：

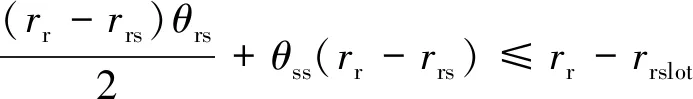
(3)

定转子凸极重合时，在满足式(3)条件的同时，也要满足以下约束条件：

同理,把式(2)中的rr-rrs替换成rss-rs，就可得到定子侧面与转子极面之间的等效气隙磁阻Rssrp1。rss受定子轭部内径和定转子极相对位置的影响，取值约束条件：

(4)

同理，根据式(2)～式(4)，可求得定转子极另一侧区域4和6的等效气隙磁阻Rsprs2和Rssrp2，进一步引入转子凸极与定子槽的重合度：

(5)

式中：θst为转子极与定子槽实时的重合角度；θslot为定子槽最大开口角度。

根据转子极通过定子极的规律，结合式(2)～式(5)，得到非重合位置的总磁导:

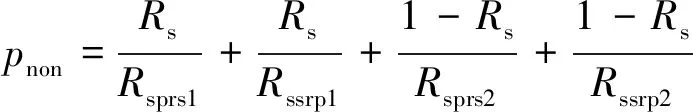
(6)

最后，获得定转子极的总磁导：

pall=poverlap+pnon

(7)

随着转子转动，通过改变气隙参数，区域5和6变成区域2，区域3和4变成区域1，从而无需改变等效磁路网络，通过改变磁路模型中相应磁路原模型参数就可以得到新转子位置时的等效磁路模型。

2 模型求解

随着转子转动，产生新转子位置状态，电机磁路参数在变化而不是磁路网络在变化，随着磁路网络参数的变化，快速进行迭代计算。根据磁路和电路相似性理论，将电路节点矩阵求解方法应用于磁路网络求解中，则：

(8)

式中：n为磁路网络的节点数；F(k)表示在节点k处的相应磁动势；ψ(k)表示流入磁路网络中节点k等效磁通量代数和。当k1=k2时，P(k1,k2)为连接到点k1各磁路磁导的总和；当不相等时，P(k1,k2)为连接到两点之间磁路磁导之和的负数。根据式(8)求得相应节点的磁动势值，可进一步确定每个支链的磁通。

3 特性分析

3.1 磁链

通过求解，得到电机定转子各部分段的磁通，尽管绕组处于定子槽中，然而，单相绕组的磁链依然根据定子极中的磁通获得，从而：

(9)

等效磁路法计算的A相绕组磁链结果示于图4中，同时也给出了有限元计算结果。对比显示，两种方法计算结果基本吻合，等效磁路法得到的结果略小，后面的反电动势分析显示，该误差是可以接受的。

图4 A相绕组磁链(转子转速1 000 r/min)

3.2 反电动势

反电动势由磁链求导得到，即：

(10)

磁链的误差也反映到反电动势上，如图5所示。在10 ms以后，两种方法计算的反电动势特征一致，但是数值存在误差，在电机初期设计论证阶段，这个误差对基本特征的评估影响可忽略。误差的来源在于磁场的空间分布非常不均匀，从而造成了等效磁路模型中的磁导更小。

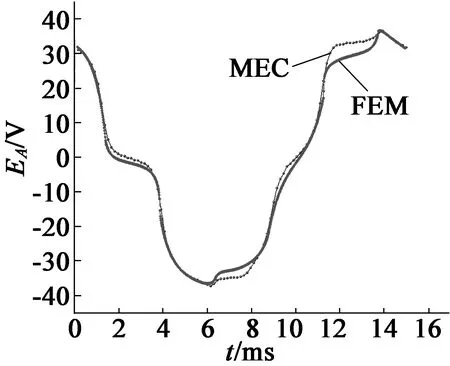
图5 A相绕组的反电动势(转子转速1 000 r/min)

3.3 齿槽转矩

齿槽转矩是永磁电机的固有现象，对于定子永磁型双凸极电机同样存在槽扭矩现象。槽扭矩是永磁场与定转子铁心在相对运动过程中相互作用的结果，实际上是一种磁阻性扭矩，对电机性能输出存在比较大的影响。对FMDSPM槽扭矩求解，通过进入定子侧面的切向磁通分量求解得到[11]：

(11)

式中：Bi1,Bi4分别表示第i个定子齿左右两边磁路的磁通密度；ai1,bi1分别表示第i个定子齿左边磁路边界到该齿距离最近和最远极限值；ai4,bi4分别表示第i个定子齿右边磁路边界到该齿距离的两个极限值。

图6示出了等效磁路法和有限元法槽扭矩计算结果，峰值正负都在400 mN·m左右。两种方法对槽扭矩的计算结果形状也基本吻合，但由于对磁路非线性的处理差别导致些许误差，说明了等效磁路法在精度上不如有限元法，但是得出的基本结论是正确的，这也是发展等效磁路法的初衷，也即，显著缩短电机设计过程中初期论证所消耗的时间。

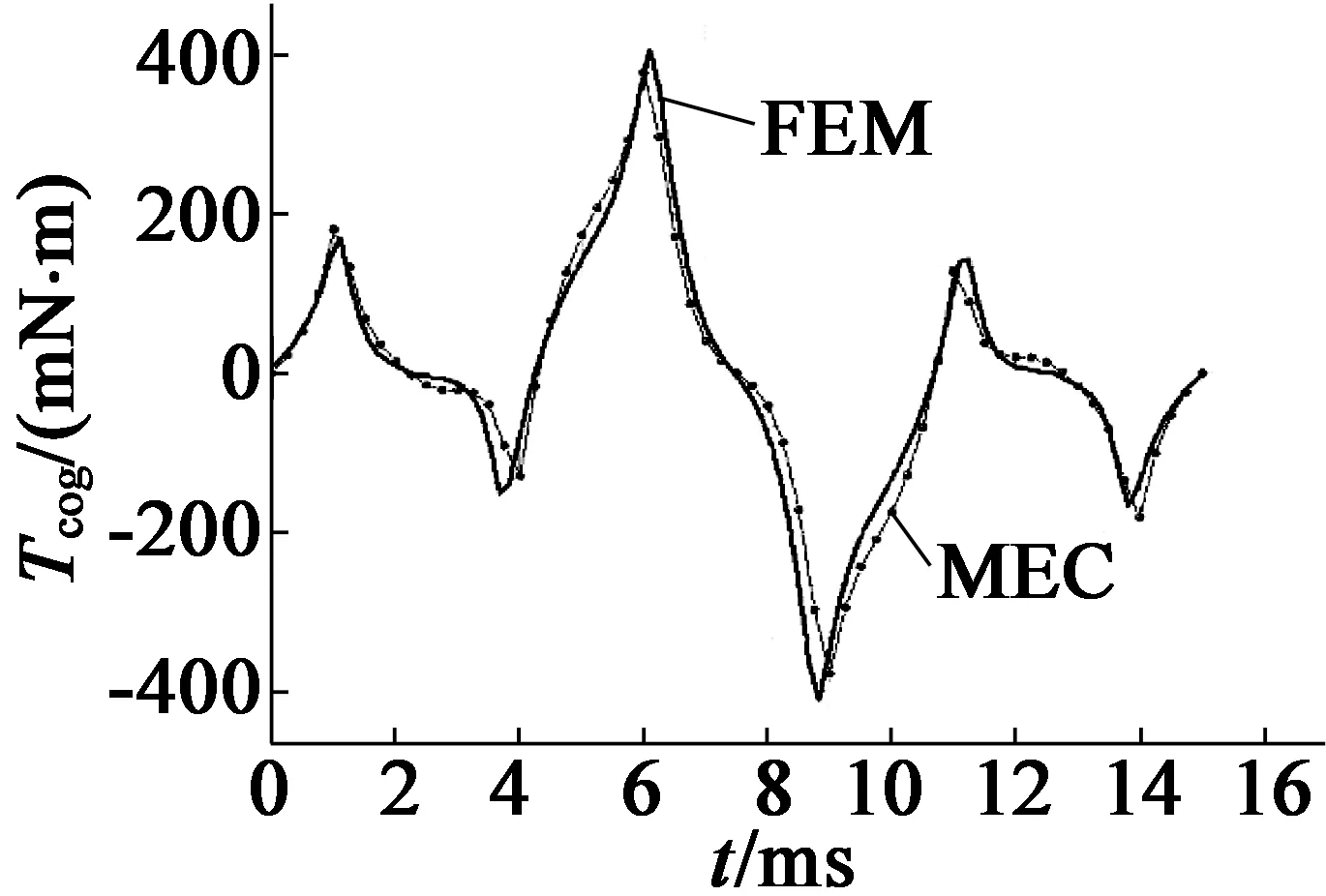
图6 齿槽转矩

4 结 语

与现有集中绕组DSPM电机相比，整距绕组DSPM电机具有高绕组、高空间利用率以及高扭矩密度的突出特征，作为一种新型电机，在进入设计定型之前需要做大量的分析论证工作。

本文建立了FWDSPM电机等效磁路模型，有利于初期设计论证快速进行；在一个电周期内分析得出的磁链、反电动势和齿槽转矩结果显示，五分区法等效磁路模型输出结果整体上和有限元法得出的结果基本吻合，不足之处是在一些局部突变部位存在些许误差，有待进一步改善。