鲇鱼山灌区渠首除险加固输水能力研究

张文峰，李西平，黄绍磊，李 璐

（1.河南省水利勘测设计研究有限公司，河南 郑州450016；2.河南省水利勘测设计协会，河南郑州450016）

1 工程概况

鲇鱼山灌区取水枢纽位于河南省商城县鲇鱼山水库大坝下游4 km的灌河河道上，灌区设计灌溉面积9.53万hm2。现状渠首由进水闸、冲沙闸、溢流坝（堰）等建筑物组成。进水闸最大流量为119.2 m3／s，冲沙闸最大流量为728 m3／s，溢流坝原规划最大输水流量为3 940 m3／s。鲇鱼山灌区取水枢纽运行40 a来，为灌区提供了充足水源，促进了灌区耕作制度和种植结构调整，带动了相关产业快速增长。但受当时社会发展水平制约，原设计闸墩、底板配筋不能满足现行规范要求。

2 原设计方案的问题

鲇鱼山灌区取水枢纽1970年开始动工，1976年正式建成。查阅当年竣工资料，其进水闸、冲沙闸中墩和底板配筋均为Φ16＠300，满足当时规范［1］中受拉、偏心受压构件的受拉钢筋最小配筋率（0.15%）的要求，但按照当前有效规范《水工混凝土结构设计规范》（SL／T 191—2008）［2］，受拉、偏心受压构件的受拉钢筋最小配筋率为0.2%，相应该工程中墩配筋应为Φ20＠200，底板配筋应为Φ25＠200。因此，原设计闸墩、底板配筋不能满足现行规范要求。

其壅水计算采用天然河道一维恒定非均匀流方法，起推水位为溢流坝前水位，5 a一遇设计洪水位为78.2 m，依据最新实测河道资料，经过计算，5 a一遇洪水对应淹没点水位为79.34 m，而淹没点岸边高程仅为78.4 m，当发生小频率洪水时，易发生回水倒灌，发生漫溢。经初步统计，当发生5 a一遇洪水时，淹没面积约2.8 km2，受灾人口500余人、房屋700多间，连接鲇鱼山水库管理所与商城县县城的公路亦将遭受淹没，影响水库运行管理、调度和周围百姓正常生活。

鉴于原设计的问题，2017年河南省水利厅组织有关专家对其进行了安全鉴定，基于河南省水利勘测设计研究有限公司的《鲇鱼山灌区取水闸枢纽工程安全评价报告》及安全鉴定结论，本文对其除险加固后渠首的输水能力进行了研究。

3 除险加固方案

鲇鱼山灌区取水枢纽工程主要技术参数不能满足规范要求，安全等级为C级，依据《水闸安全评价导则》安全类别评定标准，渠首枢纽闸鉴定为四类闸，需报废重建［3］。

由于原渠首布置合理，建成之后各个建筑物过流能力正常［4］，因此除险加固的思路是：原平面布置不变，对进水闸、冲沙闸进行拆除重建；为解决发生低频率洪水时出现回水倒灌的问题，新建左岸泄洪闸；同时新建检修交通桥。

除险加固渠首平面布置见图1。

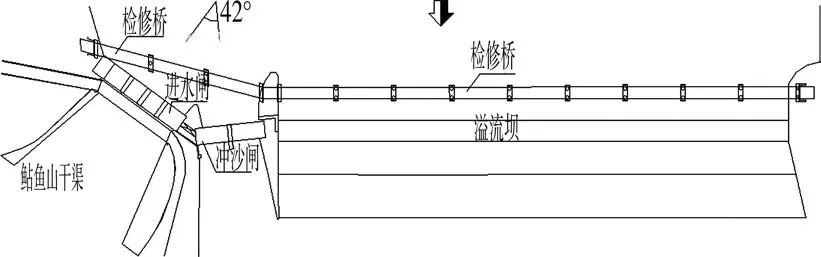
图1 灌区除险加固渠首平面布置

该灌区溢流坝结构安全鉴定为B级，需进行裂缝处理，堰顶高程为77.47 m，上游设计水位为 81.92 m，堰前水深为4.45 m（见图2）。新建检修桥距溢流坝上游12 m，桥宽6 m，桥梁跨度20 m，即每两节溢流坝分缝处设置一个桥墩，下部桥墩为圆形结构，直径1 m。所建的桥梁连接枢纽左右岸，为方便两岸连接及减小其对建筑物结构和过流的影响，所建桥梁在枢纽右岸溢流坝与冲沙闸交界处设一折线，其折线在裹头处完成。

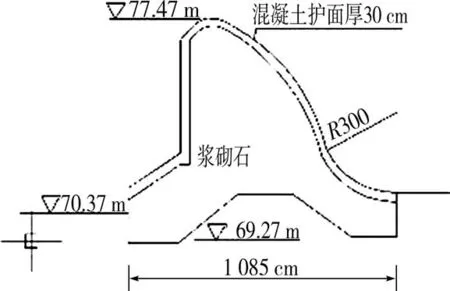
图2 溢流坝断面

新修检修桥距离堰前12 m，约为堰顶水头的2.68倍，不满足距上游堰壁3～4倍堰前水头的要求［5］。在堰前水头影响范围内建设桥梁对溢流坝输水能力的影响目前少有研究，有必要进行深入分析。

4 输水能力计算分析

鲇鱼山灌区溢流坝的堰前水头不包括行近流速水头［5］。根据该溢流坝设计结构，堰顶宽度δ为3.2 m，设计堰顶水头 H 为 4.45 m，δ／H＝0.72，0.67＜δ／H＜2.5，结合设计形态（图2），可判别其为曲线形实用堰。虽然曲线形实用堰的输水能力计算有常规的理论计算公式，但常规理论计算要求的边界条件一般很难保证。根据鲇鱼山灌区取水枢纽新修检修桥后的情况，对其输水能力计算采用了常规水力计算、非均匀流计算、水动力数值模拟计算3种方法，以便相互对比、验证。

4.1 常规水力计算

检修桥设在溢流坝上游，结合该工程实际情况，根据堰顶宽度和最大输水能力对应的堰前水深，溢流坝流态为实用堰流态，输水能力按照《溢洪道设计规范》中公式［6］计算。经计算，建桥前溢流坝实际最大输水流量为4 241 m3／s；将桥梁建在溢流坝上后，溢流坝最大输水流量为3 816 m3／s。

4.2 非均匀流计算

首先按天然河道为非均匀流计算上游桥梁阻水引起的水位落差，然后根据水位降落后的数值，按溢洪道设计规范推荐的公式计算溢流坝输水能力。计算得到溢流坝最大输水流量为4 100 m3／s，比建桥前的（实际最大输水流量4 241 m3／s）略小。

4.3 水动力数值模拟计算

溢洪道水流问题和水利枢纽的水流问题，常需制作水力模型进行研究［7］，这是解决复杂工程课题的重要手段。但模型试验一般难以满足全部相似条件，且模型制作成本高，时间周期长。随着科学技术的进步，许多模型试验可以采用计算机数值模拟来替代，采用数值模型是对传统物理模型的丰富和补充，同时可大大提高效率、降低成本。笔者采用数值模拟方法对建桥后的溢流坝水力特性进行了研究。

4.3.1 基本控制方程

基本控制方程［8］为连续性方程、动量守恒方程和k-ε方程。

连续性方程为

式中： xi为坐标分量（ i＝ 1，2，3）；ui为速度分量。

动量守恒方程为

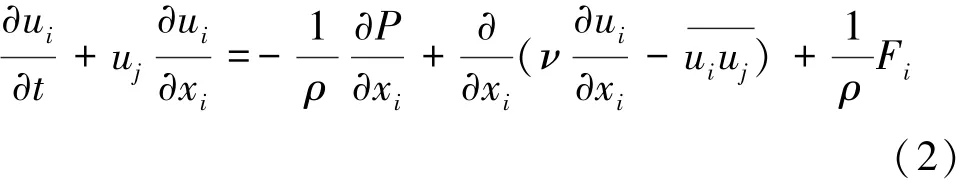
式中：uj为流体的速度分量；t为时间；P为平均压力；ρ为水的密度；ν为流体的运动黏度；Fi为作用于单位质量水体的体积力。

k-ε方程如下：

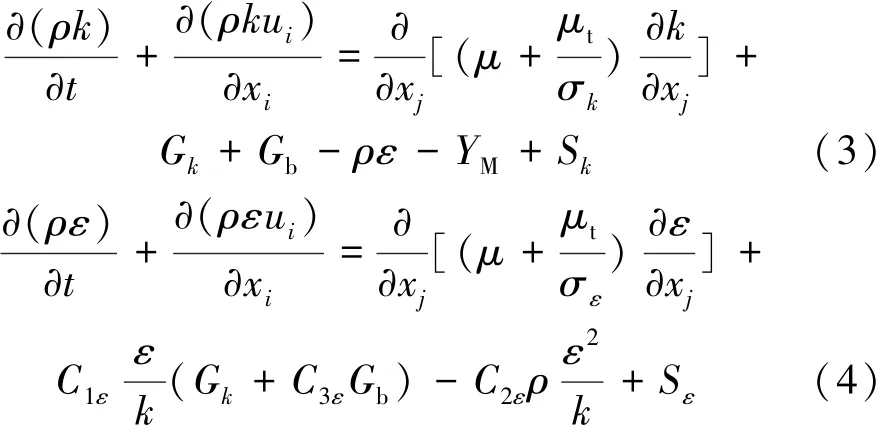
式中：k为紊动能；μ为黏性系数；xj为坐标分量；ε为耗散率；σk、σε为湍动能和耗散率下普朗特数；Gk为平均速度梯度引起的湍动能；Gb为浮力引起的湍动能；YM为可压缩湍流脉动膨胀对总耗散率的影响；Sk、Sε为用户定义的源项；μt为湍流黏度； C1ε、 C2ε、 C3ε为模型常数。

4.3.2 计算方法

计算方法采用当前水力学应用较为广泛的有限体积法，该方法是求解不可压缩、黏性、瞬变和具有自由面流动的流体特性的一种数值方法。计算时对每一相引入体积分数变量αq，通过求解每一控制单元内体积分数值确定相间界面。

计算中所有控制单元表面体积通量的计算采用隐式差分格式，即

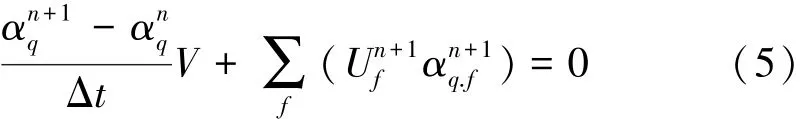
式中：n+1为当前时间步指示因子，n为前一时间步指示因子；t为时间；αq.f为单元表面第q相体积分数计算值；V为控制单元体积；Uf为控制单元表面体积通量。

离散格式采用二阶迎风格式，压力 -速度耦合采用压力校正法，时间差分采用全隐格式。

4.3.3 计算区域、边界及网格划分

数值模拟计算区域包括上游河道（长170m，距坝轴线170m断面为模型上游边界）、溢流坝、冲沙闸、进水闸、消力池、海漫、防冲槽、下游河道（长200m，距坝轴线200m断面为下游边界），分为建桥前和建桥后两种模拟工况，建桥前计算模型见图3。根据工程实际，分析了多种水位组合后确定以对工程防洪作用意义较大的设计水位为典型进行分析，设计上游水位为 81.92m，相应下游水位为79.0m，河道和建筑物边界采用无滑移边界。

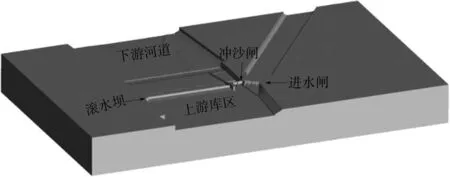
图3 建桥前计算模型

由于该工程在空间上相对比较规则，网格划分选择一般结构网格，上、下游河道和建筑物均采用立方体网格，溢流坝、水闸网格长度为0.25m，上、下游河道网格长度为1m，网格总数约1170万个。

4.3.4 水力模拟输出结果

本次数值模拟采用的是整体水利枢纽模型，可以得出各个建筑物在不同重现期时数值模拟计算结果，其中50a一遇洪水时各建筑物数值模拟输水能力见表1。

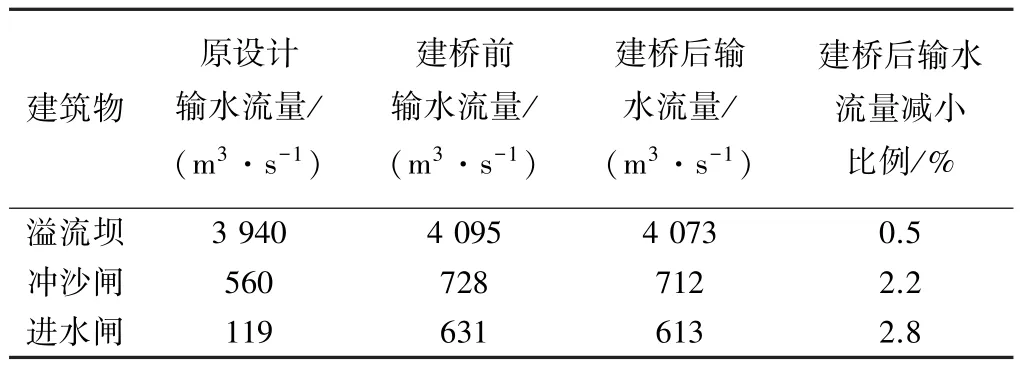
表1 各建筑物数值模拟输水能力对比

由表1可知，虽然建桥后各个建筑物输水能力有不同程度的衰减，但衰减率均小于3%，因此仍能满足原设计过流能力要求。

5 综合分析

将溢流坝公式计算、非均匀流计算以及数值模拟计算输水能力进行对比分析，见表2。

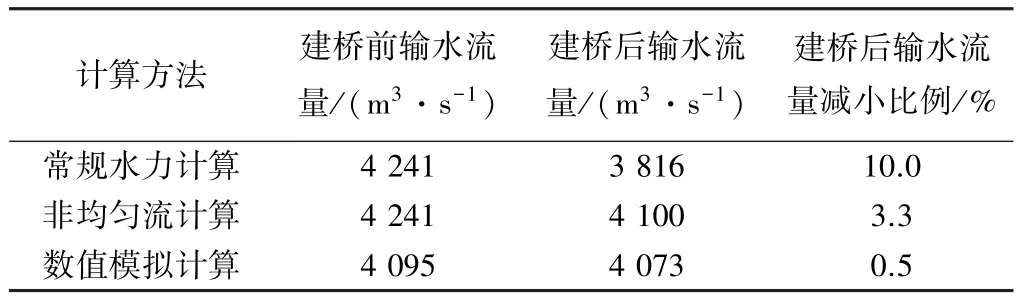
表2 溢流坝公式计算、非均匀流计算及数值模拟计算结果对比

常规水力计算的优点在于所得数值具有普遍性，但该工程溢流坝输水流量常规水力计算值是在假设将桥梁修建在溢流坝上计算的，其结果只能作为对其他计算方法的参考。

按非均匀流计算溢流坝输水能力时，其堰上水头来源有理论依据，但其水头不能满足一般堰流计算的要求，尚缺少理论支撑，其结果亦只能作为参考。

水动力数值模拟计算相当于采用数值方法进行了一次模拟试验，计算区域相对较大，边界条件与实际情况更为接近。数值模拟结果大于公式计算结果、小于非均匀流计算结果，认为将其作为设计依据更加合理。

根据已建好的数值模型及其边界条件，继续研究了在溢流坝上游不同位置（0、4、8、12m）建桥时对溢流坝输水能力的影响，结果见表3。

可见，在溢流坝上游0m建桥时，桥墩减小了过流面积，输水流量变化较大；在溢流坝上游4、8、12m建桥时，对输水流量的影响逐渐减弱，在溢流坝前12m建桥对溢流坝过流能力的影响最小。

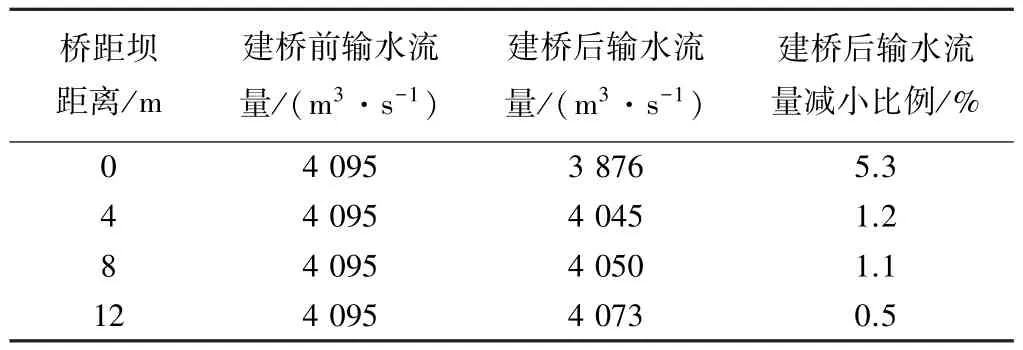
表3 不同桥位下溢流坝过流能力数值模拟结果

6 结 语

鲇鱼山灌区取水枢纽原设计闸墩、底板配筋不能满足现行规范要求，当发生小频率洪水时，易发生回水倒灌，淹没枢纽上游2.6 km处河道右岸地势较低的农田、道路，枢纽建筑物之间缺少检修维护交通桥。除险加固选择对进水闸、冲沙闸进行拆除重建，为解决发生低频率洪水时出现回水倒灌的问题，提出了新建左岸泄洪闸，同时新建检修交通桥。根据鲇鱼山灌区渠首枢纽除险加固的实际情况，对枢纽建筑物输水能力进行了研究。分析表明：虽然建桥后各个建筑物的输水能力都有不同程度的衰减，但衰减率均小于3%，因此仍能满足原规划过流能力要求；在溢流坝前12 m位置建桥对大型灌区枢纽溢流坝的过流能力影响最小。