考虑多因素影响的装配式梁桥横向联系疲劳损伤评估
李岩 杨婷婷 商贺嵩 秦丽辉


摘 要:为探讨实际运营条件下各因素对装配式混凝土梁桥横向联系结构疲劳损伤的影响,基于线性Miner累积损伤准则提出了该类桥型横隔梁钢板连接构造的疲劳评估方法和框架. 依托工程实例,研究了随机交通的动力冲击效应、运行状态和桥面退化等因素对横向联系疲劳损伤的影响规律. 结果表明:相对于按照95%保证率考虑随机车载冲击效应的影响,依照规范给定的冲击系数考虑冲击效应会明显低估构件的实际疲劳寿命;车辆运行状态对疲劳损伤影响显著,其他因素相同情况下,密集运行状态造成的疲劳累积损伤值较一般运行状态时小;桥面退化对横隔梁疲劳损伤影响明显,可造成车辆一般和密集运行状态下的结构疲劳寿命降低60.01%和34.88%. 对新桥横向联系设计,建议考虑规范冲击系数和车辆一般运行状态进行疲劳验算;对既有桥梁疲劳评估,建议按实际交通状况考虑随机车辆冲击效应、车流运行状态和桥面退化的影响.
关键词:疲劳损伤评估;混凝土桥梁;横向联系;车桥耦合振动;桥面退化
中图分类号:U441.3 文献标志码:A
文章编号:1674—2974(2019)09—0079—10
Abstract:To study the effect of actual operational condition on the fatigue damage of lateral connection structure for fabricated concrete girder bridges, a fatigue damage assessment framework for the steel plate connection structure of this bridge type was presented based on linear Miner cumulative damage criterion. The influence rules of dynamic impact effects from stochastic traffic, traffic condition and progressive deterioration of bridge deck roughness on the fatigue damage of lateral connections were studied through an actual bridge example. The results show that the fatigue life of the transversal beam is obviously underestimated when considering the vehicular impact effect under Chinese specification compared with that of stochastic traffic with 95% confidence level. Traffic condition also has a significant influence on the fatigue damage, and the structural fatigue cumulative damage under intensive traffic condition is smaller than that of general one. Progressive deterioration of bridge deck condition has an obvious effect on the fatigue damage. The fatigue life of lateral connection decreased by 60.01% and 34.88% under general and intensive traffic conditions considering bridge deck degradation. When designing a new bridge, the impact factors from specification and general traffic condition should be considered in the fatigue calculation for lateral connection structure. It is suggested that considering the influence of stochastic traffic dynamic impact,operation traffic status and progressive deterioration of bridge deck was necessary when evaluating lateral connection fatigue damage for the existing bridges.
Key words:fatigue damage evaluation;concrete bridges;lateral connection;vehicle-bridge coupled vibration;progressive deterioration of bridge deck
裝配式混凝土肋梁桥通过翼缘板和横隔梁的横向连接使各主梁共同承担车辆荷载作用.有桥梁调查表明[1-2]重载交通的长期反复作用造成的疲劳累积损伤是导致该类桥梁横向联系构件破损和断裂的重要原因,其中又以钢板连接的横向联系损伤问题最为突出[3].横向联系损伤将影响上部结构整体受力性能,严重时可导致“单梁受力”等局部超载现象发生.我国现行桥梁设计规范对此类构件未给出明确的疲劳损伤评估方法及具体防护措施.
目前装配式混凝土梁桥的疲劳问题已得到学者的广泛关注,并开展了大量的研究[4],但对于该类桥梁的横向联系还鲜有关注.有关横向联系疲劳损伤评定的相关研究主要集中在损伤对桥梁整体受力性能的影响方面.姚晓飞等[3]以混凝土梁桥的中横隔梁为研究对象,分析指出若其并未全部破坏,则荷载横向分布系数的变化率随其损伤程度呈现线性规律;刘润阳[5]以简支T梁桥为例对横隔板病害进行研究,指出对其破坏不及时修补将导致主梁破坏;梁志广等[6]对装配式简支T梁的现场检测分析发现,重载车辆导致的横隔梁连接处过大的弯曲应力是造成横隔梁钢板断裂的主要原因.目前关于混凝土梁桥横向联系疲劳损伤的相关研究还鲜有开展,相关影响规律和机理尚不明确.
为此,本文以钢板焊接形式的横向联系为对象,建立基于线性累积损伤准则的装配式肋梁桥横向连接的疲劳评估模型,提出考虑运营车辆动力冲击效应和桥面退化的分析模型.依托某装配式预应力混凝土简支梁桥工程实例,通过数值分析方法获取随机车载及不同运行交通状态下的横向联系热点位置的应力谱.考虑交通量增长和环境因素,进行桥面状况的退化模拟.基于上述理论和方法,开展随机车载动力冲击效应、交通流运行状态和桥面退化等因素对横向联系疲劳损伤的影响研究.
1 典型重车下桥梁冲击效应分析方法
1.1 车桥耦合振动分析原理
采用整体法,通过车桥接触点的作用力和位移的协调關系,建立车桥耦合系统整体运动方程如下:
式中:M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵;Xv和qB分别为车辆和桥梁位移响应向量;F表示车桥系统的荷载向量;符号下标B代表桥梁;符号上下标v代表车辆;符号下标Bv和vB表示车桥耦合项;符号上标r和G分别表示由于桥面不平度和车辆自重产生的作用力.车桥系统振动方程中的质量、刚度、阻尼和荷载向量可由车桥系统间的力和位移协调条件推导得到,具体形式详见文献[7].
对于其中的桥梁动力分析模型,采用模态综合技术建立.利用通用有限元软件建立桥梁计算模型并进行模态分析,提取结构振型和频率等模态信息用于计算车桥动力响应.基于上述原理,笔者采用Matlab开发了专门的车桥耦合振动分析程序,并通过实桥试验验证了程序的准确性和可靠性[7].该程序将用于后继桥例的车桥振动分析.
1.2 典型重车作用下桥梁冲击效应分析
基于全国范围内大量公路交通调查和动态称重数据,及现有研究成果,将当前我国公路中较为常见的重载车型依据车型、轴数和车重等特征归纳为7类典型重车[8-9](如表1所示).
现以2轴重车为例,对车辆计算模型进行简介.模型如图1所示,含12个自由度,下标vr表示车体;s表示悬架;L、R分别表示X轴左侧和右侧刚体.各类车型的空间计算模型运动方程的推导过程和详细参数取值详见文献[9].
采用前述车桥振动分析程序,可开展多种典型重车下桥梁冲击效应分析. 研究表明[10],对于确定的车辆和桥梁,车速和桥面平整度是影响车桥系统动力响应的两类主要因素. 同时,实际运营条件下车辆过桥速度和桥面平整度均具有较大的随机性,导致车辆对桥梁的动力冲击效应也具有较大的离散性.为此,本文针对前述7种典型重车,分别考虑车速和桥面平整度的随机性,进行车辆冲击效应的统计分析,最终得到各类车型和平整度等级下在95%置信水平的横隔梁汽车冲击系数值,并用于后继的结构疲劳评价研究.
2 桥面退化模型
通常利用桥面平整度系数(RRC)和国际平整度指数(IRI)来评价桥面状况,两者的评价方式虽有
所不同,但本质是上相通的,可利用下式进行相互转换[11]:
式中:IRIt为t年运营变化后的国际平整度指数;
φ(n0)为桥面平整度系数;a0为系数,取a0 = 103 m-1.桥面平整度指标通常可划分为5个等级[11].桥面状况会伴随长期的交通荷载和腐蚀作用等影响不断退化. 国际平整度指数随时间变化的公式可表达为[12-13]:
式中:η为环境系数,根据冻结条件与干湿状态一般取0.01~0.7;t为桥梁的运营时间,年;IRI0为桥梁竣工后的初始国际平整度指数;SNC为根据桥面各结构层厚度和强度确定的结构系数[12],对于常规混凝土桥面铺装的桥梁一般可取为4;(CESAL)t为将随时间变化的车流量换算成100 kN的累计当量轴次,以百万次计.
式(2)和式(3)联立,可得桥面平整度系数与时间的关系为:
3 横向联系疲劳寿命评估方法
基于目前各国规范常用的线性疲劳累积损伤准则,建立混凝土梁桥横向联系的钢板连接构造的疲劳寿命评估框架,如图2所示.
3.1 横向连接构件的应力谱计算
横隔梁作为装配式混凝土梁桥各主梁间的连接构件,纵横向影响线长度均较小,其在车载下的动力行为主要受单车控制. 为此,在进行运营交通荷载作用下对横隔梁连接构造的动力分析时,提出如下的简化分析策略(计算流程如图3所示):
1)基于实际交通调查数据,统计分析交通流特征参数,采用Monte-Carlo方法进行随机交通流模拟.
2)根据桥梁图纸和现场实测数据,建立桥梁的空间有限元分析模型.
3)开展典型重车下的车桥耦合振动分析,得到各类重车对应95%保证率的冲击系数.
4)基于拟静力时程分析,获得横向联系构造热点位置的应力影响线.
5)将随机车流中各车辆简化为以车轮为单位
的多个集中力荷载,考虑单车轴距、轮距和多车间距,形成与随机车流荷载等效的集中力荷载队列.
6)根据车型和其他影响因素考虑动力冲击效
应,并进行随机车流下的影响线加载,获得典型日钢板连接构造热点位置应力时程,经雨流法处理后得到应力谱.
根据上述原理,作者采用Matlab编制了随机车流过桥的影响线加载程序[9].
3.2 横隔梁钢板连接的疲劳寿命评估
基于线性Miner准则,荷载循环加载次数(疲劳寿命)与构件应力幅(疲劳荷载效应)关系为:
式中:Nf 疲劳破坏时构件经历的应力循环次数;Δσ构件承受的应力幅;C为疲劳细节常数,m为与材料特性相关的常数,本研究依据我国现行钢结构桥梁设计规范选取,具体取值与构造细节有关,将依托后继的实例给出[14].
依据疲劳损伤等效原理,可得变幅应力作用对应的疲劳等效应力幅为:
式中:Δσeq为等效应力幅;ni为应力幅Δσi对应的循环次数;∑ni为等效应力幅的应力循环总数.
综上所述,变幅应力循环引起的疲劳累积损伤为:
式中:D为累积损伤指数;Ni为第i级应力幅Δσi下构件的疲劳寿命;Di为第i级应力幅Δσi下构件发生的疲劳损伤累计值.当累积疲劳损伤值超过临界损伤时,构件疲劳失效.一般将Dcr = 1作为疲劳破坏临界值.
基于前述简化分析可得到典型日交通荷载下疲劳热点位置的应力时程,采用雨流计数法进行应力幅统计. 通过式(5)將得到的随机变幅应力循环换算成等效应力幅Δσeq,则典型日交通荷载下热点位置的疲劳累积损伤可表达为:
式中:Dd为热点位置典型日的疲劳损伤累积值;Nd为桥梁构件典型日内承受的变幅应力循环总次数;Nc为等效应力幅对应疲劳寿命.构件疲劳寿命Ty为:
式中:Ty为结构疲劳寿命估计值,单位为年;Dy为预期疲劳荷载下结构1年内的疲劳累积损伤值.
4 工程实例
4.1 桥梁计算模型与疲劳热点位置
以一座跨铁路立交桥为例开展后续的分析研究. 该桥位于市区电厂、钢厂等工业集中区域连接外部公路的通道位置,特殊的区域环境造成该桥过桥交通流具有重载车辆占比高,且特定车型集中的特点.本文选取其中30 m跨径装配式预应力混凝土简支梁桥开展分析研究(横断面如图4所示).该跨含5道内横隔梁,2道端横隔梁,横向联系采用预埋钢板焊接连接构造形式(如图5所示).
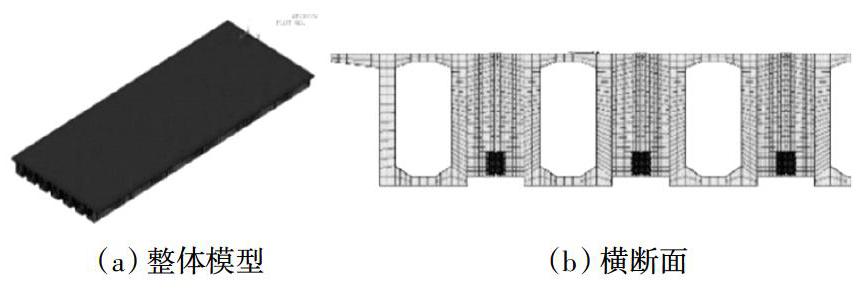
通过ANSYS建立该桥上部结构的有限元模型(如图6所示),其中主梁和横隔梁采用Solid65实体单元模拟,分别划分为约10 cm×5 cm×5 cm和5 cm×5 cm×5 cm的六面体单元,两尺寸单元间采用共用节点连接(如图6(b));横隔梁预埋主筋采用Link8杆单元模拟,并与混凝土实体单元以共用节点形式连接;梁内预埋钢筋与预埋钢板的焊接连接采用建立约束方式方法模拟;预埋钢板与横隔梁间的连接采用自动生成约束方程[15]方式模拟;预埋钢板与盖板采用壳单元模拟,单元尺度为1 cm,焊接采用节点耦合方式模拟;支座模拟直接采用约束梁底节点的方式.
采用表1中M1双轴重车在不同车道过桥工况的静力分析,得到车载下跨中截面横隔梁受力最为不利,最大正应力31.7 MPa和剪应力12.2 MPa发生在横隔梁下缘焊接连接钢板的不同位置.根据我国现行公路钢结构桥梁设计规范,确定了本桥例钢板连接疲劳细节类别为“45*”,进而得到正应力和剪应力S-N曲线[14].
正应力:lg N = 11.260 7 - 3lg Δσ(N < 5 × 106)
剪应力:lg N = 15.816 5 - 5lg Δσ(N ≤ 108)
通过对上述两处热点位置进行多种典型重车不利组合作用下的应力分析,发现其剪应力最大应力幅均低于规范给定的疲劳强度限值,可不进行疲劳验算,具体过程详见文献[9]. 故本文横隔梁钢板连接疲劳评估中忽略剪应力的影响,仅考虑正应力的影响.后继的横向联系钢板连接疲劳评估以最大正应力处为疲劳热点位置进行.
4.2 运营交通模拟
研究表明,运营交通荷载的主要特征参数包括车辆类型、车重和车辆间距都服从一定的随机分布,并在任一时刻其出现的组合可视为一个随机出过程[8].对桥例所在地进行为期两周(2013年5月15日至28日)的交通量统计数据,得到过桥货车共计68 040辆,客货比约为3 ∶ 7,日均交通量为6 943辆,重车数据如表2所示.
通过对车辆特征参数运用K-S检验法进行随机分布的优度拟合,并对车辆荷载的各随机变量参数运用极大似然法进行估计,确定随机车辆荷载各特征参数符合的随机分布类型及参数.现以日交通量6 943辆(货车4 860辆)作为模拟样本容量,并对随机车辆荷载运用Monte-Carlo法进行模拟,得到一般运行状态[8,16]下随机车流样本模拟结果,如图7所示,其中竖坐标为模拟车重,车道一和二为分别表示双向外侧车道,横坐标为车流中车辆位置. 详细模拟过程和相关参数见文献[9].
4.3 典型重车对钢板连接构造的冲击效应分析
本研究考虑“好”、“一般”和“差”三类桥面平整度状况,7种重车车型(M1~M7)和9种车速(20~100 km/h,间距10 km/h)的组合工况189种(各工况含10个不平度样本),共进行1 890个样本的车桥动力分析.基于分析结果,对多车速和平整度样本的横隔梁钢板连接构造疲劳热点位置的车载动力冲击效应进行统计分析,并采用应力冲击系数表征车辆动力冲击效应引起热点位置应力响应相对静力作用对应应力响应的放大程度,利用K-S法对结果进行检验,发现确定车型和桥面平整度等级的应力冲击系数服从正态分布,相关分析过程详见文献[7].
2)橫向联系疲劳评估中,相对于按照95%保证率考虑随机车载冲击效应的影响,依照规范给定的冲击系数考虑冲击效应会明显低估构件的实际疲劳寿命.
3)桥面退化对横向联系疲劳损伤具有明显影响;一般与密集运行状态下考虑桥面退化时横向联系的疲劳寿命较不计桥面退化对应的疲劳寿命分别降低了60.01%和34.88%.
4)横向联系设计中建议偏安全地按规范给定冲击系数和一般运行状态进行疲劳验算;既有结构疲劳评估时,建议按实际交通状况考虑随机车辆冲击效应、车流运行状态和桥面退化的影响,以保证评估结果的可靠性.
参考文献
[1] DENG L,WANG W,YU Y. State-of-the-art review on the causes and mechanisms of bridge collapse [J]. Journal of Performance of Constructed Facilities,2016,30(2):04015005-1—04015005-13.
[2] 郑彬双. 横隔板对钢筋混凝土肋梁桥疲劳性能的影响分析[D]. 哈尔滨:东北林业大学土木工程学院,2017:1—3.
ZHENG B S. Analysis of diaphragms influence on the fatigue properties of reinforced concrete rib beam bridge [D]. Harbin:School of Civil Engineering,Northeast Forestry University,2017:1—3. (In Chinese)
[3] 姚晓飞,徐岳,丁怡洁,等. 翼缘刚接混凝土T梁桥结构体系损伤评价研究[J].武汉理工大学学报,2010,32(1):169—173.
YAO X F,XU Y,DING Y J,et al. Research on damage assessment of rigid-jointed concrete T-beam bridge system [J]. Journal of Wuhan University of Technology,2010,32(1):169—173. (In Chinese)
[4] 杨鸥,张晓非,霍静思,等.预应力混凝土梁疲劳性能研究现状[J]. 建筑科学与工程学报,2017,34(4):85—95.
YANG O,ZHANG X F,HUO J S,et al. Research status of fatigue performance of pre-stressed concrete beam [J]. Journal of Architecture and Civil Engineering,2017,34(4):85—95.(In Chinese)
[5] 刘润阳. T梁横隔板不同连接状态对主梁受力的影响[J].铁道建筑,2009(3):46—48.
LIU R Y. Influence of different connection state of T-beam diaphragm on main girder stress [J]. Railway Engineering,2009(3):46—48. (In Chinese)
[6] 梁志广,张勇,刘建磊. 装配式T梁横隔板病害及加固[J].中国市政工程,2007(5):92—93.
LIANG Z G,ZHANG Y,LIU J L. Disease and reinforcement of the assembly type T-beam diaphragm [J]. China Municipal Engineering,2007(5):92—93. (In Chinese)
[7] LI Y,CAI C S,LIU Y,et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches [J]. Engineering Structures,2016,106(1):243—260.
[8] 张喜刚. 公路桥梁汽车荷载标准研究[M]. 北京:人民交通出版社,2014:206—209.
ZHANG X G. Study on vehicle load standard for highway bridge[M]. Beijing:China Communications Press,2014:206—209. (In Chinese)
[9] 商贺嵩. 装配式混凝土梁桥横向联系的疲劳评定研究[D].哈尔滨:哈尔滨工业大学交通科学与工程学院,2017:42—45.
SHANG H S. Fatigue assessment for the transversal connection of assembled concrete beam bridge [D]. Harbin:School of Transportation Science and Engineering,Harbin Institute of Technology,2017:42—45. (In Chinese)
[10] 韓万水,闫君媛,武隽,等.基于长期监测的特重车流作用下桥梁动态放大系数研究[J].振动工程学报,2014,27(2):222—232.
HAN W S,YAN J Y,WU J,et al. Analysis of bridge dynamic amplification factors under extra-heavy truck scenarios based on long-term monitoring data [J]. Journal of Vibration Engineering,2014,27(2):222—232.(In Chinese)
[11] 殷新锋,丰锦铭,刘扬,等. 基于桥面退化模型的在役桥梁冲击系数研究[J]. 应用力学学报,2016,33(3):516—523.
YIN X F,FENG J M,LIU Y,et al. Analysis of impact factor on the bridges in service based on the progressive deterioration model of road surface [J]. Chinese Journal of Applied Mechnaics,2016,33(3):516—523. (In Chinese)
[12] ZHANG W,CAI C S. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions [J]. Journal of Bridge Engineering,2012,17(3):443—453.
[13] 殷新锋,丰锦铭,刘扬,等. 考虑车-桥耦合振动及桥面平整度退化影响的拱桥吊杆疲劳分析[J]. 湖南大学学报(自然科学版),2017,44(9):17—25.
YIN X F,FENG J M,LIU Y.et al. Fatigue analysis for suspenders of arch bridge addressing vehicle-bridge coupled vibration and road surf ace progressive deterioration [J]. Journal of Hunan University (Natural Sciences),2017,44(9):17—25. (In Chinese)
[14] JTGD 64—2015 公路钢结构桥梁设计规范[S]. 北京:人民交通出版社,2015:28—32.
JTGD 64—2015 Specification for design of highway steel bridge [S]. Beijing:China Communications Press,2015:28—32. (In Chinese)
[15] 谢元丕,冯刚. ANSYS三维实体单元与板壳单元的组合建模研究[J]. 机械设计,2009,26(4):5—7.
XIE Y P,FENG G. Study of ANSYS modelling on the combination of 3D entity unit and plate-shell unit [J]. Journal of Machine Design,2009,26(4):5—7.(In Chinese)
[16] 李扬海. 公路桥梁结构可靠度与概率极限状态设计[M]. 北京:人民交通出版社,1997:140—156.
LI Y H. The reliability calculation and probabilistic limit state design of highway bridge structure[M]. Beijing:China Communications Press,1997:140—156.(In Chinese)

