轻钢组合楼盖面内刚度和承载力计算方法研究

管宇 周绪红 石宇 姚欣梅

摘   要：为研究冷弯薄壁型钢组合楼盖的面内刚度和承载能力，采用ABAQUS软件建立楼盖有限元模型，通过轻钢楼盖面内滞回试验结果进行验证.研究不同参数对楼盖模型面内刚度和承载力的影响规律，结果表明：改变楼盖梁尺寸、楼盖梁腹板开孔面积和间距以及扁钢带和刚性支撑件的布置方式对楼盖面内刚度和承载力影响较小，减小自攻螺钉连接间距和组合楼盖的长宽比能提高组合楼盖的面内刚度和承载力，在20～40 mm范围内改变楼板厚度对组合楼盖面内刚度和承载力存在一定影响.基于组合楼盖的破坏模式和受力机理，楼盖的面内极限承载力可通过单颗自攻螺钉连接的承载力和楼盖两侧自攻螺钉连接的数量进行估算.基于退化四折线模型，建立组合楼盖面内刚度的计算方法，为轻钢楼盖的工程设计与应用提供理论依据.

关键词：冷弯薄壁型钢;楼盖;刚度和承载力;计算方法;刚性楼盖

中图分类号：TU392.5;TU398                  文献标志码：A

文章编号：1674—2974（2019）09—0031—13

Abstract： In order to investigate the in-plane stiffness and bearing capacity of cold-formed thin-walled steel composite floor， a floor model was established through ABAQUS software and verified by the in-plane cyclic loading test results. Further， the effect of different parameters on the in-plane stiffness and bearing capacity of the floor model was studied. The results showed that the influence of the joist size，the opening area and spacing of joist web， flat strap and blocking layout on the in-plane stiffness and bearing capacity of composite floors was insignificant. The in-plane stiffness and bearing capacity of composite floors can be improved by decreasing the screw spacing and the length-to-width ratio of floor. The change of slab thickness in the range of 20～40 mm had a certain effect on the in-plane stiffness and bearing capacity of composite floors. Based on the failure modes and mechanical behavior of composite floors， the ultimate bearing capacity of floor can be estimated by the load-carrying capacity of the single self-tapping screw and the number of self-tapping screws connected on both sides of floor. The calculation method for in-plane stiffness of composite floors was established based on the degenerate quadri-polyline model， which provided a theoretical basis for engineering design and application of thin-walled steel floors.

Key words：cold-formed thin-walled steel;floors;stiffness and load-carrying capacity;calculation method;rigid floor

組合楼盖是冷弯薄壁型钢结构房屋中的水平结构构件和抗剪墙体的水平支撑，起着承担荷载和分配荷载的重要作用.在工程应用中，组合楼盖必须具备良好的面内刚度和承载能力.

国内外学者对楼盖的面内受力性能进行了大量的试验研究.Countryman等[1-2]和Bott[3]对胶合覆面板木楼盖足尺试件进行了单调加载试验，研究表明木楼盖的面内受力机理类似于宽翼缘的工字梁，且楼盖面内变形以剪切变形为主，楼盖的面内刚度和承载力取决于楼面搁栅与覆面板间钢钉连接的尺寸和间距. Tissell等[4]通过木楼盖面内加载试验研究，表明覆面板类型和材料级别对楼盖面内刚度和承载力影响较小，楼盖梁采用薄壁型钢比采用木搁栅具有更好的面内刚度，增加钢钉数量和覆面板厚度能有效提高楼盖的面内承载力. Nikolaidou等[5]和Chatterjee等[6]对冷弯薄壁型钢-OSB板组合楼盖的面内受力性能进行了滞回试验研究，指出组合楼盖面内破坏主要与楼盖周边的螺钉连接失效有关，基于螺钉连接滑移曲线建立了楼盖面内位移的计算公式. Loss等[7]和马仲等[8]对新型钢-木混合楼盖进行了面内往复加载试验，指出楼盖面内变形以剪切变形为主，楼盖破坏特征为面板钉剪断，螺钉连接的受力性能是影响楼盖面内刚度和承载力的主要因素.管宇等[9]和石宇等[10]对冷弯薄壁型钢-石膏基自流平砂浆组合楼盖进行了面内滞回试验研究，指出组合楼盖面内破坏模式为两侧楼盖梁与压型钢板间自攻螺钉倾斜、被拔出和剪断，采用钢丝网抗剪构造可提高楼盖的面内刚度，但对楼盖的面内承载力存在不利影响.

本文基于冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的试验研究[10]，采用ABAQUS软件对不同参数组合楼盖模型面内刚度和承载力的变化规律进行分析，提出冷弯薄壁型钢组合楼盖面内极限承载力和面内刚度的计算方法，为完善冷弯薄壁型钢结构的理论体系和设计方法提供参考依据，以指导工程设计.

1   有限元分析结果验证

1.1   有限元模型建立

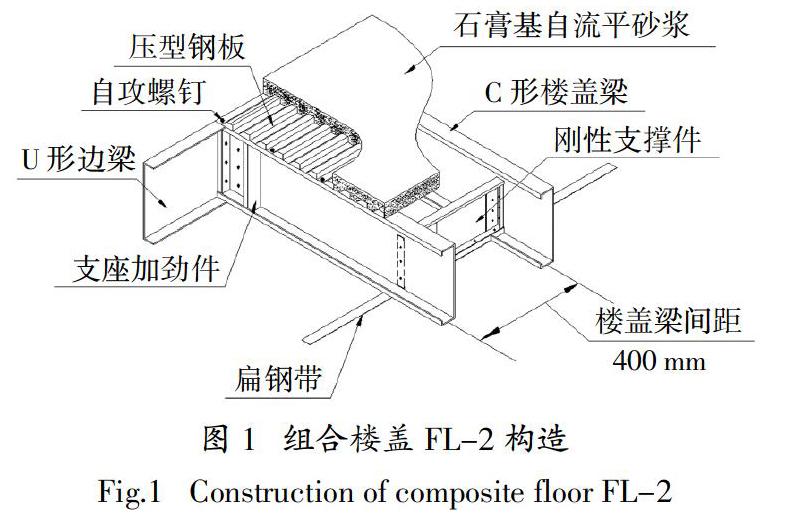
参照文献[10]冷弯薄壁型钢-石膏基自流平砂浆组合楼盖试件FL-2的面内加载试验，试件尺寸为3.6 m × 3.6 m，楼盖梁规格为C254×40×13×1.5 mm，间距为400 mm，梁端加劲件采用C100×35×12×1.5 mm，U形边梁规格为U254×40×1.5 mm，楼盖梁之间采用ST4.8自攻螺钉进行连接.在边部和中部楼盖梁之间设置3个规格为C200×40×14×1.5 mm的刚性支撑件，并在楼盖梁跨中设置宽度为50 mm，厚为1 mm的扁钢带拉条. 楼面板采用在0.75 mm厚热镀锌钢板YX-14-63-820 mm压型钢板上浇筑40 mm厚C30石膏基自流平砂浆，楼面板未设置抗剪构造措施，压型钢板与楼盖梁之间采用ST5.5自攻螺钉进行连接，组合楼盖构造示意图见图1.

建立组合楼盖FL-2有限元模型，见图2. 模型中楼盖梁、压型钢板、加劲件、刚性支撑件、扁钢带等冷弯薄壁型钢构件均采用壳单元S4R来模拟，其中楼盖梁的网格尺寸为100 mm，加劲件、刚性支撑件和扁钢带的网格尺寸为50 mm，压型钢板的网格尺寸为200 mm. 石膏基自流平砂浆面板采用实体单元C3D8R来模拟，网格尺寸为200 mm. 采用Radial-Thrust连接单元来模拟自攻螺钉连接，输入的荷载-位移关系参照文献[11]中自攻螺钉推出试验结果.在组成楼盖的基本构件间建立摩擦接触，切向采用库仑摩擦，抗滑移系数为0.3，法向采用硬接触. 采用黏结单元COH3D8在石膏基自流平砂浆与压型钢板之间建立0.5 mm厚的黏结层以模拟界面剂的受力行为，定义Traction-Separation双线性本构关系[12].

冷弯薄壁型钢采用Von Mises屈服准则、随动强化准则和关联流动法则以正确模拟材料的包辛格效应. 钢材的本构模型为双折线，楼盖梁的屈服强度fy为318.4 MPa，抗拉强度fu为369.6 MPa，弹性模量为2.09×105 MPa;压型钢板的屈服强度fy为356.3 MPa，抗拉强度fu为438.6 MPa，弹性模量为2.00×105 MPa，钢材的泊松比为0.3.石膏基自流平砂浆的本构关系参考混凝土的塑性损伤模型进行设置，输入参数详见文献[13].

在全局坐标系的Y方向输入重力加速度g = 9.8 m/s2以考虑楼盖自重.采用耦合约束将组合楼盖加载点范围内的所有节点设置为一个参考点，施加沿Z向的循环往复位移，屈服前每级循环一次，屈服后每级循环3次.约束两侧楼盖梁固定区域所有节点的6个自由度模拟试验的边界条件.

1.2   有限元模型验证

组合楼盖FL-2破坏现象有限元与试验对比见图3，滞回曲线和骨架曲线有限元与试验对比见图4，骨架曲线特征点有限元与试验对比见表1.

由图3可知，楼盖模型的典型破坏特征与试验现象吻合较好，表现为组合楼板在固定边位置处发生黏结破坏（图3（a）），压型钢板屈曲变形及加载点处楼盖梁局部屈曲（图3（b）），组合楼板与楼盖梁发生滑移现象（图3（c）），固定边梁与压型钢板之间自攻螺钉连接破坏（图3（d）），最后试件破坏. 由图4可知，组合楼盖经历了弹性阶段、弹塑性阶段和破坏阶段. 在弹性阶段，楼盖的塑性变形能力较强，具备较强的耗能性能;进入弹塑性阶段后，楼盖的滞回曲线因压型钢板的局部屈曲、砂浆面板的裂缝在循环作用下的张合现象以及螺钉连接失效而发生捏缩效应，并出现强度和刚度退化现象;进入破坏阶段后，楼盖表现出明显的强度和刚度退化，耗能能力逐步降低.滞回曲线有限元分析结果能反映出冷弯薄壁型钢组合楼盖强度和刚度的发展过程和变化规律.

由表1可知，组合楼盖在循环加载过程中，因连接反向加载梁的螺栓发生松动，加载铰支座与发生屈曲变形的U形楼盖梁接触不紧密，影响了反向荷载的施加，楼盖出现了拉压不均的受力现象，导致反向有限元分析结果与试验结果出现较大偏差. 除此之外，有限元模型的弹性刚度及各阶段特征点的分析结果与试验结果的误差均小于15%，表明有限元模型可用来模拟组合楼盖在水平往复荷载作用下面内的受力性能，建模方法正确.

2   有限元变参数分析

为深入研究冷弯薄壁型钢组合楼盖面内的受力性能，在试验楼盖模型的基础上，改变钢材属性，其屈服強度fy为345 MPa，弹性模量为2.06×105 MPa.将试验的4点加载方式改为均布加载，变参数分析模型均采用单调加载的方式来研究楼盖面内的受力性能.

2.1   螺钉间距的影响

在楼盖模型中改变楼盖梁与压型钢板间螺钉连接间距，分别取压型钢板波距的2倍、4倍和8倍，即125 mm、250 mm和500 mm.有限元模型弹性刚度及各阶段承载力和位移见表2.螺钉间距对组合楼盖弹性刚度和极限荷载的影响曲线见图5.

由图5、表2可知：1）当周边螺钉间距为125 mm，中间螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低1.9%和7.6%，极限荷载依次降低0.3%和1.3%;当中间螺钉间距为125 mm，周边螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低52.3%和48.3%，极限荷载均降低44.7%.当周边螺钉间距为250 mm，中间螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低2.9%和13.6%，极限荷载依次降低0.7%和0.2%;当中间螺钉间距为250 mm，周边螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低52.8%和49.9%，极限荷载依次降低44.9%和44.5%.当周边螺钉间距为500 mm，中间螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低5.8%和17.7%，极限荷载依次降低0.2%和0.6%;当中间螺钉间距为500 mm，周边螺钉间距依次从125 mm增至500 mm时，楼盖的弹性刚度依次降低55.8%和52.3%，极限荷载依次降低44.3%和44.7%.2）自攻螺钉间距是影响组合楼盖面内受力性能的重要因素.对于周边螺钉间距相同的模型，改变中间螺钉间距对楼盖面内刚度和各阶段承载力和位移影响较小;而对于中间螺钉间距相同的模型，改变周边螺钉间距对楼盖面内刚度和各阶段承载力和位移影响较大. 3）减小自攻螺钉间距可有效提高组合楼盖的面内受力性能.

在工程设计中，参照压型钢板的规格和文献[14]中螺钉间距的规定，建议周边螺钉间距取为压型钢板单波距的倍数和150 mm的最小值，中间螺钉间距取为周边螺钉间距的2倍.

2.2   楼板厚度的影响

在楼盖模型中改变楼盖面板的厚度，选取樓板厚度从20 mm至80 mm.有限元模型弹性刚度及各阶段承载力和位移见表3.楼板厚度对组合楼盖弹性刚度和极限荷载的影响曲线见图6.

由图6、表3可知：1）当楼板厚度由20 mm增至80 mm时，组合楼盖面内的弹性刚度依次增大13.4%、12.7%、0.8%、0.2%、1.7%和1.8%，极限荷载依次增大1.9%、2.2%、0.2%、0.1%、0.2%和0.2%.2）改变楼板厚度对组合楼盖面内的受力性能存在一定影响.当楼板厚度处于20～40 mm，改变楼板厚度对楼盖面内受力性能影响较大，近似于线性变化;当楼板厚度处于50～80 mm，改变楼板厚度对楼盖面内受力性能的影响较小.

在工程设计中，参照文献[14]中楼面板厚度的规定，建议楼面板厚度选取40 mm，这样既可减轻楼盖的自重又不降低楼盖面内的受力性能，能达到最好的经济效益.

2.3   楼盖梁尺寸及布置间距的影响

在楼盖模型中改变楼盖梁截面尺寸和楼盖梁间距，其中楼盖梁规格选用C205×40×14×1.5 mm+U205×40×1.5 mm、C255×40×14×1.5 mm+U255×40×1.5 mm和C305×40×14×1.5 mm+U305×40×1.5 mm共3类，C形楼盖梁间距选用400 mm和600 mm.有限元模型弹性刚度及各阶段承载力和位移见表4.楼盖梁尺寸对楼盖弹性刚度和极限荷载的影响曲线见图7.

由图7、表4可知：1）对于梁间距为400 mm的模型，随着楼盖梁尺寸的增加，楼盖面内的弹性刚度依次增大3.3%和3.1%，极限荷载依次增大0.5%和降低0.1%.对于梁间距为600 mm的模型，随着楼盖梁尺寸的增加，楼盖面内的弹性刚度依次增大6%和1.4%，极限荷载依次增大0.7%和降低0.2%.故改变楼盖梁的尺寸对组合楼盖面内的受力性能影响较小.2）对于C205截面模型，当梁间距由400 mm变为600 mm时，楼盖面内的弹性刚度降低31.5%，极限荷载降低0.6%;对于C255截面模型，当梁间距由400 mm变为600 mm时，楼盖面内的弹性刚度降低29.7%，极限荷载降低0.4%;对于C305截面模型，当梁间距由400 mm变为600 mm时，楼盖面内的弹性刚度降低30.9%，极限荷载降低0.5%.故改变楼盖梁间距对楼盖面内弹性刚度影响较大，而对面内承载能力影响较小.

在工程设计中，应根据房屋建筑开间尺寸及使用要求，确定楼盖梁的尺寸及布置间距，并需要验算压型钢板-石膏基自流平砂浆楼板与楼盖梁构成的组合梁在施工阶段和使用阶段的强度和挠度.为了提高组合楼盖的竖向承载能力、抗弯刚度以及面内刚度，应避免楼盖梁的间距过大，建议选取楼盖梁的间距为400 mm.

2.4   楼盖梁开孔面积的影响

为降低层高而让管线从楼盖梁中通过，需在楼盖梁上开设孔洞.建立楼盖梁不同开孔面积的有限元模型，见图8，图中孔径R分别选用30～100 mm共8个模型.有限元模型弹性刚度及各阶段承载力和位移见表5.楼盖梁开孔面积对组合楼盖弹性刚度和极限荷载的影响曲线见图9.

由图9、表5可知：1）模型C30～C100（开设孔洞）与模型C0（未设孔洞）相比，楼盖面内的弹性刚度降低约3.7%，极限荷载降低约0.7%.故在楼盖梁开设孔洞对组合楼盖的面内受力性能影响较小. 2）从30～100 mm依次增大孔洞半径，楼盖模型面内的弹性刚度和极限荷载变化幅度均小于1%. 故改变楼盖梁开孔面积对组合楼盖面内的受力性能影响较小.

2.5   楼盖梁开孔间距的影响

在楼盖模型中改变楼盖梁的开孔间距，见图10，图中开孔间距e分别选用300～1 200 mm共6个楼盖模型.有限元模型弹性刚度及各阶段承载力和位移见表6.楼盖梁开孔间距对组合楼盖弹性刚度和极限荷载的影响曲线见图11.

由图11、表6可知：从300 ～1 200 mm依次增大孔洞间距，楼盖模型面内的弹性刚度依次增加3.9%、0%、1.5%、2.7%和0.7%，极限荷载的变化幅度均小于0.5%.故改变楼盖梁孔洞间距对组合楼盖面内的受力性能影响较小.

在工程设计中，参照文献[14]对楼盖梁腹板开孔的规定，建议孔洞面积和孔洞间距可按照水电管线的布置方式进行设计，但需要验算孔洞削弱对楼盖梁受弯强度的影响.不满足强度要求时，可采用钢板或槽型冷弯薄壁型钢构件对孔洞进行加强.

2.6   楼盖长宽比的影响

在楼盖模型宽度不变的基础上，改变模型的长度，分别选取1.8～10.8 m共5个楼盖模型，模型长宽比λ分别为0.5～3.有限元模型弹性刚度及各阶段承载力和位移见表7.楼盖长宽比对组合楼盖弹性刚度和极限荷载的影响曲线见图12.

由图12、表7可知：1）当楼盖长宽比由0.5增至3时，楼盖面内的弹性刚度依次降低3.6%、14.3%、16.2%和17.1%.故当楼盖长宽比小于1时，增大楼盖的长宽比对楼盖面内刚度的影响较小，而当楼盖长宽比大于1时，增大楼盖的长宽比会显著降低楼盖的面内刚度.2）当楼盖长宽比由0.5增至3时，楼盖面内的极限承载力依次降低2.8%、0.1%、0.1%和3.9%.故当楼盖长宽比在1～2之间时，对楼盖面内承载能力影响较小，而当楼盖长宽比大于2时，增大楼盖的长宽比会降低组合楼盖的面内承载力. 3）增大楼盖长宽比会降低组合楼盖的面内受力性能.

在工程设计中，参照文献[15]中对抗震墙之间楼盖长宽比的规定，建议冷弯薄壁型钢组合楼盖的长宽比不应大于3，若不满足要求，可采用钢板或槽型冷弯薄壁型钢构件对U形边梁的端部进行加固处理.

2.7   楼盖支撑系统布置方式的影响

在楼盖模型中改变刚性支撑件和扁钢带的布置方式，其中刚性支撑件选取中间和边跨布置、间隔布置及满跨布置3种方式，扁钢带选取中间设置1道和三分点处设置1道2种方式.有限元模型弹性刚度及各阶段承载力和位移见表8.扁钢带布置方式对组合楼盖弹性刚度和极限荷载的影响曲线见图13. 刚性支撑件布置方式对组合楼盖弹性刚度和极限荷载的影响曲线见图14.

由图13、图14、表8可知：1）模型SP1相比于模型SP0，面内弹性刚度增大3.9%，极限荷载增大0.9%;模型SP2相比于模型SP1，面内弹性刚度增大1.5%，面内极限荷载增大0.2%.故扁钢带布置方式对组合楼盖的面内受力性能影响较小. 2）对于模型SP1-A、SP1-B和SP1-C，增加刚性支撑件的数量，楼盖面内的弹性刚度分别提高了0.5%和1.8%，极限荷载分别降低了0.3%和提高了0.6%;对于模型SP2-A、SP2-B和SP2-C，增加刚性支撑件的数量，楼盖面内的弹性刚度分别提高了0.2%和1.3%，极限荷载分别提高了0.1%和0.0%.故刚性支撑件布置方式对组合楼盖的面内受力性能影响较小.

在工程设计中，参照文献[14]对楼盖支撑系统的布置要求，当楼盖跨度大于3.6 m时，建议在楼盖梁跨中位置布置1道扁钢带，并在扁钢带两端设置刚性支撑件.

3   组合楼盖面内极限承载力计算方法

冷弯薄壁型钢组合楼盖的面内受力机理如同宽翼缘的深梁，见图15. 抗剪墙体等效为深梁的端部支撑，以承担楼盖传递的水平荷载;楼板等效为

深梁的腹板，以抵抗楼盖面内的水平剪力;楼盖边梁等效为深梁的翼缘，以抵抗由弯曲产生的拉、压力.组合楼盖的面内荷载是通过楼盖梁与楼板之间的自攻螺钉连接进行传递的，由楼盖中部向楼盖两侧传递，形成累积现象，致使楼盖两侧螺钉连接承担的面内荷载大于楼盖中间螺钉连接.

由文献[10]试验现象可知，组合楼盖因两侧C形楼盖梁与压型钢板间的自攻螺钉连接发生倾斜、拔出或剪断，导致组合楼盖的面内承载力降低，最终破坏.在加载过程中，楼盖U形边梁和中间C形楼盖梁与压型钢板间的自攻螺钉连接始终处于正常工作状态，并未发生破坏. 试验破坏特征与组合楼盖的受力机理相吻合，故组合楼盖的面内极限承载力可通过单颗自攻螺钉连接的承载力和楼盖两侧自攻螺钉连接的数量進行估算，如公式（1）：

式中：Pmax为组合楼盖面内极限承载力;B为楼盖的宽度;s为楼盖两侧自攻螺钉连接的间距;Ps为单颗自攻螺钉连接的极限承载力，参照文献[11]的试验结果确定.

文献[10]组合楼盖面内极限承载力试验结果与公式（1）计算结果对比见表9. 由表可知，采用公式（1）可合理估算组合楼盖的面内极限承载力，试验结果与公式计算结果产生误差的原因为：由公式计算得到的自攻螺钉个数小于试验实际设置的自攻螺钉个数，如试验时楼盖试件在压型钢板搭接位置会连续设置自攻螺钉.

4   组合楼盖面内刚度计算方法

采用退化四折线模型[16]分析组合楼盖的骨架曲线，见图16.

该模型分4个阶段：1）弹性阶段，临界荷载取为Pe = 0.4Pmax，弹性位移为Δe，弹性刚度为K1;2）屈服前阶段，屈服荷载为Py，屈服位移为Δy，屈服刚度为K2;3）屈服后阶段，极限荷载为Pmax，极限位移为Δmax，极限刚度为K3;4）破坏阶段，破坏荷载为Pu = 0.85Pmax，破坏位移为Δu，破坏刚度为K4. 前3个阶段面内刚度计算方法如公式（2）：

式中：绝对值内+表示正向加载;绝对值内-表示反向加载;Δe、Δy和Δmax按照文献[12]建议的冷弯薄壁型钢组合楼盖面内位移计算公式计算得到.

通过公式（2）计算得到文献[10]中组合楼盖面内弹性刚度K1、屈服刚度K2和极限刚度K3的理论结果与试验分析结果见表10. 由表10可知，采用组合楼盖面内刚度公式（2）得到的楼盖面内刚度计算结果与试验结果相近，误差大体小于15%，主要原因为在试验加载中连接杆螺栓松动导致楼盖面内承载力降低，同时影响了反向加载时楼盖位移的测取结果，最终对组合楼盖面内刚度的试验结果产生影响.

5   组合楼盖面内刚度判定

研究组合楼盖的平面内刚度可确定水平荷载通过楼盖传递至剪力墙的分配关系.采用ABAQUS软件建立3层2跨的组合结构，见图17所示，层高为3 m，宽度为3.6 m，长度为7.2 m.墙架柱采用间距为400 mm的C140×41×14×l.6 mm截面，端柱采用双肢2C140×41×14×l.6 mm的背靠背截面，U形导轨的规格为U141×34×l.6 mm，墙面板采用12 mm的OSB板，墙体采用ST4.8型自攻螺钉进行连接，各层组合墙体抗侧刚度的比值为1 ∶ 1 ∶ 1.组合楼盖规格同1.1节楼盖模型，楼盖梁为间距400 mm的C254×40×13×1.5 mm截面，边梁为U254×40×1.5 mm截面，楼板采用在0.75 mm厚YX-14-63-820压型钢板上浇筑厚度为40 mm的C30石膏基自流平砂浆，楼盖采用ST5.5型自攻螺钉进行连接.组合楼盖和组合墙体的连接方式参照文献[14]中楼盖和墙体的构造要求.建模方法同1.1节，约束底层墙体底导轨所有节点的6个自由度以模拟固端约束的边界条件.对各层组合楼盖最外侧区域所有节点施加Z向的均布荷载以模拟水平荷载作用，如图17所示.

参照文献[15]计算8度抗震设防烈度，0.2g设计基本地震加速度值作用下，各楼层水平地震作用设计值见表11，各层组合墙体承担水平剪力有限元结果见表11. 由有限元分析结果和表11可知，模型各层水平荷载通过组合楼盖分配至组合墙体的分配关系相同，比值关系为1 ∶ 1 ∶ 1，3片组合墙体承担水平剪力的比值与自身抗侧刚度的比值相同，表明水平荷载在组合墙体之间的分配关系是按照墙体自身刚度的比值进行分配的. 同一楼层的组合楼盖各位置处变形相近，各层组合楼盖表现为刚体运动.综上可知，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖为刚性楼盖.

6   结   论

通过对冷弯薄壁型钢组合楼盖进行有限元参数分析和计算理论研究，得到以下结论：

1）减小自攻螺钉间距和楼盖长宽比可有效提

高组合楼盖的面内刚度和承载力，而改变楼盖梁尺寸、楼盖梁开孔面积和间距以及楼盖支撑系统布置方式对组合楼盖面内的受力性能影响较小.当楼板厚度处于20 ～ 40 mm，改变楼板厚度对楼盖面内受力性能影响较大;当楼板厚度处于50 ～ 80 mm，改变楼板厚度对楼盖面内受力性能的影响较小.

2）组合楼盖的面内荷载是通过楼盖梁与楼板

之间的自攻螺钉连接进行传递的，由楼盖中部向楼盖两侧传递.组合楼盖的面内极限承载力可通过单颗自攻螺钉连接的承载力和楼盖两侧自攻螺钉连接的数量进行估算.

3）采用退化四折线模型模拟组合楼盖的骨架

曲线，建立了组合楼盖面内刚度的计算方法，与试验结果吻合较好.

4）冷弯薄壁型钢-石膏基自流平砂浆组合楼盖为刚性楼盖，水平荷载在组合墙体之间的分配关系是按照墙体自身刚度的比值进行分配的.

参考文献

[1]    COUNTRYMAN D. Lateral tests on plywood sheathed diaphragms： Laboratory Report No.55[R]. Tacoma，WA： Douglas-fir Plywood Association，1952：1—15.

[2]   COUNTRYMAN D，COLBENSON P. Horizontal plywood diaphragm tests：Laboratory Report No.63 [R]. Tacoma，WA：Douglas-fir Plywood Association，1954：1—13.

[3]    BOTT J W. Horizontal stiffness of wood diaphragms [D]. Blacksburg，Virginia：College of Architecture and Urban Studies of Virginia Polytechnic Institute and State University，2005：1—85.

[4]    TISSELL J R，ELLIOTT J R. Plywood diaphragms：Laboratory Report No.138 [R]. Tacoma，WA：American Plywood Association，1997：1—21.

[5]    NIKOLAIDOU V，LATREILLE P，LIGNOS D G，et al. Seismic performance characterization of wood-sheathed and cold-formed steel framed floor and roof diaphragm structures[J]. Journal of Structural Engineering，2018，144（2）：04017215—1—04017215—11.

[6]    CHATTERJEE A，ARWADE S R，SCHAFER B W，et al. System reliability of floor diaphragms framed from cold-formed steel with wood sheathing [J]. Journal of Structural Engineering，2018，144（2）：04017208—1—04017208—12.

[7]    LOSS C，FRANGI A. Experimental investigation on in-plane stiffness and strength of innovative steel-timber hybrid floor diaphragms [J]. Engineering Structures，2017，138：229—244.

[8]    馬仲，何敏娟，马人乐. 轻型钢木混合楼盖水平抗侧性能试验[J].振动与冲击，2014，33（18）：90—95.

MA Z，HE M J，MA R L. Tests for a light wood-steel hybrid diaphragm′s anti-racking performance [J]. Journal of Vibration and Shock，2014，33（18）：90—95. （In Chinese）

[9]    管宇，周绪红，石宇，等. 冷弯薄壁型钢-石膏基自流平砂浆组合楼盖面内受力性能研究[J].建筑结构学报，2017，38（S1）：17—24.

GUAN Y，ZHOU X H，SHI Y，et al. Study on in-plane mechanical behavior of cold-formed thin-walled steel-gypsum based self-leveling mortar composite floor [J]. Journal of Building Structures，2017，38（S1）：17—24. （In Chinese）

[10]  石宇，周绪红，管宇，等. 冷弯薄壁型钢-石膏基自流平砂浆组合楼盖滞回性能试验研究[J].建筑结构学报，2018，39（4）：110—118.

SHI Y，ZHOU X H，GUAN Y，et al. Experimental study on hysteretic behaviors of cold-formed thin-walled steel-gypsum based self-leveling mortar composite floor [J]. Journal of Building Structures，2018，39（4）：110—118. （In Chinese）

[11]  管宇，周绪红，石宇. 冷弯薄壁构件与组合板螺钉连接推出试验研究[J].哈尔滨工程大学学报，2018，39（5）：799—805.

GUAN Y，ZHOU X H，SHI Y. Push-out experimental study on screw connections between cold-formed steel components and composite slab [J]. Journal of Harbin Engineering University，2018，39（5）：799—805. （In Chinese）

[12]  管宇.冷弯薄壁型钢-石膏基自流平砂浆组合楼盖面内受力性能研究[D]. 西安：长安大學建筑工程学院，2016：112—129.

GUAN Y. Study on the in-plane mechanical behavior of cold-formed thin-walled steel-gypsum based self-leveling mortar composite floor [D]. Xi′an：School of Civil Engineering，Chang′an University，2016：112—129. （In Chinese）

[13]  张劲，王庆扬，胡守营，等. ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构，2008，38（8）：127—130.

ZHANG J，WANG Q Y，HU S Y，et al. Parameters verification of concrete damaged plastic model of ABAQUS [J]. Building Structures，2008，38（8）：127—130. （In Chinese）

[14]  JGJ 227—2011 低层冷弯薄壁型钢房屋建筑技术规程[S].北京：中国建筑工业出版社，2011：29—36.

JGJ 227—2011 Technical specification for low-rise cold-formed thin-walled steel buildings [S]. Beijing：China Architecture and Building Press，2011：29—36. （In Chinese）

[15]  GB 50011—2010 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2016：19—32.

GB 50011—2010 Code for seismic design of buildings [S]. Beijing：China Architecture and Building Press，2016：19—32. （In Chinese）

[16]  石宇，周绪红，聂少锋，等.冷弯薄壁型钢组合墙体的抗震性能研究[J].土木工程学报，2010，43（S1）：124—129.

SHI Y，ZHOU X H，NIE S F，et al. Research on the seismic performance of cold-formed steel stud wall [J]. China Civil Engineering Journal，2010，43（S1）：124—129. （In Chinese）