不同锈蚀程度下Q235钢框架梁恢复力模型研究

郑山锁 刘晓航 张晓辉 贺金川 刘毅

摘   要：为研究不同锈蚀程度下Q235钢框架梁的力学性能，基于Q235钢框架梁抗震性能试验，通过对6根锈蚀程度不同钢框架梁试件的低周反复荷载试验，根据试验结果得到其滞回曲线、骨架曲线及刚度退化规律，分析试验数据得到不同锈蚀程度对钢框架梁抗震性能的影响.引入循环退化指数 ，拟合了具有累计损伤效应的特征点（屈服点、极限点、破坏点）公式，提出了适用于锈蚀钢框架梁的滞回规则，进而建立了考虑锈蚀作用的钢框架恢复力模型. 其中3根试件进行模拟曲线与试验曲线的对比，另3根试件进行模拟曲线与有限元分析的对比，对比结果表明恢复力模型有较高的精度，吻合情况良好，所建恢复力模型可为不同锈蚀程度的钢框架梁分析提供理论依据，为钢框架梁在不同锈蚀程度下的弹塑性分析奠定了基础.

关键词：低周反复加载;钢框架梁;锈蚀;重复荷载;循环退化;恢复力模型

中图分类号：TU391;TU317.1                文献标志码：A

文章编号：1674—2974（2019）09—0044—10

Abstract： To study the mechanical properties of Q235 steel frame girder in different corrosion degrees， low frequency cyclic loading test on steel frame girders of six trusses in different corrosion degrees was carried out on the basis of seismic performance test of steel frame girders. The hysteresis curve， skeleton curve and rigidity degeneration rule were obtained based on the text results. The effect of different corrosion degrees on seismic performance of steel frame beams was acquired by analyzing text data. The cyclic degradation index was introduced， and the characteristic point （yield point， limit point and breaking-down point） formula with cumulative damage effect was fitted. The hysteretic rule applied to rusted steel frame girders was put forward，and then the restoring force model of steel frame with the consideration of corrosive action was established. The comparison between the simulation curve and text curve for the samples of three trusses was performed， and the comparison between the simulation curve and finite element analysis for other samples of three trusses was implemented. The comparison results show that the restoring force model has high precision and better tally， the established restoring force model can provide theoretical basis for the analysis on steel frame girders in different degree of corrosion and lay a foundation for elastic-plastic analysis steel frame girder in different degree of corrosion

Key words： low cyclic loading;steel frame girder;corrosion;cyclic loading;cyclic degradation;restoring force model

鋼结构在地震作用下发生一系列非线性反应，如钢材的屈服、结构内力的变化以及结构的变形等. 为了更充分地研究地震过程中结构力学性能的变化过程，必须构建在反复荷载作用下截面或材料性能变化的准确本构关系，即恢复力模型[1]. 恢复力模型是在结构或构件弹塑性反应分析时，为能更准确地反映结构的宏观动力特性，而基于大量试验数据和理论分析结果建立的分析模型[2]. 恢复力模型是结构在地震反复荷载作用下展现的定量数学关系，可以是弯矩和曲率的关系，也可以是荷载和位移的关系.恢复力模型能够直观地反映结构或构件的某些关键性能，如强度的退化和刚度的衰减，结构或构件在耗能和延性方面的变化等[3].

目前，对完好结构或构件的恢复力已进行了大量的试验及研究，建立了相应的恢复力模型[4-6]. 由于实际钢结构或构件普遍存在不同程度的侵蚀情况，导致与完好结构或构件的变化规律有所区别，不同锈蚀程度结构或试件的滞回曲线存在明显的差异.目前的研究成果未考虑到钢框架梁锈蚀后结构不同锈蚀程度的影响和结构锈蚀后钢框架梁刚度退化的影响.基于此，本研究对不同锈蚀程度下Q235钢框架梁试件进行试验和分析建模，建立考虑锈蚀影响的钢框架梁的恢复力模型，准确地描述锈蚀钢框架梁各项性能的退化情况，为研究不同锈蚀程度下钢框架梁的刚度变化及滞回性能提供理论依据.

1   试验概况

1.1   试件设计与制作

本试验参考《建筑抗震设计规范》GB 50011—2010，采用1 ∶ 2的缩尺比例设计了6根钢框架梁试件，锈蚀程度分为6个级别. 试件均采用热轧H型钢制作，材料为Q235B，钢框架梁规格为300 mm ×150 mm×6.5 mm×9 mm，并在钢梁底端安置相对刚度较大的底梁，起到固定支座的作用，试件详细尺寸如图1所示. 选择钢材锈蚀时间作为控制变量，以失重率作为量化指标，试件具体设计参数见表1.

1.2   试验装置及加载制度

试验在本校的结构工程与抗震教育部重点实验室进行，采用悬臂梁式加载方案，30 t电液伺服作动器在梁端施加水平往复荷载.在试验开始前用压梁固定底梁的梁端限制其平面内自由度，同时在底梁两端分别安设顶梁及千斤顶，这样可以有效地避免因滑移造成的侧向失稳，在试件两侧设置侧向支撑用以防止试件发生平面外失稳.钢框架梁的荷载-位移试验数据由MTS系统自动采集，在试件主要控制截面的翼缘及腹板上布置电阻应变片以考察整个受力过程中应变的发展规律. 试验加载装置如图2所示.

考虑到数据采集和后期处理的工作量，為了更准确地获得试件的屈服点、峰值点和破坏点及其各自对应的荷载和位移等信息，综合考虑到每种加载方法的优劣性，最终采取基于位移的加载制度，如图3所示. 在试件正式加载前，应先将试件进行预加载，目的是减少试件内部的不均匀性，使荷载与变形关系趋于稳定，同时检查试验装置及仪器仪表工作是否正常.加载过程中每级位移5 min内循环加载2次，预加反复荷载值不应超过试件屈服点理论计算值的30%[7].

1.3   现象及破坏模式

在低周往复荷载作用下，不同锈蚀时间的试件均经历了弹性阶段、弹塑性阶段和破坏阶段. 前三级位移，试件均处于弹性阶段. 位移级别加载到15 mm左右时试件进入弹塑性阶段;位移级别加载到60 mm时，试件B-1～B-5达到最大承载力，试件B6相对于B-1～B-5的最大承载力位移点下降25.18%，为44.89 mm;当位移级别加载到90 mm正向第一圈时试件发生破坏.在弹塑性阶段试件均为左右翼缘屈曲后发生腹板屈曲，梁底部形成塑性铰，承载力开始下降.随后出现不同程度的构件裂缝、铁锈层脱落直至试件破坏，试件发生破坏过程较为缓慢且耗能性较好，属于延性破坏，如图4所示.

此外，由于锈蚀程度不同，各试件加载破坏过程又有所差异，具体表现为：随锈蚀程度增大，处于弹性阶段的加载位移下降，试件最大承载力及其位移下降.发生翼缘屈曲时，屈曲位置与梁底距离增大，试件破坏程度随锈蚀程度的增大逐渐增高.

1.4   滞回曲线

滞回曲线能够充分反映试件加载过程中结构承载力和各个特征点的变化情况;同时滞回曲线的饱满度可以反映结构的耗能能力，从而反映其抗震性能的优劣性，总的来说滞回曲线越饱满，结构的耗能性与抗震能力越好[8-9].

图5给出了各试件荷载-位移滞回曲线，可知：

1）位移级别在15 mm内时试件处于弹性阶段，加载过程中试件没有明显变化，卸载后基本没有残余变形.

2）在加载中期，随着位移级别和循环次数的增加，翼缘、腹板等部位逐渐屈服且塑性变形逐渐增大，试件刚度发生不同程度的退化，荷载卸为零时，试件呈现残余变形.反映在荷载-位移滞回曲线上则是曲线包围面积逐渐增大.

3）试件B-1～B-6的荷载-位移曲线均较为饱满，

未出现捏缩现象，呈明显的纺锤形，且滞回曲线包围的面积较大，由此可以看出，钢梁拥有较好的延性与耗能能力.同时随着锈蚀程度的增大，试件的峰值荷载及其曲线饱满度有所下降.

1.5   骨架曲线

骨架曲线在弹塑性分析中占据非常重要的地位，能够集中反映试件的屈服位移、屈服荷载、峰值位移、峰值荷载、极限位移和极限承载力的变化. 对比不同锈蚀程度骨架曲线可得出一般性规律[10]，不同锈蚀程度钢框架梁的骨架曲线见图6.

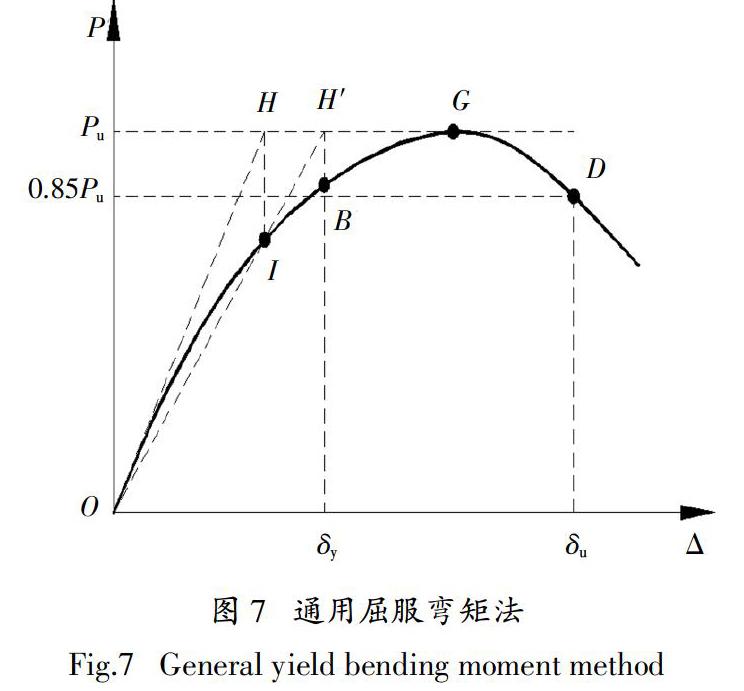
试件的屈服荷载、屈服位移、极限荷载和极限位移等性能指标可以从试件的骨架曲线上获取，采用通用屈服弯矩方法的原理确定屈服点，如图7所示 [11].

由图7可以得到以下结论：

1）在低周往复荷载作用下，钢框架梁基本经历了三个阶段，分别为弹性阶段、弹塑性阶段和破坏阶段.试件在加载初期处于弹性阶段时，骨架曲线符合线性发展. 随着加载位移级别的增大，骨架曲线呈现非线性发展趋势，达到屈服点且出现了拐点，试件的抗侧移刚度降低，进入弹塑性阶段.当加载位移级别进一步增大时，加载荷载达到峰值，随后曲线开始出现下降段，继续加载至试件发生破坏.

2）不同锈蚀程度的试件，骨架曲线在加载初期基本重合，因为加载初期试件处于弹性阶段.但随着加载位移的增大，试件出现了不同程度的刚度退化，骨架曲线开始出现了差异，且锈蚀程度越大差异越明显，试件的屈服荷载、峰值荷载、极限承载力均有所下降.

对比表2中的6个试件可以看出，不同锈蚀程度试件的承载力均发生了变化.锈蚀程度越大，耗能能力下降越大，同时下降速率增大.锈蚀对试件刚度也产生了影响，锈蚀程度越大，试件的屈服点、峰值点、极限点的位移和荷载，以及延性系数越小，试件抗变形能力减弱，延性变差.

1.6   刚度退化

位移级别和循环次数的增加也会造成试件的刚度退化，刚度退化和强度退化都是衡量与评价结构或构件抗震性能的指标[12]. 根据《建筑抗震试验方法规程》（JGJ 101—96）[13]中所述方法，定义试件滞回曲线中原点和某次循环中峰值荷载点连线的斜率来表征试件的退化.分析图8所示的刚度退化曲线，可以得到如下结论：

由图14和图15可以看出，通过计算所得的滞回曲线和试验结果、有限元分析有较高吻合度，可以近似反映出不同锈蚀程度试件的抗震性能.但是通过计算得到的滞回曲线正、反方向的偏差不大，与实际试验不符，这是因为在建立本文的恢复力模型中没有考虑正、反方向骨架曲线不对称而导致的.

3   结   论

本文以6根不同锈蚀程度的Q235钢框架梁作为研究对象，采用现有骨架曲线特征点计算方法拟合了不同锈蚀程度试件的计算特征点公式.在Ibarra-Krawinkler（IK）滞回模型基础上建立了考虑锈蚀因素的恢复力模型，并进行验证. 结果表明该恢复力模型可以描述试件在低周反复荷载下的材料的非线性特性，为此种试件不同锈蚀程度的弹塑性分析奠定了基础.基于以上研究得到以下结论：

1）将完好的钢框架梁试件的骨架曲线简化为考虑下降段的三折线模型，结合该模型给出了试件三个特征点的理论推导公式.

2）恢复力模型的特征点计算值与试验数据及其有限元分析吻合较好，故而该恢复力模型可以用来模拟此类试件.

3）基于Ibarra-Krawinkler（IK）模型并考虑不同锈蚀程度的恢复力模型既能较为准确地描述由于循环加载引起的强度、刚度的循环退化，又能考虑由于锈蚀损伤引起的退化速率的变化.

4）引入循环退化指数，建立了能够考虑循环退化效应的锈蚀钢框架梁恢复力模型.计算滞回曲线与试验滞回曲线吻合较好，能够真实反映锈蚀钢框架梁的滞回性能，在一定程度上验证了该恢复力模型的适用性.研究成果为在役钢框架结构非线性地震反应分析提供了理论依据.

参考文献

[1]    党争，梁兴文，代洁，等. 考虑损伤的纤维增强混凝土剪力墙恢复力模型研究[J]. 工程力学，2016，33（5）：124—133.

DANG Z，LIANG X W，DAI J，et al. Study on restoring force model of fiber reinforced concrete shear wall considering damage index [J]. Engineering Mechanics，2016，33（5）：124—133.（In Chinese）

[2]    郭子雄，杨勇. 恢复力模型研究现状及存在问题[J]. 世界地震工程，2004，20（4）：47—51.

GUO Z X，YANG Y. State-of-the-art of restoring force models for RC structures [J]. World Earthquake Engineering，2004，20（4）：47—51.（In Chinese）

[3]    唐昌辉，倪佳，程明慧. 无黏结部分预应力砼梁恢复力模型的研究[J].湖南大学学报（自然科学版），2016，43（11）：55—60.

TANG C H，NI J，CHENG M H. Research on restoring force model of unbonded partially prestressed concrete beams [J]. Journal of Hunan University （ Natural Sciences），2016，43（11）：55—60.（In Chinese）

[4]    冉红东，赵道程，梁文龙，等. 延性交错桁架钢框架双槽钢组合H型截面弦杆恢复力模型研究[J]. 西安建筑科技大学学报（自然科学版），2017，49（1）：56—63.

RAN H D，ZHAO D C，LIANG W L，et al. Study on restoring force model of steel double-channel built-up chords of special staggered truss steel frame structure [J]. Journal of Xi′an University of Architecture & Technology （Natural Science Edition），2017，49（1）：56—63. （In Chinese）

[5]    過镇海. 钢筋混凝土原理[M]. 3版. 北京：清华大学出版社， 2013：104—114.

GUO Z H. Reinforced concrete principle [M]. 3rd ed. Beijing：Tsinghua University Press，2013：104—114. （In Chinese）

[6]    郑山锁，朱揽奇，牛丽华，等. 酸雨腐蚀砖墙抗震性能试验及恢复力模型研究[J]. 土木工程学报，2017，50（4）：21—31.

ZHENG S S，ZHU L Q，NIU L H，et al. Experiment and restoring force model research on seismic behavior of brick walls affected by acid rain corrosion [J]. China Civil Engineering Journal，2017，50（4）：21—31. （In Chinese）

[7]    JGJ/T 101—2015 建筑抗震试验规程[S]. 北京：中国建筑工业出版社，2015：10—16.

JGJ/T 101—2015 Specificating of testing methods for earthquake resistant building [S]. Beijing：China Architecture & Building Press，2015：10—16. （In Chinese）

[8]    郑山锁，左英，张晓辉，等. 酸性大气环境下多龄期平面钢框架结构抗震性能试验研究[J]. 工程力学，2017，34（9）：73—82.

ZHENG S S，ZUO Y，ZHANG X H，et al. Experimental research on the seismic behavior of multi-aged planar steel frames under acidic atmospheric environment [J]. Engineering Mechanics，2017， 34（9）：73—82. （In Chinese）

[9]    汪梦甫，杨冕. 端部带肋方钢管混凝土柱抗震试验研究[J]. 湖南大学学报（自然科学版），2017，44（11）：31—37.

WANG M F，Y M. Experimental study on seismic behavior of square concrete-filled steel tube column with end ribs [J]. Journal of Hunan University （Natural Sciences），2017，44（11）：31—37. （In Chinese）

[10]  齐岳，郑文忠.低周反复荷载下核心高强混凝土柱抗震性能试验研究[J]. 湖南大学学报（自然科学版），2009，36（12）：6—12.

QI Y，ZHENG W Z. Experimental study of the seismic behavior of concrete columns with high strength core under low cyclic loading [J]. Journal of Hunan University （Natural Sciences），2009，36（12）：6—12. （In Chinese）

[11]  姚谦峰. 土木工程结构试验[M]. 2版. 北京：中国建筑工业出版社，2008：224—245.

YAO Q F. Civil engineering structure test [M]. 2nd ed. Beijing：China Architecture & Building Press，2008：224—245. （In Chinese）

[12]  郑山锁，张晓辉，王晓飞，等. 近海大气环境下多龄期钢框架柱抗震性能的试验研究[J]. 土木工程学报，2016，49（4）：69—77.

ZHENG S S，ZHANG X H，WANG X F，et al. Experimental research on seismic behaviors of multi-aged steel frame columns in the offshore atmospheric environment [J]. China Civil Engineering Journal，2016，49（4）：69—77. （In Chinese）

[13]  JGJ 101—96建筑抗震試验方法规程[S]. 北京：中国建筑工业出版社，1997：9—16.

JGJ 101—96 Architectural seismic test method procedure [S]. Beijing：China Architecture & Building Press，1997：9—16. （In Chinese）

[14]  殷小溦，吕西林，卢文胜. 配置十字型钢的型钢混凝土柱恢复力模型[J]. 工程力学，2014，31（1）：97—103.

YIN X W，L X L，LU W S. Resilience model of src columns with cross-shaped encase steel [J]. Engineering Mechanics，2014，31（1）：97—103. （In Chinese）

[15]  施炜，陆新征，叶列平，等. 建筑结构倒塌分析的单自由度模型[J]. 工程力学，2012，29（10）：5—12.

SHI W，LU X Z，YE L P，et al. Single-degree-of-freedom hysteretic model for collapse analysis of building structures [J]. Engineering Mechanics，2012，29（10）：5—12. （In Chinese）

[16]  RAHNAMA M，KRAWINKLER H. Effects of soft soil and hysteresis model on seismic demands [R]. Palo Alto：Stanford University，Blume Earthquake Engineering Center，1993：34—37.

[17]  郑山锁，张晓辉，黄威曾，等. 近海大气环境下锈蚀平面钢框架抗震性能试验研究及有限元分析[J]. 工程力学，2018，35（7）：62—73.

ZHENG S S，ZHANG X H，HUANG W C，et al. Experimental research and finite element analysis of the seismic behavior of corroded plane steel frames under offshore atmospheric environment [J]. Engineering Mechanics，2018，35（7）：62—73. （In Chinese）