易卦与代数

丁光涛

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241003)

引 言

《易经》是我国一部重要的古代典籍，其有一个抽象的符号体系：两爻——四象——八卦——六十四卦，几千年的传承、阐发、研究和应用，与这个符号体系相关联，形成一个内容庞大而又条理分明，要素简单却能包罗万象的学术体系，用以说明自然、社会和人生，直到现代仍有众多学者对其进到广泛而深入的研讨，其中包括与现代自然科学相关的研究[1-4]。历史上，《易经》研究与数学紧密相关，重要的研究领域之一是象数学说，近几十年考古发现表明，易卦符号体系与数的关系源远流长，早在商周时期就有由数字写成的易卦，即数字卦的存在[5]。在20世纪的科学易研究的一个重要方面是将现代数学知识与传统易卦学说联系起来，这种研究代表性的成果就是易卦体系可以与数学上的二进位制之间相联系[6,7]。最近，我们讨论了六十四卦的三种构成方式，指出易卦体系也可以与四进位制、八进位制相对应[8]。本文将从代数角度来研究易卦体系[9，10]，引入几种不同的共轭运算和乘法，并将两爻、四象和八卦与通常的实数、复数和四元数等数系的“基数”联系比较，得到一个结论，即以四象和八卦为“基数”，可以构成与复数、四元数并行但是又不同的数系。然后，将四象和八卦的代数运算推广到六十四卦。现代社会进入数字时代，算法起着越来越重要的作用，相当数系的出现，会导致新的算法出现，这就是说，这种基于易卦的代数研究，可能对于数字社会和信息技术的发展具有相当重要的意义。

2 两爻四象八卦的共轭运算和乘法运算

2.1 爻和卦的共轭运算

前人在研究卦象时发现，这些卦“二二相耦，非覆即变”。所谓“覆”，即将卦象中全部爻位颠倒；所谓“变”，即将卦象中每个爻的阴阳互变。

基于这种观念，我们引入八卦的三种“共轭”变换：(1)阴阳共轭变换，即将每爻的阴阳性质互变；记以*，

这种八卦的“二二相耦，非覆即变”，同样适合于四象，故对于四象也能够引入上述三种共轭变换。

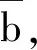
对八卦为

2.2 四象和八卦的直接乘法运算

在引入共轭变换后，进一步引入卦象的乘法运算。由四象，八卦的构成可以确定，爻的乘法运算是基础，爻的乘法规定为：

利用上述字母记法，可以将爻的乘法写成

e·e=e，ē·ē=e，e·ē=ē·e=ē

在爻的乘法基础上定义四象、八卦的乘法，最简单的是直接乘法，其乘积由对应爻位上爻的乘积决定，记为“•”，例如：

利用字母符号记法，上述直接乘法写成

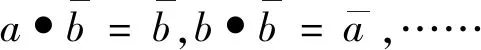
两爻、四象和八卦的直接乘法规则可以用乘积表表示如下：

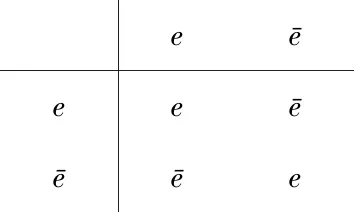
表1 两爻直接乘积表

表2 四象直接乘积表

表3 八卦直接乘积表

引入直接乘积法后可见，四象(八卦)的阴阳共轭就是对应的四象(八卦)与太阴(坤卦)的直接乘积。还容易验证，四象和八卦的直接乘积满足交换律和结合律，在直接乘法规则下，四象和八卦分别构成两个对易群，群中单位元分别是太阳a和乾卦E，每一个四象和八卦都是自身的逆元。

3 四象和八卦的其他乘法

在上述直接乘法基础上，结合几种共轭运算，可以引入其他几种乘法。以八卦为例说明如下：

(1)阴阳共轭乘法，以⊙表示。两个八卦的阴阳共轭乘积等于被乘八卦与相乘八卦的阴阳共轭的直积，容易验证，两个八卦的阴阳共轭乘积等于两个相乘八卦的直积的阴阳共轭。如

对于这种乘法以后不拟详细讨论。

(2)转置共轭乘法，以×表示。两个八卦的转置共轭乘积等于被乘的八卦与相乘八卦的转置共轭的直积，如：

这种乘法一般不满足交换律和结合律。

(3)复合共轭乘法，以⊗表示。两个八卦的复合共轭乘积等于被乘的八卦与相乘八卦的复合共轭的直积，如

这种乘积也不满足交换律与结合律。

下面比较详细地讨论四象和八卦的转置共轭乘积，对应的乘积表如下：(表中行元素为被乘之素)

表4 四象转置共轭乘积表

将表2、表3与表4、表5比较，可以看出直接乘法与转置共轭的乘法之间的区别。已经指出直接乘法满足交换律和结合律，在多个四象或八卦连续相乘时，这种性质说明这些相乘的四象或八卦的顺序是无关紧要的，但是，对于转置共轭乘法，交换律与结合律

表5 八卦转置共轭乘积表

不成立，这时多个连乘的四象或八卦的顺序就至关紧要了，它们的改变会导致结果的不同的。在这种多个元素连乘时，才能表明为什么在定义转置共轭乘法中，是取后面相乘的四象或八卦作转置共轭后，再与前面被乘的四象或八卦作直接相乘，因为这样规定才是合理的可行的。

4 基于四象八卦构成的新数系

数学上实数、复数和四元数的“基数”及其相反数分别是：1和-1；l，i，-i，-l；l，i，j，k，-i，-j，-k，-l。这些“基数”的乘法表如下：

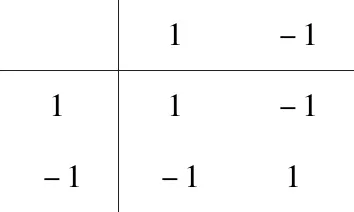
表6 实数系基数乘法表

表7 复数系基数乘法表

表8 四元数系基数乘法表

如果试图把两爻、四象、八卦与上述三种数系的基数作如下对应：

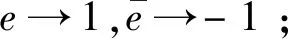
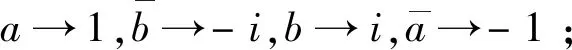
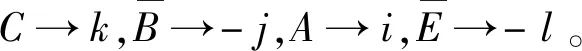
那么将发现，只有表1与表6与上述对应相符合，而表2和表3，或表4和表5，都与表7和表8不相符合，换句话说，可以认为两爻与实数的基数相对应，但是不能把四象和八卦与复数和四元数的基数对应起来。

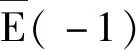
5 将共轭与乘法运算推广到六十四卦

5.1 六十四卦的共轭变换

六十四卦的阴阳共轭可以直接从八卦推广，即每爻的阴阳性质互变，仍然以*号标记。

多种构成六十四卦方式，导致定义六十四卦转置共轭变换也存在多种可能。第一种最简单直接，组成的六爻位序全部翻转，这是四象、八卦转置共轭的直接推广；第二种是组成的三个四象，上下位互换，中位不动，但每个四象内的爻位不转置；第三种是上下经卦互换，且每个经卦(八卦)内的爻卦不转置，等等。显然，这三种转置共轭的结果有相同有不同。这里为了转置共轭定义简单明确，而且与四象、八卦的转置共轭一致，约定六十四卦的转置共轭采用第一种方式，以符号T标记。

确定了转置共轭定义后，六十四卦的复合共轭就是将阴阳共轭与转置共轭组合起来，即组成六十四卦的六爻，全部阴阳互变，而且爻位全部翻转，这种复合共轭仍然以符号+标记。

5.2 六十四卦的直接乘法和转置共轭乘法

六十四卦的乘法也只讨论两种；第一种是直接乘法，两卦的直接乘积由六个对应爻位上的两爻直接乘积决定。例如，家人卦与既济卦直积是夬卦，节卦与旅卦直积是坤卦：

第二种是转置共轭乘法，由两卦的乘积是被乘的六十四卦与相乘的六十四卦的转置共轭的直接乘积决定，如家人卦与既济卦的转置共轭乘积为剥卦，节卦与旅馆的转置共轭乘积为颐卦：

显然，只有第一种直接乘法是可交换可结合的，对这种乘法六十四卦构成一个可交换群，单位元是乾卦，每一卦的逆元都是自身。

6 结论与讨论

本文循着近世代教的观念和方法，对传统的易卦进行新的探讨和阐释：

(1)对四象和八卦引入三种共轭运算：阴阳共轭、转置共轭和复合共轭。

(2)定义两爻乘积，在此基础上，结合共轭运算，定义四象和八卦的乘法运算，重点讨论了两种：直接乘法和转置共轭乘法。

(3)将两爻、四象和八卦分别当作某些数系的“基数”，发现与两爻对应的是实数系，但是，与四象和八卦对应的数系，则分别与复数系和四元数系形似而实不同，但是，可以在四象和八卦作为基数的假设下，引入新的数系，这两种新的数系可以看作实数系的推广。

(4)将上述共轭运算和两种乘法推广到六十四卦。

以现代数学概念和方法来探讨易卦，能够启迪新的数学思想，能够产生新的数学成果。例如，可以发展二进位制、四进位制、八进位制，这些进位制与传统十进位制不同，但并行不悖，且在新的信息技术科学中获得重要应用。这种研究在当代更有其必要，古代希腊毕达哥拉斯学派认为“一切皆数”，在后工业化社会，“一切皆信息”，信息表现为数据，故在一定程度上可以说，一切能够表示为数据，算法的价值空前提高。如果能够在数的基本领域研究上有所突破，观念上有所创新，那么一定具有潜在的价值，故应当继续研究基于四象和八卦上的新的数系和算法，探索引入的易卦代数在科技领域中可能的应用。

此外，研究易卦结构与排序问题时，已经发现六十四卦与遗传因子之间的对应[11-13]，还可以在六十四卦与轻子夸克之间建立对应关系[13]，以及其它的众多与自然科学技术相关的探索[14,15]，都显示出传统的易经学说可能对现代科学技术研究有启发和促进作用，所以不论当下的这些研究成果是多么不成熟，但这种借鉴中华传统智慧，探索新的科学技术的努力，都应当继续下去。