乳化液泵偏心曲轴变形特性分析及优化设计
屈小兵
(潞安集团 东盛煤业有限公司,山西 沁源 046500)
随着综采技术的不断发展与应用,乳化泵依靠其高流量、高压力、结构紧凑的特性,成为矿井集约高效生产的主要动力源之一。近年来,采煤机械设备逐渐向重型化、自动化、智能化方向发展,但是在综采设备的配套方面仍存在着许多缺陷,特别是在液压支护方面,由于受到各种工况条件的约束,使得采煤设备无法发挥应有的工作效率,从而不断制约着矿井经济的发展[1-2]。
乳化液泵作为液压支架的主要动力源,直接决定了工作面支架的工作特性与安全特性。在乳化液泵的配套安装期间,由于各部件的制作误差及人工安装偏差,时常会发生各种的传动异常现象,直接影响了乳化液泵的工作特性与使用寿命[3-4]。其中曲轴作为乳化液的最关键传动元件,在存在偏心现象时,会在高流量、高压力、不平衡惯性力等因素的长时间作用下产生疲劳断裂,直接影响正常生产。为有效提高乳化液泵曲轴的工作效率,增强使用寿命,应当以仿真模拟的方式对其变形量与应力大小进行分析,并提出合理的优化方案。
1 曲轴运动原理分析
本文研究对象为三拐四支撑式乳化液泵,从动力输入端起,四个轴承型号依次为:第一个:双列调心滚子轴承23220cc/w33(100 mm×180 mm×60.2 mm),第二、三个双列调心滚子轴承23032cc/w33(160 mm×240 mm×60 mm),第四个:圆柱滚子轴承2316EC(80 mm×170 mm×58 mm)。曲轴正常工作时,在连杆带动下进行往复式柱塞传动,曲柄进行绕固定点的旋转运动。当曲柄顺时针旋转至0°~180°时,柱塞左移,将乳化液推入工作端;旋转至180°~360°时,柱塞进行右移,并受负压推动进行吸液。
如图1所示,曲轴以O为旋转中心,A点为曲柄销与连杆的连接点,B点表示滑块上的柱销,即曲柄OA绕O点作旋转动作,连杆AB作平面运动,滑块B作沿CD方向的直线往复运动。ω为曲柄的旋转角速度,β为连杆的摆动角,L为连杆长,s为柱塞的位移距离,以θ=0°时为曲轴的初始状态,即滑块B位于D点处开始计量[5]。

图1 曲轴运动原理简图
曲拐在转角θ为0~180°时,柱塞进行排液运动,此时的缸内液压为41.2 MPa,当转角θ为180~360°时,柱塞开始吸液,缸内液压减小至2.4 MPa。柱塞每旋转60°曲轴工作状况都会发生变化,因此可以将柱塞每旋转60°作为一个步长,即每个步长为0.015 28 s。已知此类曲轴在理想状态的工作转矩为3 883 650 N·mm,角速度为68.55 rad/s,柱塞力为1.633×105N,为了进一步分析曲轴的危险截面,建立Ansys仿真模型。
2 模型建立及参数设定
通过Pro/engineer建立三拐四支撑式乳化液泵实物模型,并将曲轴部分导入Ansys workbench中,利用Geometry模块进行模型的计算与分析[6]。模型选取钢材为42CrMo钢,材料性能参数如表1所示。本次模拟模型为曲轴,属于不规则、非对称型模型,采用四面体单元网格进行划分,共生成64 362个节点,38 142个单元格,如图2所示。给定模型三个轴承处x轴、y轴位移量为零,z轴为自由端,第一轴承给定x轴、y轴、z轴位移量为零,第二、三轴承给定x轴、y轴位移量为零,z轴为自由端,第四轴承给定x轴位移0.03 mm、y轴位移0.04 mm、z轴为自由端[7]。模拟曲轴存在偏心力时,六种受力工况下的加载力,如表2所示。
3 模拟结果分析
为更好地对比不同工况下,曲轴的轴与轴承部分受力变形状况,根据曲轴的不同单拐受力情形以及不同双拐排液状况,对比分析曲轴的六种工况下的曲轴受力云图。六种工况分别为:工况1(曲拐1受力最大)、工况2(曲拐2受力最大)、工况3(曲拐3受力最大)、工况4(曲拐1和曲拐3同时受排液力)、工况5(曲拐2和曲拐3同时受排液力)、工况6(曲拐1和曲拐2同时受排液力)。通过Ansys workbench12中的Static structure模块对曲轴在六种工况下做静力分析,得到六组应力云图与应变云图。如图3~图8所示。

表1 曲轴钢材性能
表2不同工况下模型施加的加载力大小N
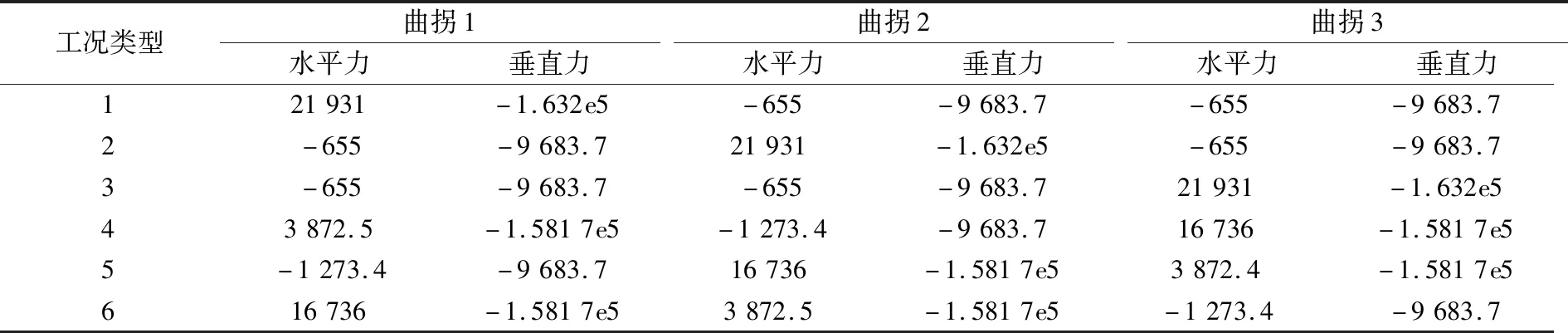
工况类型曲拐1水平力垂直力曲拐2水平力垂直力曲拐3水平力垂直力121931-1.632e5-655-9683.7-655-9683.72-655-9683.721931-1.632e5-655-9683.73-655-9683.7-655-9683.721931-1.632e543872.5-1.5817e5-1273.4-9683.716736-1.5817e55-1273.4-9683.716736-1.5817e53872.4-1.5817e5616736-1.5817e53872.5-1.5817e5-1273.4-9683.7

图2 曲轴模型网格划分


图3 工况1时的曲轴(存在偏心时)应变、应力云图
由图3可知,当曲轴处于工况1时,曲轴的变形位置为左端面、第一轴径、第三轴颈以及第四曲柄与右端轴的过渡圆角处,并且受力最大的部位为第四曲柄与右端轴的过渡圆角处。最大应力值为245.35 MPa,最大应变值为0.050 31 mm。


图4 工况2时的曲轴(存在偏心时)应变、应力云图
由图4可知,当曲轴处于工况2时,曲轴的变形位置为左端面、第二轴颈、第三轴颈以及第四曲柄与右端轴的过渡圆角处,并且受力最大的部位为第四曲柄与右端轴的过渡圆角处。最大应力值为246.92 MPa,最大应变值为0.050 32 mm。
由图5可知,当曲轴处于工况3时,曲轴的变形位置为曲轴左端面、第三轴颈以及第四曲柄与右端轴处,并且受力最大的部位为第四曲柄处。最大应力值为358.75 MPa,最大应变值为0.057 67 mm。
由图6可知,当曲轴处于工况4时,曲轴的变形位置为齿轮轴、第一轴颈、第三曲轴颈以及第四曲柄与右端轴,并且受力最大的部位为右端轴处。最大应力值为345.38 MPa,最大应变值为0.055 42 mm。


图5 工况3时的曲轴(存在偏心时)应变、应力云图


图6 工况4时的曲轴(存在偏心时)应变、应力云图
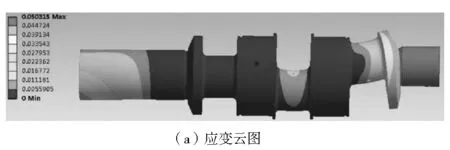
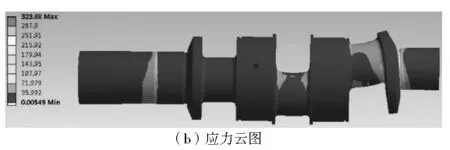
图7 工况5时的曲轴(存在偏心时)应变、应力云图
由图7可知,当曲轴处于工况5时,曲轴的变形位置为齿轮轴、第二轴颈、第三曲轴颈以及右端轴,并且受力最大的部位为右端轴处。最大应力值为323.88 MPa,最大应变值为0.050 3 mm。
由图8可知,当曲轴处于工况6时,曲轴的变形位置为齿轮轴、第二轴颈、第三曲轴颈以及右端轴,并且受力最大的部位为右端轴处。最大应力值为254.46 MPa,最大应变值为0.051 4 mm。



图8 工况6时的曲轴(存在偏心时)应变、应力云图
4 曲轴参数优化
通过曲轴的静态分析,当曲轴在安装过程中存在偏心时,曲轴在第三工况下受力情形最严重,且不满足曲轴的许用强度。因此,以曲轴处于工况3时的受力状况为背景,对其进行优化设计。由材料力学可知,当曲轴受力超出许用强度时,可以通过改变曲轴危险截面的受力面积来改善曲轴的变形状况。因此,采用Design Explorer对曲轴进行优化分析,以曲轴右端的轴径为参数输入端,以曲轴的最大应变为输出端,可以得到5种优化方案下的曲轴优化数据如图9所示[8]。

图9 曲轴优化输出结果
从图9中的五个设计点的输出结果来看,曲轴轴径设计为83.6 mm与82.1 mm时,输出的最大应力小于许用应力[σ],但设计点4的最大应力与许用应力较为接近,因此,选取轴径D为83.6 mm时较为适宜,且可将数值圆整至83 mm,能够有效缓解曲轴危险截面的应力状况,避免发生曲轴断裂以及过度疲劳损伤。
5 结 语
1) 通过建立仿真模型对曲轴在处于偏心情形时的危险截面进行了静力学分析,对比六种工况下的应力应变云图,得出第三工况下的曲轴所受应力值最大,且危险截面的位置为第四曲柄处。
2) 针对曲轴截面面积不足,提出了五种优化尺寸,并且通过Design Explorer输出五种尺寸大小对应的最大应力,最终确定右端曲轴的最佳设计轴径应为83 mm。
3) 采用优化后的曲柄尺寸能够满足曲柄的强度要求,有效避免曲轴在偏心情形下时的断裂或者变形现象,可大大提高曲轴的使用寿命。

