斜盘式轴向柱塞泵柱塞运动学分析的一般模型

王建森, 曹伟栋, 何鑫龙, 王峥嵘,2, 张志伟

(1. 兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2. 甘肃省流体机械及系统重点实验室, 甘肃 兰州 730050)

斜盘式轴向柱塞泵因结构紧凑、变量响应快、功率密度和效率高等优点在工业各领域得到广泛应用[1].一般斜盘式轴向柱塞泵柱塞与传动轴为平行布置结构，斜盘也仅有一个方向的倾角[2-4].随着柱塞泵技术指标的不断提高及变工况要求，斜盘式轴向柱塞泵的基本结构也在不断演化.某些泵型的柱塞在结构布置时与传动轴呈一定夹角，也叫柱塞倾角，该结构使得缸体配流端径向尺寸变小，从而可以降低缸体配流面摩擦副之间的相对运动线速度[5-8].也有些泵型在斜盘结构中采用了斜盘第二倾角技术，即斜盘相对互相垂直的两个轴分别有一个倾斜角，亦称为斜盘交错角技术，该结构有利于变工况下降低泵的流量脉动，改善泵的振动噪声特性[9-12].在已出版文献中，柱塞与传动轴平行布置和倾斜布置时柱塞的运动学分析模型结论一致，但对于斜盘有两个方向倾角时柱塞的运动学分析模型在文献[12]和文献[13]中却并不一致，存在疑惑.因此，为进一步验证斜盘有两个方向倾角时柱塞的运动学分析模型，并为综合考虑斜盘两个方向倾角和柱塞倾角新结构特征的研发服务，本文采用坐标变换法，推导出了斜盘式轴向柱塞泵柱塞运动学分析的一般数学模型，可为该结构泵的进一步研究奠定理论基础.

1 数学建模

斜盘式轴向柱塞泵结构简图如图1所示，主要由泵体、泵芯等组成，泵芯主要包括缸体、配流盘、滑靴柱塞组件、回程机构等，配流盘与斜盘支撑在泵体上.原动机动力由传动轴输入，通过与缸体花键连接，带动缸体、滑靴柱塞组件旋转;同时，在回程机构即中心弹簧、球铰及回程盘的作用下，滑靴柱塞组件沿斜盘平面滑动;由于斜盘为倾斜布置，故柱塞做复合运动,即随缸体的旋转运动和沿缸体孔轴线相对缸体的往复运动.取斜盘倾角为零度时各柱塞球头球心所在平面与传动轴轴线的交点o为坐标系原点，按右手系建立参考坐标系，x轴正向与纸面垂直朝外，y轴正向向下，z轴正向朝右.

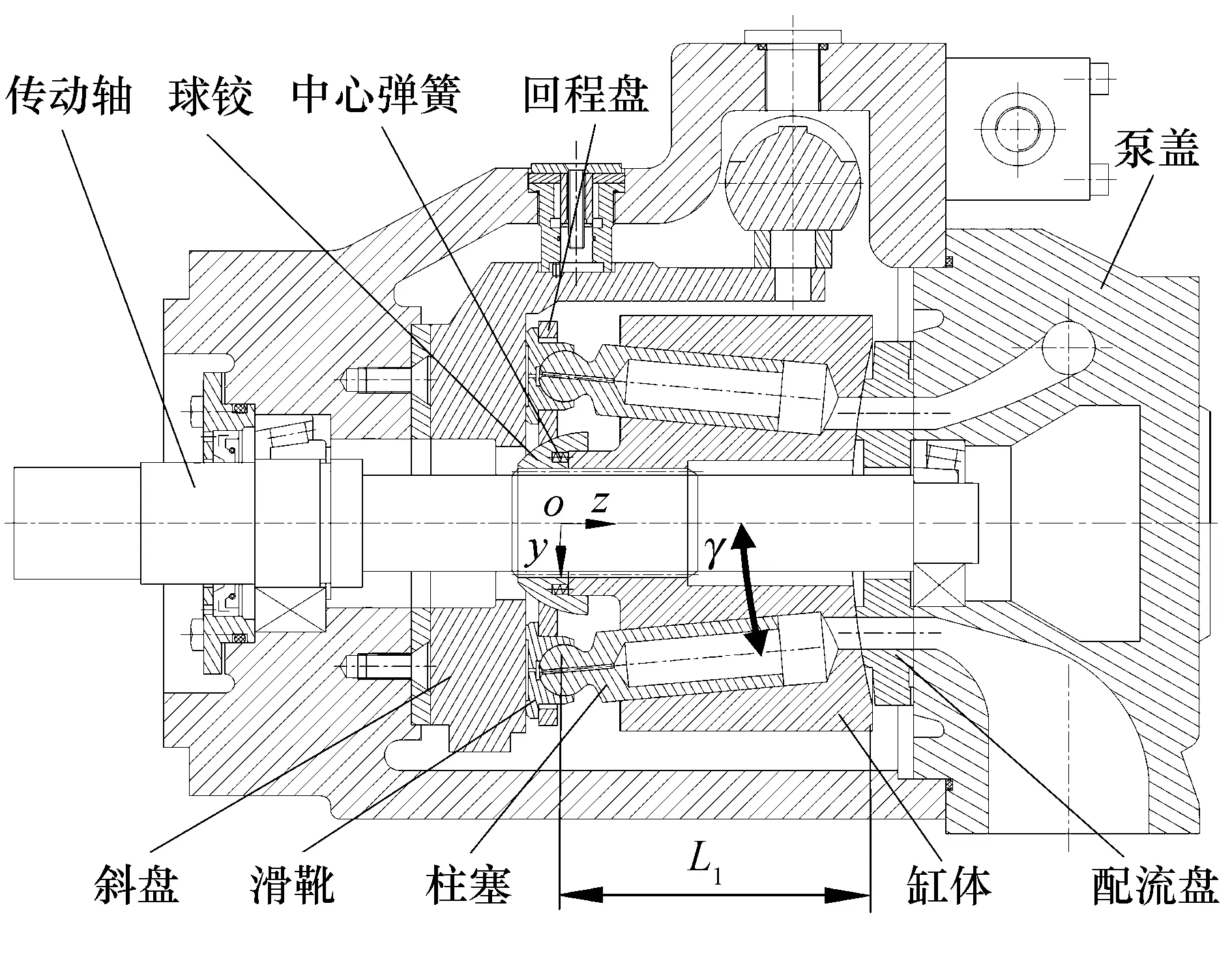
图1 斜盘式轴向柱塞泵结构简图Fig.1 Structural diagram of swash plate axial piston pump

图2为柱塞运动学分析示意图.图中绕y轴偏转的斜盘倾角为α，绕x轴偏转的斜盘交错角为β，缸体旋转角速度为ω，缸体旋转角度为φ.按右手系确定各符号的正负，即右手大拇指指向轴线的正方向，四指向心弯曲方向为偏转正方向，则图2中α、β和φ均为正.柱塞倾角为γ，坐标系原点o到配流盘配流表面的距离为L1，缸体配流端处柱塞孔分布圆半径为R.

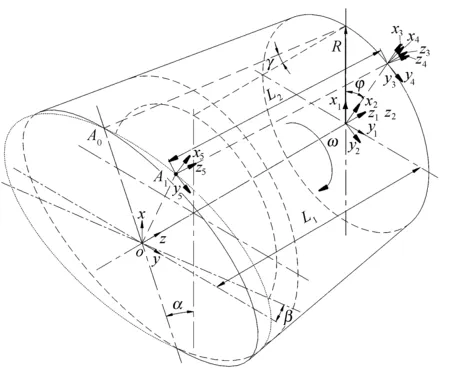
图2 柱塞运动学分析示意图Fig.2 Kinematic analysis diagram of piston

取一单柱塞为研究对象，其他柱塞运动规律与其相似，相邻柱塞间仅有大小为柱塞夹角的相位差.以所研究柱塞处于下死点时为初始位置.由图2可知，当缸体转过φ角后，柱塞球头球心由A0点运动到A1点，A1点到配流盘配流表面的距离为L2，利用坐标变换法，A1点的坐标可由坐标原点o点经过5次坐标系变换后得到，即坐标系xyz沿z轴正向平移L1得到坐标系x1y1z1，x1y1z1绕z1轴正向旋转φ角得到坐标系x2y2z2，x2y2z2沿x2正向平移R得到坐标系x3y3z3，x3y3z3绕y3逆向旋转γ得到坐标系x4y4z4，x4y4z4沿z4反向平移L2得到坐标系x5y5z5，x5y5z5的坐标原点即为A1点坐标.

各坐标变换矩阵分别为

最终变换矩阵为T05=T01T12T23T34T45,即

式中:M=L2cosφsinγ+Rcosφ

N=L2sinφsinγ+Rsinφ

由以上可得点A1的空间位置坐标：

(1)

各柱塞球头球心所在平面方程可由其法线方向得到，该法线方向同时与各柱塞球头球心所在平面和xoz平面、yoz平面交线的方向向量垂直，而两交线的方向向量由图3可得：

n1=(1,0,-tanα),n2=(0,-1,-tanβ)

则所求法线方向为两方向向量的叉积

-itanα+jtanβ-k

故各柱塞球头球心所在平面方程为

-xtanα+ytanβ-z=0

(2)

显然，A1点坐标必满足此方程，联立式(1,2)得

则缸体转过φ角后相应柱塞的位移为

(3)

对式(3)求导可分别得到柱塞的速度、加速度为

(4)

a={ω2(R+L1tanγ)·[sin 2φtanαtanβtanγ+

sinφtanβ-cosφtanα+

(tan2α+2tan2β)tanγcos2φ+

(tan2β+2tan2α)tanγsin2φ]}/

cosγ(1-tanαtanγcosφ+tanβtanγsinφ)3

(5)

式(3～5)为考虑斜盘有两个方向倾角和柱塞倾斜布置时单柱塞运动学分析的一般模型.

2 模型验证及分析

为验证模型的正确性，分下述几种情况讨论：

1)α≠0，β=γ=0

该情况为柱塞泵经典结构形式，即柱塞轴线与传动轴轴线平行，斜盘仅有一个方向的倾角.将β=γ=0代入式(3～5)得到柱塞的位移、速度和加速度分别为

该结果与文献[14]一致.

2)α≠0,γ≠0,β= 0.

该情况斜盘仅有一个方向的倾角，柱塞轴线与传动轴轴线的夹角为倾斜布置.将β= 0代入式(3～5)得到柱塞的位移、速度和加速度分别为

(9)

(10)

a2=-[ω2(R+L1tanγ)·(tanαcosφ-

tan2αtanγcos2φ-2tan2αtanγsin2φ)]/

cosγ(1-tanαtanγcosφ)3

(11)

该结果与文献[15]一致.分别以式(6～8)所对应位移、速度和加速度的最大值为参考值，对式(9～11)进行无量纲化，并画出柱塞倾角不同时柱塞的运动学曲线如图4所示.由图4可知，柱塞倾角越大，柱塞运动曲线离简谐运动规律越远，相应柱塞位移、速度及加速度的最大幅值变大，故加大柱塞倾角可增加柱塞泵的排量，柱塞沿其轴线方向的速度和加速度的增大会提高柱塞腔液流瞬时速度及柱塞的惯性力.

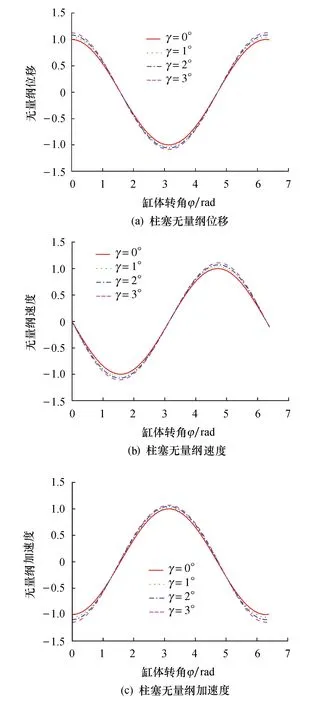
图4 不同柱塞倾角下柱塞运动学比较图

3)α≠0，β≠0，γ= 0

该情况斜盘有两个方向的倾角，柱塞轴线与传动轴轴线平行.将γ= 0代入式(3～5)得到柱塞的位移、速度和加速度分别为

d3=R(tanαcosφ-tanβsinφ)

(12)

v3=-ωR(tanαsinφ+tanβcosφ)

(13)

a3=-ω2R(tanαcosφ-tanβsinφ)

(14)

该结果与文献[12]一致，表明文献[13]结果有待商榷.同理对式(12～14)进行无量纲化，在斜盘倾角α一定时，可画出斜盘交错角β不同时柱塞的运动学曲线如图5所示.

比较式(6～8) 和式(12～14)及由图5可知，柱塞在斜盘两个方向上倾斜时的运动实质为柱塞在斜盘两个方向上分别倾斜时柱塞运动的线性叠加，两个分运动为频率相同相位相异的简谐运动，叠加后的运动仍为简谐运动.随着斜盘交错角变大，柱塞的位移、速度及加速度幅值亦增大.

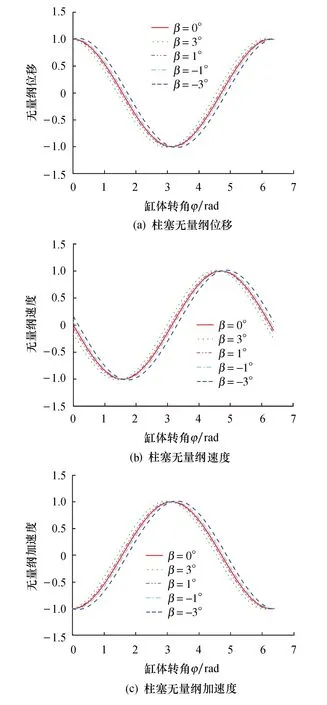
图5 不同斜盘交错角下柱塞运动学比较图

同时，由图4可知斜盘交错角结构使得柱塞运动上下死点发生变化，改变了柱塞腔配流过渡过程预压缩和预膨胀角，这将对柱塞腔压力瞬态过渡过程及瞬时流量特性产生影响.由上下死点位置处柱塞运动速度为零的特征，令式(13)为零,即v3=0，可找到上下死点偏转角与斜盘两个方向倾角间的关系为

(15)

通常斜盘交错角β设计加工后为一确定值，柱塞泵通过改变斜盘倾角α的大小来实现变量.由式(15)可画出不同斜盘交错角时上下死点偏转角随斜盘倾角改变时的变化规律,如图6所示.由图6可知:采用负的斜盘交错角时，上下死点偏转角偏转方向与缸体旋向相同为正，推迟柱塞腔预压缩和预膨胀过程，反之则为负，提前柱塞腔预压缩和预膨胀过程；在斜盘变量过程中，上下死点偏转角随斜盘倾角改变而变化，斜盘交错角绝对值越小，上下死点偏转角的变化梯度随斜盘倾角变小而增大，而当斜盘倾角在大排量范围内变化时上下死点偏转角的变化梯度变小；上下死点最大偏转角为90°，此时斜盘倾角为零.

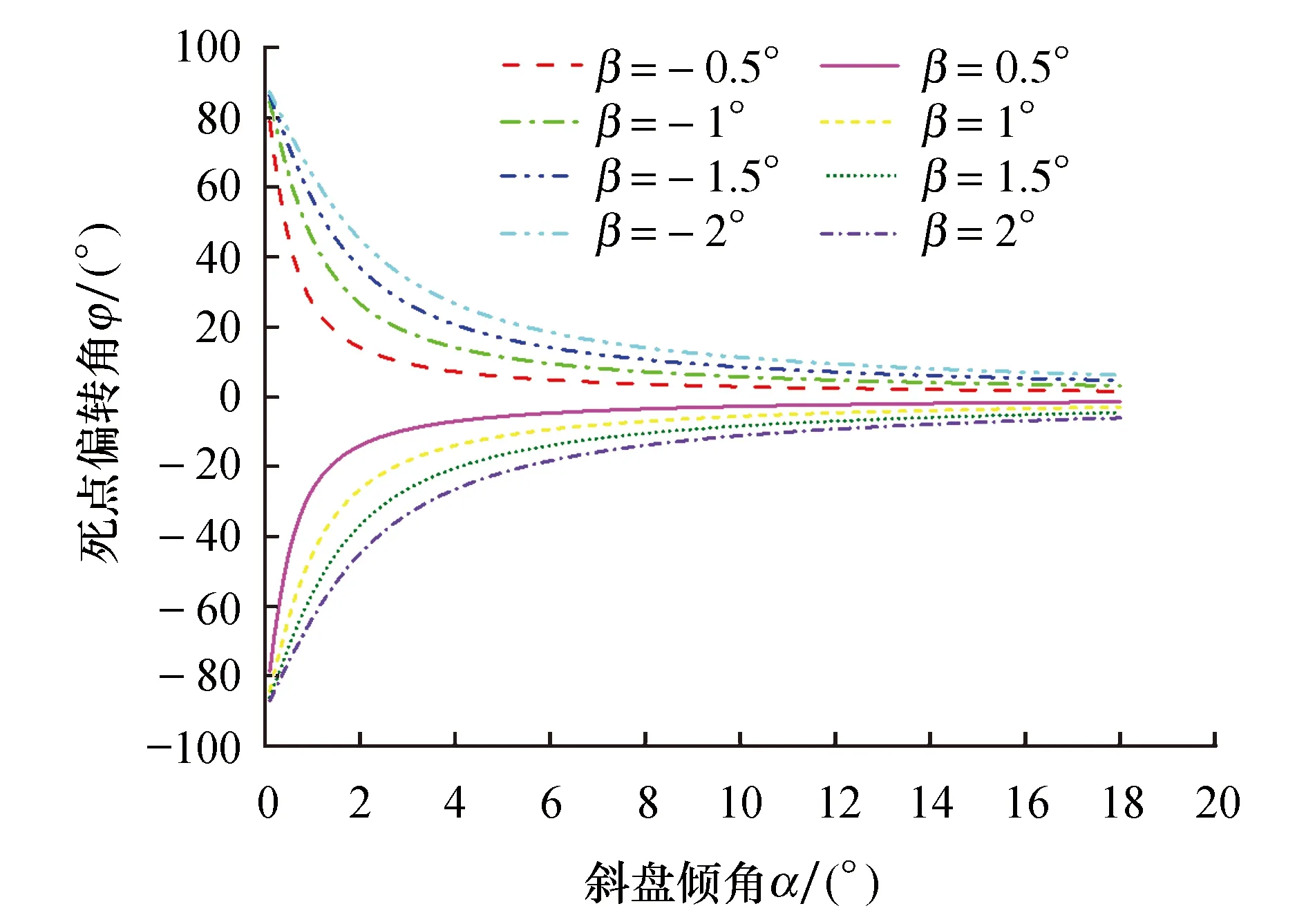
图6 变量过程不同斜盘交错角时上下死点偏转角变化规律Fig.6 Internal and external dead point transformation diagram with different cross angles under variable process

4)α≠0、β≠0、γ≠ 0

该情况为考虑斜盘两个方向有倾角且柱塞倾斜布置，具有潜在开发可能.此时可由式(3～5)对柱塞的运动学进行分析，同理可画出斜盘倾角一定，不同柱塞倾角和斜盘交错角时柱塞无量纲位移、速度和加速度曲线,如图7所示.由图7可知，斜盘交错角使柱塞运动的相位发生变化，柱塞倾角使柱塞运动曲线呈类简谐规律变化，斜盘交错角和柱塞倾角增大均会引起柱塞的位移、速度和加速度最大幅值增大.

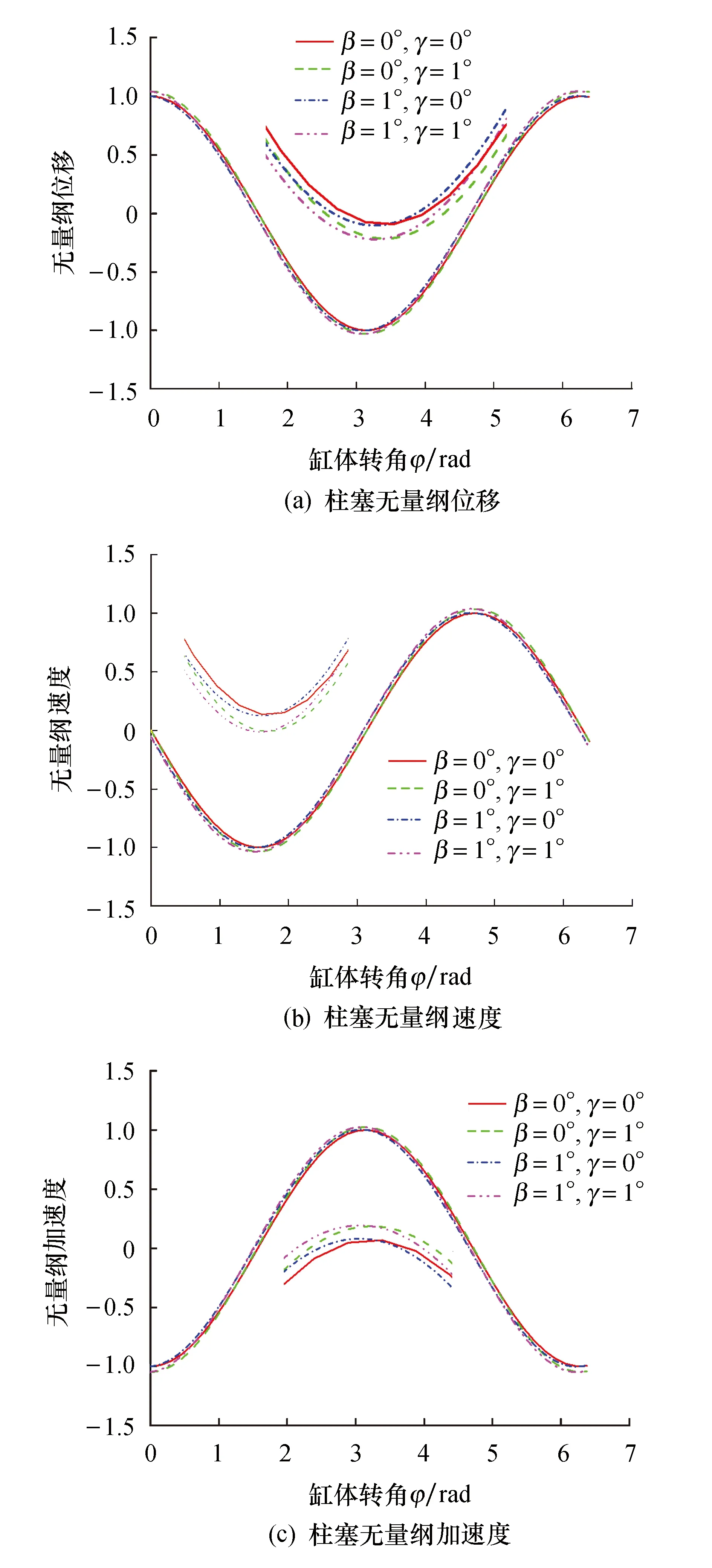
图7 不同斜盘交错角及柱塞倾角下柱塞运动学比较图Fig.7 Kinematic comparisons of piston with different swash plate cross angles and plunger inclination angles

3 结论

本文在同时考虑斜盘式轴向柱塞泵斜盘倾角、斜盘交错角及柱塞倾角结构特征的基础上，采用坐标变换法推导出了斜盘式轴向柱塞泵柱塞运动学分析的一般模型.经不同情况讨论及与已有文献对比分析，验证了该一般模型的正确性.对已有文献中关于斜盘有两个方向的倾角，柱塞轴线与传动轴轴线平行布置时柱塞运动学模型的不一致情况进行了澄清，可作为斜盘式轴向柱塞泵设计的理论基础.经对一般模型进行分析可总结出如下结论:

1) 斜盘交错角使柱塞运动的相位发生变化；柱塞倾角使柱塞运动曲线呈类简谐规律变化；斜盘交错角和柱塞倾角增大均会引起柱塞的位移、速度和加速度最大幅值增大，位移增大可增加柱塞泵的排量，柱塞沿其轴线方向的速度和加速度的增大会提高柱塞腔液流瞬时最大速度及柱塞的惯性力.

2) 按右手系惯例约定参考坐标系,判定各倾角正负号.采用负的斜盘交错角时，上下死点偏转角偏转方向与缸体旋向相同为正，推迟柱塞腔预压缩和预膨胀过程，反之则为负，提前柱塞腔预压缩和预膨胀过程；在斜盘变量过程中，上下死点偏转角随斜盘倾角改变而变化，斜盘交错角绝对值越小，上下死点偏转角的变化梯度随斜盘倾角变小而增大，而当斜盘倾角在大排量范围内变化时上下死点偏转角的变化梯度变小；上下死点最大偏转角为90°，此时斜盘倾角为零.