改进的基于身份的分层加密方案
贾王晶,郭丽峰,马添军
(1.山西警察学院 网络安全保卫系,山西 太原 030006;2.山西大学 计算机与信息技术学院,山西 太原 030006;3.中国科学院 信息工程研究所,北京 100093)
0 引言
基于身份的加密(Identity-Based Encryption,IBE)的概念是由Shamir[1]首先提出的,虽然之后国内外也有许多关于IBE方案的研究[2-3],但一直没有一个令人满意的实用的IBE方案。Boneh和Franklin[4-5]在2001年提出了一种基于身份的加密方案,该方案实用且能够抵抗随机预测模型下的密文攻击的自适应选择。IBE体制利用用户身份来生成公钥,这样就避免了分发公钥证书的步骤,极大减轻了可信第三方机构的管理负荷。但是IBE方案在大型网络上用户大量增多的情况下,单个私钥生成器(PKG)的运行效率成为应用的瓶颈。为了解决这个问题,在IBE的基础上,提出了基于身份的分层加密体制(Hierarchical Identity-Based Encryption,HIBE)。在HIBE方案中,低级别的PKG中的私钥由其上一层PKG生成,减轻了高级别PKG中的工作负担。HIBE的另一个优点是某一层PKG私钥的泄露不会影响更高层PKG的私钥安全性。Horwitz和Lynn[6]首次提出了HIBE体制。之后,Gentry和Silverberg[7]在随机预言模型下构建了一个安全的HIBE方案。Boneh 和Boyen[8]构建了一个在选择身份模型下安全的HIBE方案。Boyen和Waters[9]构建了一个匿名的HIBE方案。Gentry和Halevi[10]构建了一个完全安全的HIBE方案,但代价是困难性假设和密文大小会随着层深度增加而线性增加。
上述几个HIBE方案[7-10]的安全性证明都是采用分割策略,虽然已被证明可行,但它有两个限制:1)使用分割技术需要使用大量的公共参数去构建一个完全安全的方案;2)分割技术对于有更多功能需求的加密体制(如HIBE)的安全性证明已经不再适用。Waters[11]提出了双系统加密理论来证明IBE和HIBE方案的安全性,弥补了分割策略的不足。Lewko和Waters[12]成功地将双系统加密技术应用到了他们所构建的IBE和HIBE方案中的安全性证明中。Kwangsu Lee[13]利用双系统加密技术构建了一个可撤销的HIBE方案。Ramanna 和Sarkar[14]和Hoeteck Wee[15]利用双系统加密技术构建了匿名的HIBE方案。另外,王皓[16]、张敏情[17]、马海英[18]、杨其[19]、赵志远[20]、宋文纳[21]、陈丹伟[22],Langrehr[23]等都使用相似的方法构造出了属性基加密方案。
本文改进了Waters的HIBE方案[11],减少了其密钥生成时的参数,加快了密钥生成算法生成密钥的速度,提高了HIBE方案的运行效率,使得HIBE方案更加实用,并使用双系统加密证明技术证明了完全安全性。改进思路如下。
1)HIBE方案生成密钥时,是由上层用户生成下层用户的密钥,需要做两点工作:一是将新增Id嵌入到密钥中,二是要保证生成的密钥充分随机。在Waters的方案中,用于保证生成密钥充分随机化的参数过多,这样就导致算法效率降低,所以我们的工作在于减少密钥生成时的随机参数,加快方案密钥生成的时间,提高算法效率,同时又保证生成的密钥充分随机。下面将详细介绍密钥生成时的过程:
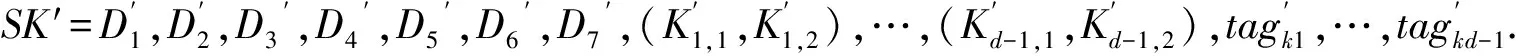
2)本方案的安全性证明依赖于双系统加密技术以及游戏序列的应用,如果我们可以利用困难性问题的参数构造得到每个游戏过程合理的半职能密文和半职能密钥,则我们可以使用双系统加密证明技术的证明思路来证明方案的安全性。
1 基础知识
1.1 双线性对
设G,G1是两个循环群, |G|=|G1|=p,p是素数,G=
1)双线性性:对于任意u,v∈G和a,b∈Z,都有:e(ua,vb)=e(u,v)ab;
2)非退化性:e(g,g)≠1;
3)可计算性:任意的u,v∈G都可以有效计算e(u,v);
4)对称性:对于任意的a,b∈Z,有e(ga,gb)=e(gb,ga).
1.2 困难性问题
判定双线性Diffie-Hellman问题(Decisional Bilinear Diffie-Hellman Problem,DBDH问题)
设G,G1是两个循环群, |G|=|G1|=p,其中p为素数,且G=
判定线性问题(Decisional Linear Problem,DLE问题)
G为p阶素数群,随机选择g,f,γ∈G,使其满足G=
2 双系统加密技术应用
2.1 正常密文/密钥与半职能密文/密钥的引入
密钥和密文在利用双系统加密技术的证明策略中被分为正常的和半职能的,它们又分别对应两种密钥和密文生成算法:一种是在实际方案中使用的正常密钥和正常密文生成算法;另一种是在安全性证明时使用的半职能密钥和半职能密文生成算法。它们之间的关系如下图1所示。
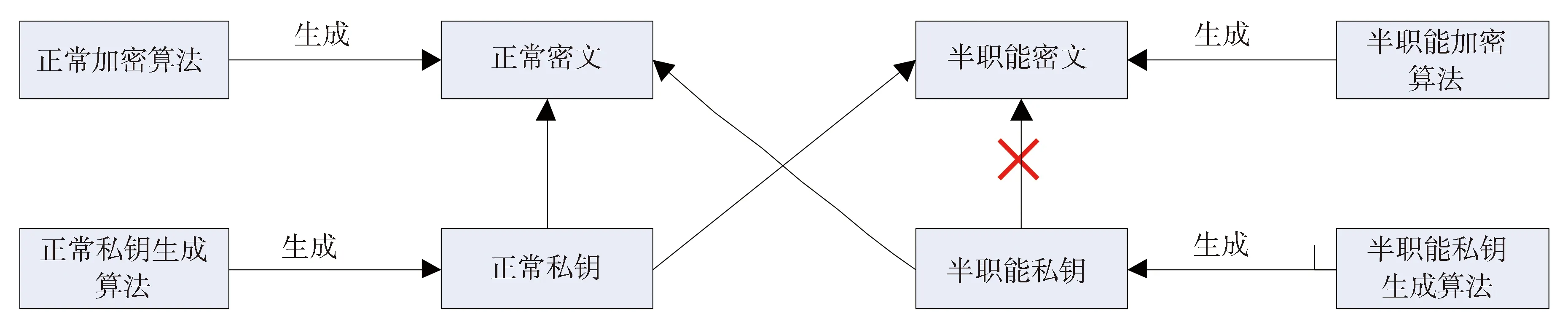
Fig.1 Relationships between normal and semi-functional ciphertexts/keys图1 正常与半职能密文/密钥的关系
2.2 双系统加密技术的证明策略及安全游戏的定义
为了证明方案的安全性,Waters定义了一系列的安全性游戏。分别有以下几种:
GameReal:是真实的HIBE安全性游戏[7]。
Gamei:与GameReal的区别在于:1)对敌手回复的是半职能的挑战密文;2)当敌手向挑战者发送的私钥询问次数k≤i时,发送给敌手的是半职能密钥,否则是正常密钥。
若敌手询问了q次私钥,那么有Game0,Game1,…,Gameq共q+1个游戏。在Game0与Gameq中,挑战密文都是半职能的,密钥分别是正常的和半职能的。
GameFinal:与GameReal的区别在于:1)将通过半职能密文生成算法加密得到的半职能密文当作挑战密文;2)所有询问的密钥都是半职能的。
方案安全性证明的总体证明步骤如下:1)证明GameReal和Game0的不可区分性;2)证明游戏Game0,Game1,…,Gameq中任意两个相邻的游戏Gamek-1和Gamek的不可区分性,注意选择的游戏要满足1≤k≤q;3)证明Gameq和GameFinal的不可区分性,如下图2所示。由于敌手在游戏GameFinal中的优势为0,所以只要能够证明这些游戏之间的不可区分性,就可以证明方案的安全性。
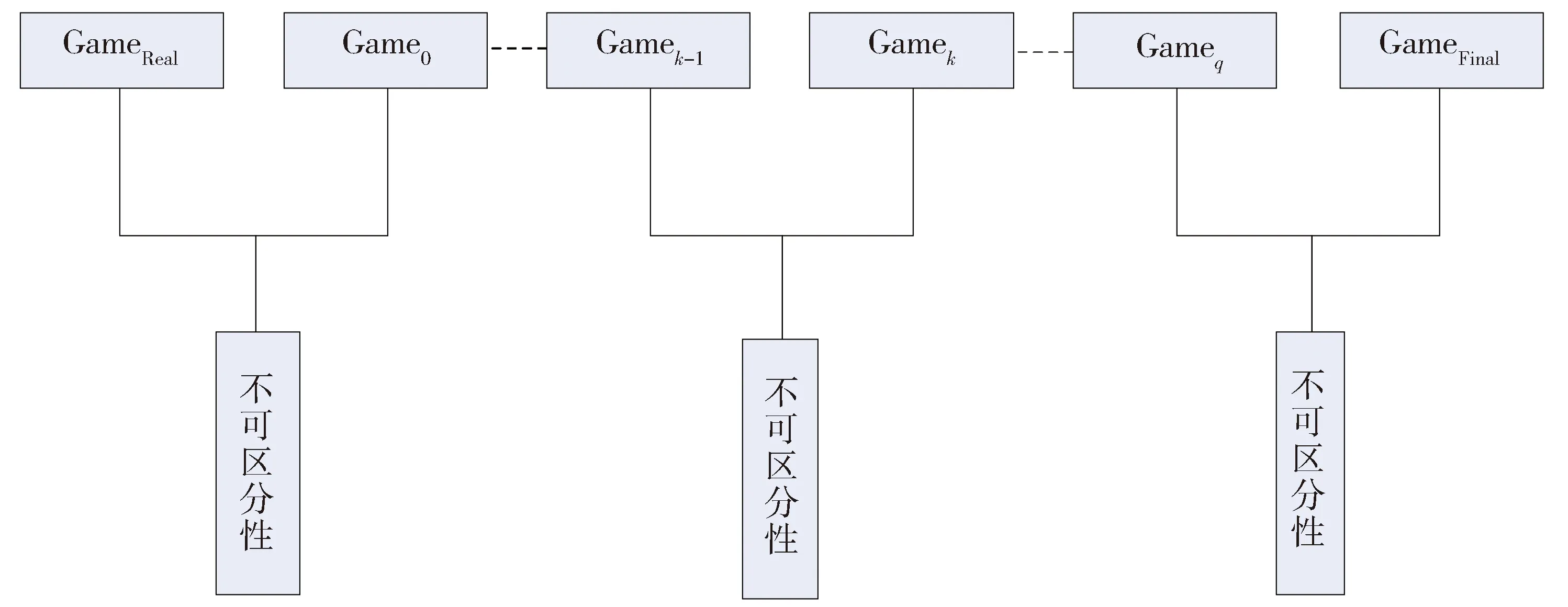
Fig.2 Partition of the game图2 游戏划分
2.3 双系统加密技术的矛盾问题
矛盾问题:模拟者无需借助敌手就可以区分游戏Gamek-1和Gamek,即使用用户身份对应的私钥来解密当前身份的半职能密文,若能正确解密,则是正常密钥,若不能正确解密,则为半职能密钥。为了解决这个矛盾,方案设计中引入tag,从而使得模拟者也无法区分正常密钥和半职能密钥。
3 改进的HIBE方案
3.1 改进HIBE方案的构造
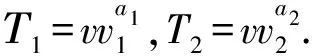
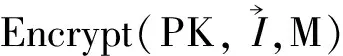
C1=(gb)s1+s2,C2=(gba1)s1,C3=(ga1)s1,C4=(gba2)s2,
E1=(u1I1wtagc1h1)t,…,Ed=(udIdwtagcdhd)t,E=gt.
生成密文CT=C0,…,C7,E1,…,Ed,E,tagc1,…,tagcd.
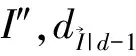
当d=1时,随机选择μ1,tagk1,r2,z1,z2∈Zp,令r1=μ1,r=r1+r2.之后计算身份I″对应PKG的私钥。
D7=gr1,(K1,1=(u1I1wtagk1h1)μ1,K1,2=gμ1) ,
所以,dI″|1.
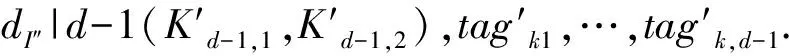
……
为给第d层生成私钥,上一层第d-1层的PKG随机选择μd,tagkd∈Zp,计算tagk1,…,tagk,d-1.
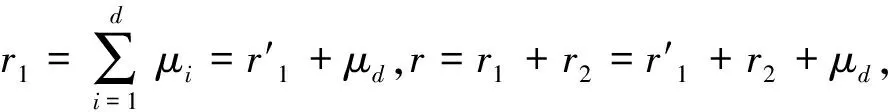
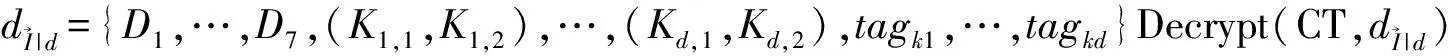
在解密之前,我们先做一系列的计算。首先,计算:
A1=e(C1,D1)·e(C2,D2)·e(C3,D3)·e(C4,D4)·e(C5,D5)=
e(g,g)αa1bs2·e(v,g)b(s1+s2)r·e(v1,g)a1bs1r·e(v2,g)a2bs2r.
接着,计算:
A2=e(C6,D6)·e(C7,D7)=e(v,g)b(s1+s2)r·
e(v1,g)a1bs1r·e(v2,g)a2bs2r·e(g,w)-r1t,
A3=A1/A2=e(g,g)αa1bs2·e(g,w)r1t.
如果tagc≠tagk,则解密算法计算:
A4=(e(E1,K1,2)/e(E,K1,1))1/(tagc1-tagk1)…
则最后,我们可以恢复出明文,通过如下计算:C0/(A3/A4)=M.
3.2 半职能算法
我们首先来介绍改进的HIBE体制中半职能密文和半职能密钥的生成算法。半职能密文和半职能密钥由主密钥、正常密钥和正常密文生成。但请注意,在实际系统中,不使用半功能密钥和半功能密文,其主要目的是用于安全证明。
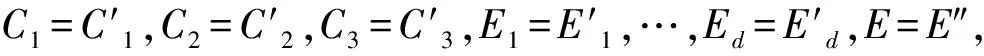
最后得到的半职能密文为CT=C0,…,C7,E1,…,Ed,E,tagc1,…,tagcd.
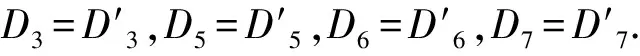
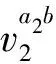
3.3 安全性证明
改进方案的安全性证明中的游戏划分以及证明策略等,与使用双系统加密技术的证明过程基本相同。
引理1 假设存在算法A,区分GameReal和Game0的优势概率为:GameRealAdvA-Game0AdvA=ε,则我们可以构建一个算法B,以优势GameRealAdvA-Game0AdvA=ε解决DLE问题。
证明算法B输入参数(G,g,f,γ,gc1,fc2,T),输出结果若为0,则T=γ(c1+c2),输出结果若为1,则相反。接着描述算法B的模拟过程。
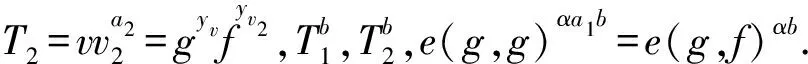
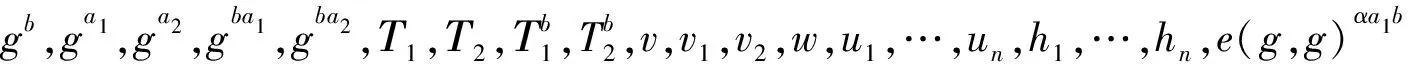
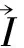
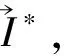
最后将CT=C0,…,C7,E1,…,Ed,E,tagc1,…,tagcd发送给敌手A。
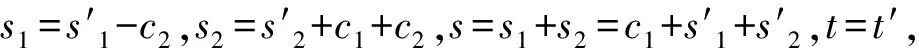
猜测阶段:A输出对β的猜测β′∈{0,1}。若β=β′,B输出0。从上述证明过程可以看出,若T=γ(c1+c2),则算法B模拟的是GameReal,否则模拟的是Game0。到目前为止,算法B成功模拟了GameReal或Game0,若敌手A区分GameReal和Game0的优势为ε,那么我们就认为算法B能够以优势ε解决DLE问题。
引理2 假设算法A区分Gamek-1和Gamek(1≤k≤q)的优势概率为:Gamek-1AdvA-GamekAdvA=ε,则我们可以构建一个算法B,以优势ε解决DLE问题。
证明算法B输入参数(G,g,f,γ,gc1,fc2,T),输出0表示T=γ(c1+c2),输出1表示T是G中任意元素。接着描述算法B的模拟过程。
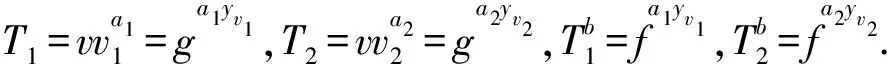
最后,算法B随机选择(A1,B1),…,(An,Bn)∈Zp,其中Ai,Bi∈Zp(1≤i≤n)之后设置:
w=fgyw,u1=f-A1gyu1,…,un=f-Angyun,h1=f-B1gyh1,hn=f-Bngyhn.
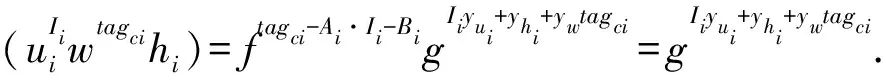
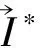
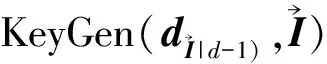
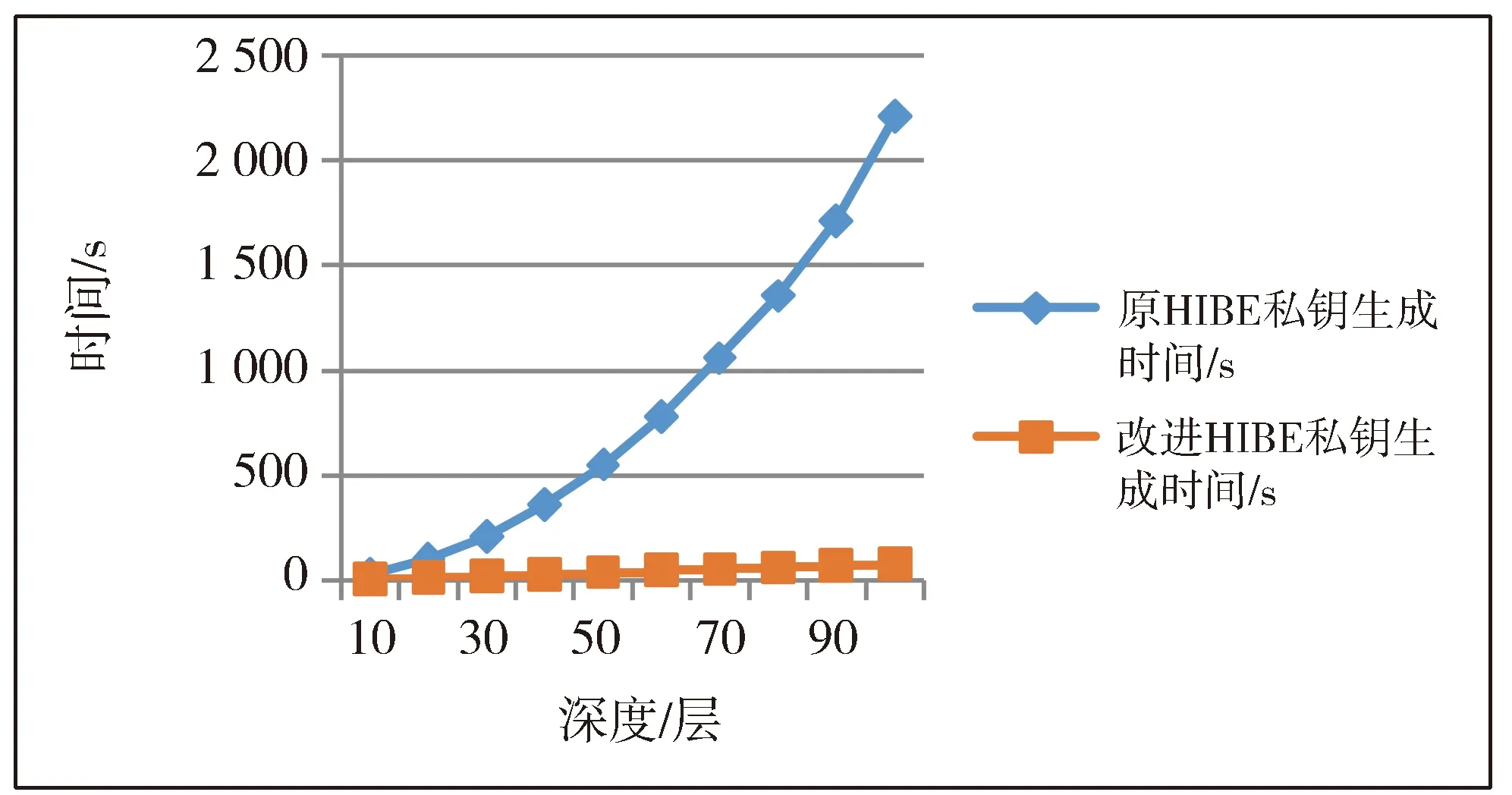
2)i … 猜测阶段:A输出对β的猜测β′∈{0,1}。 若β=β′,B输出0。从上述证明过程可以看出,若T=γ(c1+c2),则算法B模拟的是Gamek-1,否则模拟的是Gamek。到此为止,算法B成功模拟了Gamek-1或Gamek,若敌手A区分Gamek-1和Gamek的优势为ε,那么算法B能以优势ε解决DLE问题。 引理3 假设存在一个至多发出q次询问的算法A,区分Gameq和GameFinal的优势概率为:GameqAdvA-GameFinalAdvA=ε,则我们可以构建一个算法B,以优势ε解决DBDH问题。 证明算法B输入参数(g,gc1,gc2,gc3,T),若输出0表示T=e(g,g)c1c2c3,输出1表示T是G中任意元素。接着描述算法B的模拟过程。 初始化阶段:算法B输入安全参数λ和最大深度n,然后选择随机幂指数a1,b,yv,yv1,yv2,yw,yu1,…,yun,yh1,…,yhn,α∈Zp,接着设置如下参数: g=g,gb,ga1,ga2=gc2,gba1,gba2=(gc2)a2, v=gyv,v1=gyv1,v2=gyv2,w=gyw, u1=gyu1,…,un=gyun,h1=gyh1,…, hn=gyhn,e(g,g)α·a1·b=e(gc1,gc2)αa1. D5=(gb)-z2,D6=gbr2,D7=gr1, (Kd,1=(udIdwtagkdhd)μd,Kd,2=gμd) . C0=Mβ·Ta1b,C1=(gb)s1·(gc3)b,C2=(gb·a1)s1, C3=(ga1)s1,C4=(gc2)x′b,C5=(gc2)x′, 使s2=c3,x=x′-c3,当T=e(g,g)c1c2c3时,挑战密文是加密后的Mβ.否则,挑战密文是个随机消息。 猜测阶段:A输出对β的猜测β′∈{0,1}. 若β=β′,B输出0。从上述证明过程可以看出,若T=e(g,g)c1c2c3,则算法B模拟的是Gameq,否则模拟的是GameFinal.到目前为止,算法B成功模拟了Gameq或GameFinal,如果敌手A能够以优势ε将Gameq和GameFinal区分开来,则我们说算法B以概率为ε的优势解决了DBDH问题。 定理1 如果DLE问题和DBDH问题是困难的,则不存在多项式时间内的算法可以攻破本文所提出的HIBE方案。 证明由于对于任何敌手,其在GameFinal中的优势为0,而根据引理1,2,3可知,GameReal和GameFinal是无法区分的,因此其在GameReal中的优势也为0,定理得证。 在调用KeyGen算法为深度为d的身份向量生成私钥时,原HIBE方案每一层都需要2d+3个参数,d层共需要d(2d+3)个参数。而改进HIBE方案生成第一层私钥需要3个参数,其余每层只需要两个参数,因此d层共需要2d+3个参数。由下表1中(n代表最大深度,d代表身份向量深度)可见改进HIBE方案相对而言在私钥生成阶段所需参数较少。 表1 HIBE和改进HIBE方案的参数对比 表2中,描述的是原HIBE与改进HIBE的私钥生成时间。图3是根据表2中的数据所作出的时间对比图,从图中可以看出,改进HIBE的效率要高。 表2 原HIBE与改进HIBE私钥生成时间 Fig.3 Comparison of private key generation time between two schemes图3 两种方案的私钥生成时间对比 本文改进了Waters构建的HIBE方案,并构建了与原始方案相比具有更优化的密钥参数和效率,且在标准模型下是完全安全的改进的HIBE方案。但目前这个方案只是对私钥生成算法方面的改进,因此如何在简单困难性假设下构建一个参数更少,效率更高且完全安全的HIBE方案,仍然是一个非常值得研究的问题。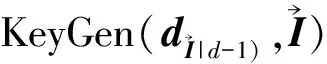
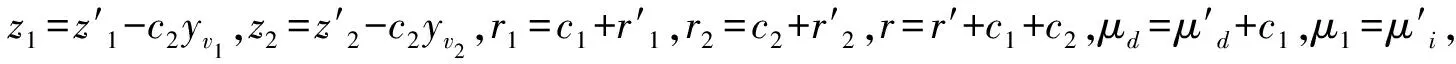
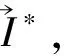
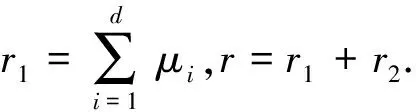
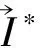
3.4 效率比较


4 结论与展望

