建筑外立面构件对室内自然通风效率的影响
崔冬瑾,赵祥路,袁 磊,钟鸿峰
1)深圳大学建筑与城市规划学院,广东深圳 518060;2)深圳市建筑环境优化设计研究重点实验室,广东深圳 518060
近年来,自然通风作为实现建筑节能的重要途径之一,得到人们的广泛关注和采纳[1-2]. 在绿色建筑设计中,常采用外立面构件以提升建筑自然通风性能,营造节能舒适的室内环境. 实地调研发现,在高密度城市中,集约型的居住空间配置模式使得单侧通风变得越来越普遍. 目前,已经有很多研究者对建筑单侧自然通风情况开展了较充分的研究工作[3-7].NIU等[5]研究表明,在室内和室外温差达3~5 ℃,且风速高于0.9 m/s的条件下,风压通风将取代热压通风成为自然通风的主要驱动力;AI等[6]关于城市风环境的研究显示,周边扰流建筑会显著降低目标建筑的通风换气效率; ZHU等[8-11]指出在周边扰流建筑中,上游扰流建筑会大幅度降低大气来流风速;ASHRAE[12]研究发现,上游建筑的尺寸,尤其是上游建筑高度,直接决定了建筑背风面涡流区的大小. 然而目前的研究大多关注平滑立面的单栋建筑的通风情况,关于周边扰流建筑和外立面构件影响下室内自然通风效果的研究相对较少.本研究基于计算流体力学(computation fluid dynamics, CFD)数值模拟,研究在两种不同的来流风向(来流风向和建筑外窗法线的夹角α分别是 0°和45°)作用下,上游扰流建筑和外立面遮阳构件对目标建筑室内自然通风效率的影响. 上游扰流建筑被赋予了不同的高度比值,分别是等同于下游目标建筑,或是下游目标建筑高度的两倍.同时,外立面遮阳构件也具有垂直和水平两种类型. 根据控制变量法,分别对来流风向角度、上游扰流建筑高度比以及外立面遮阳构件的类型3个主要影响因素进行分析.
1 计算方法和模型验证
1.1 风洞实验介绍
本研究选取ZHANG等[13]的风洞实验结果用于CFD模拟的验证. 该风洞实验研究了扰流建筑对住宅建筑立面上的风压分布的影响,测试段长为14 m,横截面积为3.0 m×2.0 m,如图1所示. 实验中下游目标建筑物(实线)和上游扰流建筑物(虚线)的长宽高尺寸为0.1 m × 0.1 m × 0.6 m.

图1 建筑物相对位置的示意Fig.1 Schematic diagram showing relative location of buildings
ZHANG等[13]在风洞实验中测量了下游目标建筑物的墙壁S和N沿中心线的压力系数,无量纲数压力系数(Cp)为
Cp=(p-pr)/(0.5ρv2)
(1)
其中,p是测得的表面压力;pr是参考压力;ρ是大气密度. 在实验中大气密度为1.225 kg/m3;v是屋顶高度处的平均风速.标准k-ε模型和重整化群(re-normalization group, RNG)k-ε模型产生的Cp值的平均偏差,在迎风面分别为28.57%和6.21%,在背风面分别为-12.08% 和 -19.19%. 显然,RNGk-ε模型结果与风洞实验结果有更好的拟合性. CHANG等[9]研究单侧通风的立方体建筑室内和周围的流场特征,测量了建筑垂直中心平面内10条垂直线上的平均风速. AI等[7]运用CFD模拟估算了这些垂直线上的平均风速,模拟结果与测量结果吻合较好.
综合风洞实验和CFD模拟的结果比对,可以认为RNGk-ε模型能较好地反映建筑室内和周围的流场特征.
1.2 几何模型和案例设置
采用计算流体动力学方法,模拟了两种不同高度比的上游扰流建筑和两种不同类型的外立面构件对多层建筑的室内空气流动特性和空气质量的影响. 表1展示了18个不同的测试案例,以4层建筑为目标研究对象,模拟了在两种不同的来流风向下(来流风向和建筑外窗法线的夹角α分别是0° 和45°),有或没有垂直或水平翼墙,以及有或没有两种不同高度比的上游扰流建筑,对下游目标建筑室内自然通风效果的影响.
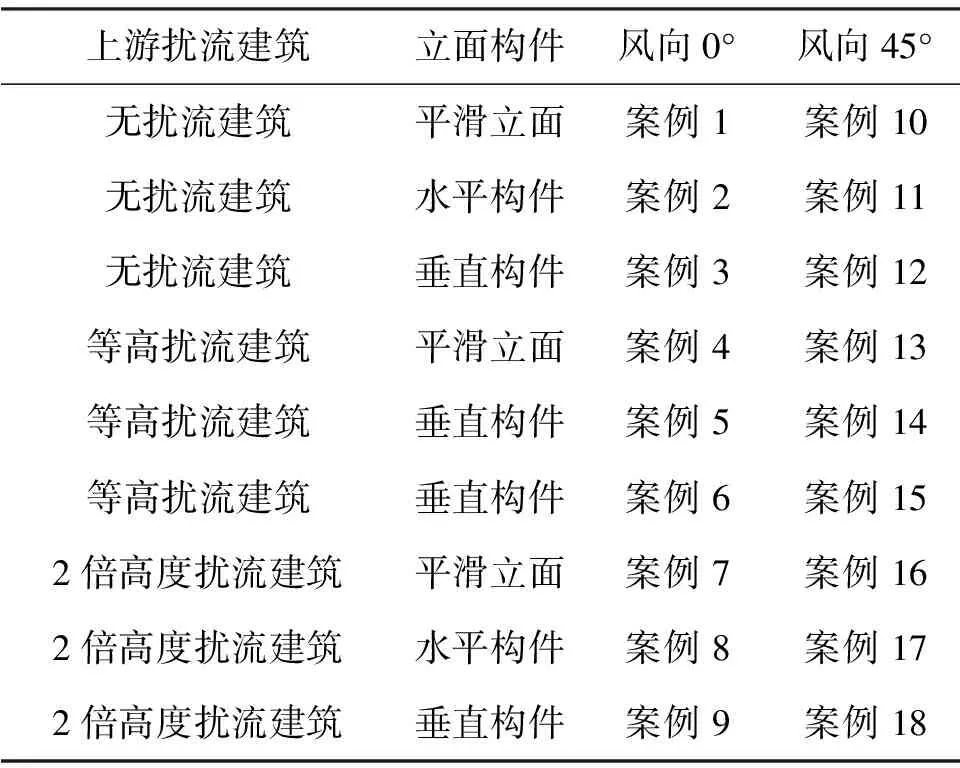
表1 案例1至18设置
图2展示了假设目标建筑的计算区域和几何模型,图2(a)采用了入口边界距离5Dy, 出口边界距离15Dy, 两侧距离7Dy, 高度10Dy的计算区域用于数值模拟计算. 根据LIU等[14]提出的最佳操作指南,此计算区域足够大,以减少边界对建筑物周围空气流动的影响. 两个不同高度比的上游扰流建筑(高度为Dz或2Dz)与目标研究建筑的距离为Dy.
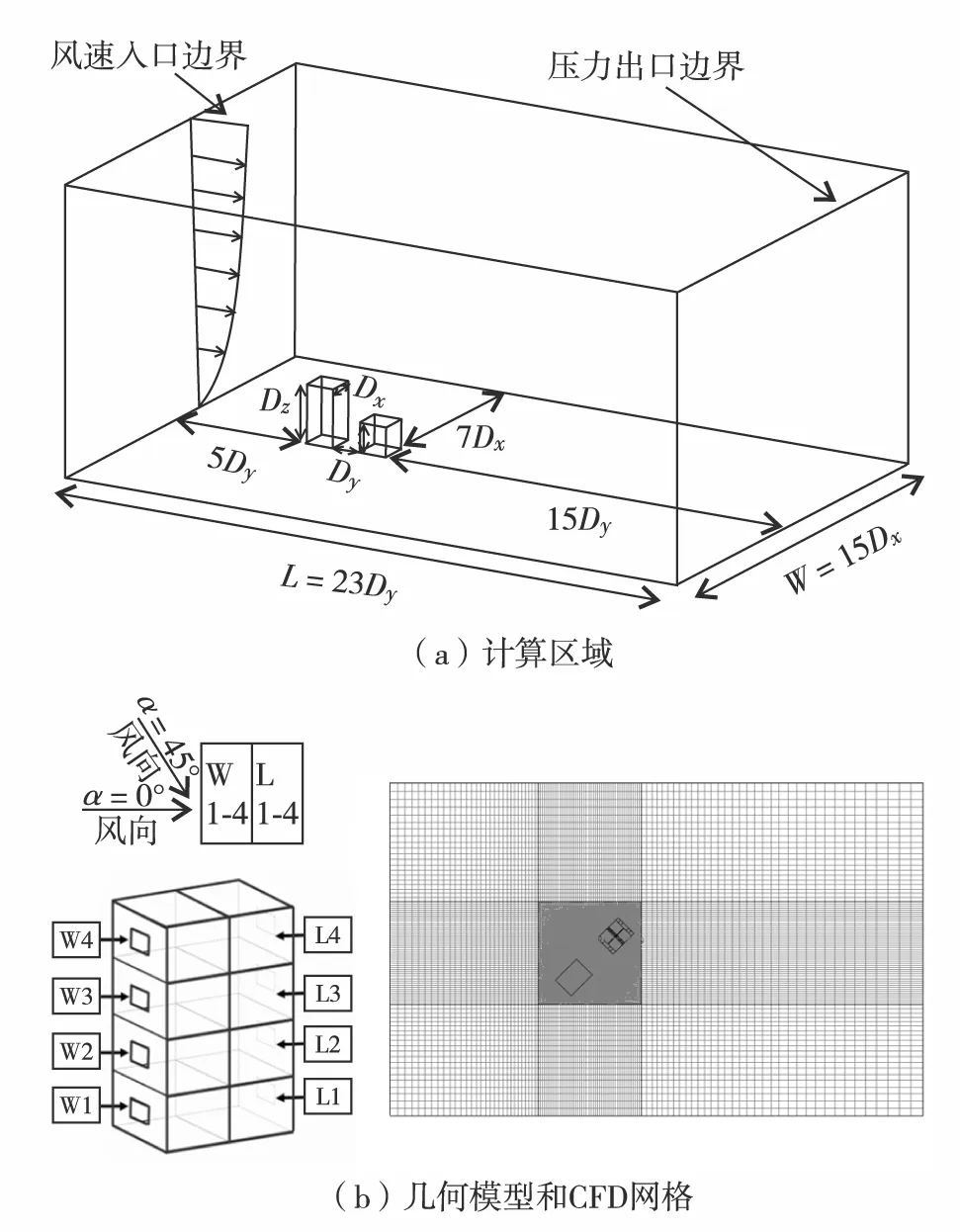
图2 计算区域和假设目标建筑模型Fig.2 Computational domain and building configurations
图2(b)显示了两种不同的来流风向,其中,α是来流风向与建筑物迎风侧的表面法线方向之间的夹角. 本研究对象是每层有两个独立房间的1∶20的4层建筑,1个房间在迎风侧有1个开口,而另1个房间在背风侧有1个开口. 目标建筑中每个房间的尺寸均为6 m × 3 m × 3 m,每个开口的尺寸固定为1 m × 2 m,开口高度为楼板高度以上1 m, 水平立面构件的尺寸为1 m×2 m,垂直立面构件的尺寸为1 m×1 m,目标建筑的长宽高尺寸为6 m×6 m×12 m(以上尺寸均为原型尺寸).
1.3 湍流模型和边界条件
本研究应用改进的非标准k-ε湍流模型,其在精度和计算的时间成本之间有较好的平衡[13-14].不可压缩流体的控制方程为
(2)
其中,u是速度矢量;φ是速度分量; Гφ是每个因变量φ的扩散系数;Sφ是源项;t是时间.
标准k-ε模型是基于湍流动能(k)及其耗散率(ε)的模型方程的半经验模型,湍流黏度μt为
(3)
其中,k是湍流动能(单位:m2/s2);ε是湍流耗散(单位:m2/s3)率;ρ是流体密度(单位:kg/m3);Cμ是模型常数,取0.085. 在标准k-ε模型的推导中,假设流动是完全湍流的,并且分子黏度的影响可以忽略不计[14], RNGk-ε模型提供了比标准k-ε模型更精确的流场模拟,部分原因是Rε增加了ε方程,这提高了涡流的精度,在ε方程中,增加了Rε项,
(4)
其中,η=Sk/ε,η0和β分别为4.38和0.015.
为了使得从缩尺模型的模拟研究中得到的定量数据,能够准确反映对应的原型建筑中的室内流场,必须在模型和原型之间满足一系列相似性准则.LIU等[14-15]研究表明,几何相似和边界层流相似是模型缩放时相对容易实现的. 本研究中,建筑物屋顶高度的风速为4 m/s,雷诺数约为4×104,远大于标准,因此可以满足雷诺独立性. 根据雷诺数相似法,对于忽略热效应,由适当的特征长度和参考速度实现的相似边界条件的流动系统,湍流是相似的.
网格精度测试基于无外立面构件的缩尺建筑模型,分别建立了网格数为210万、420万和650万个的有限元网格案例,分别代表粗糙、适中和高密度的不同网格方案. 以目标建筑室内每小时的换气次数(ACH)为参数评估网格的独立性,得出不同精度的网格对应的迎风面房间平均ACH值分别为17.0、16.0和16.2次/h,中间网格预测的ACH值非常接近于由更细网格预测的结果,偏差小于3%. 这一结果表明,采用420万的有限元网格用于后续的模拟计算相对合适.
关于边界条件的设置,入口边界以湍流强度和尺度为特征,分别为8%和1 m,湍流现象采用RNGk-ε模型,边界条件及参数设置依据操作指南[14]. 当使用标准壁函数时,近壁面y+值应在30~300. 在此研究模拟中,建筑物表面和计算区域地面附近的y+值均在30~40. 在流体均质不可压缩的假定下,质量流入口条件可以使用速度入口条件[15],为
Vz=VrefV(H/Dz)α=1.14Vrefz0.25
(5)
整个自然通风模拟计算区域中,出口边界采用压力出口条件,区域侧面和顶部采用对称边界,地面使用无滑移固壁边界条件,采用壁面函数并引入粗糙壁面修正设置,建筑物外立面使用无滑移墙面边界条件并采用标准壁面函数,但不引入粗糙壁面修正设置. 压力-速度耦合算法采用 SIMPLEC 算法,压力插值是二阶迎风,二阶离散化方案用于控制方程的对流和黏性项. 当所有缩放的残差平稳并且降到1×10-6以下,进出口质量相对误差为 0.003%,静压值在很小范围内周期性变化时,可以认为计算达到收敛.
2 模拟结果及分析
2.1 流场特征和通风性能
2.1.1 上游扰流建筑的影响
图3为来流风向为0°且无外立面构件的多层建筑室内和周围流场的风速等值线矢量图. 在风工程领域,建筑周围的风场流动模式已有广泛研究,对于单栋的单层或多层建筑,大气来流风向将在建筑2/3高度处产生分离,分别形成向上、向下和水平的流动, 这一现象与图3(a)显示的结果吻合.如图3(b)所示,等高度比的上游扰流建筑的存在,使下游目标建筑的迎风侧成为一个由向下流动的气流主导的流场,建筑顶部周围向上流动的气流消失了. 如图3(c)所示,两倍高度比的上游扰流建筑的存在,也改变了下游目标建筑迎风侧和背风侧的近壁面气流形式. 由以上分析发现,上游扰流建筑对下游目标建筑周围流场特性存在显著影响.
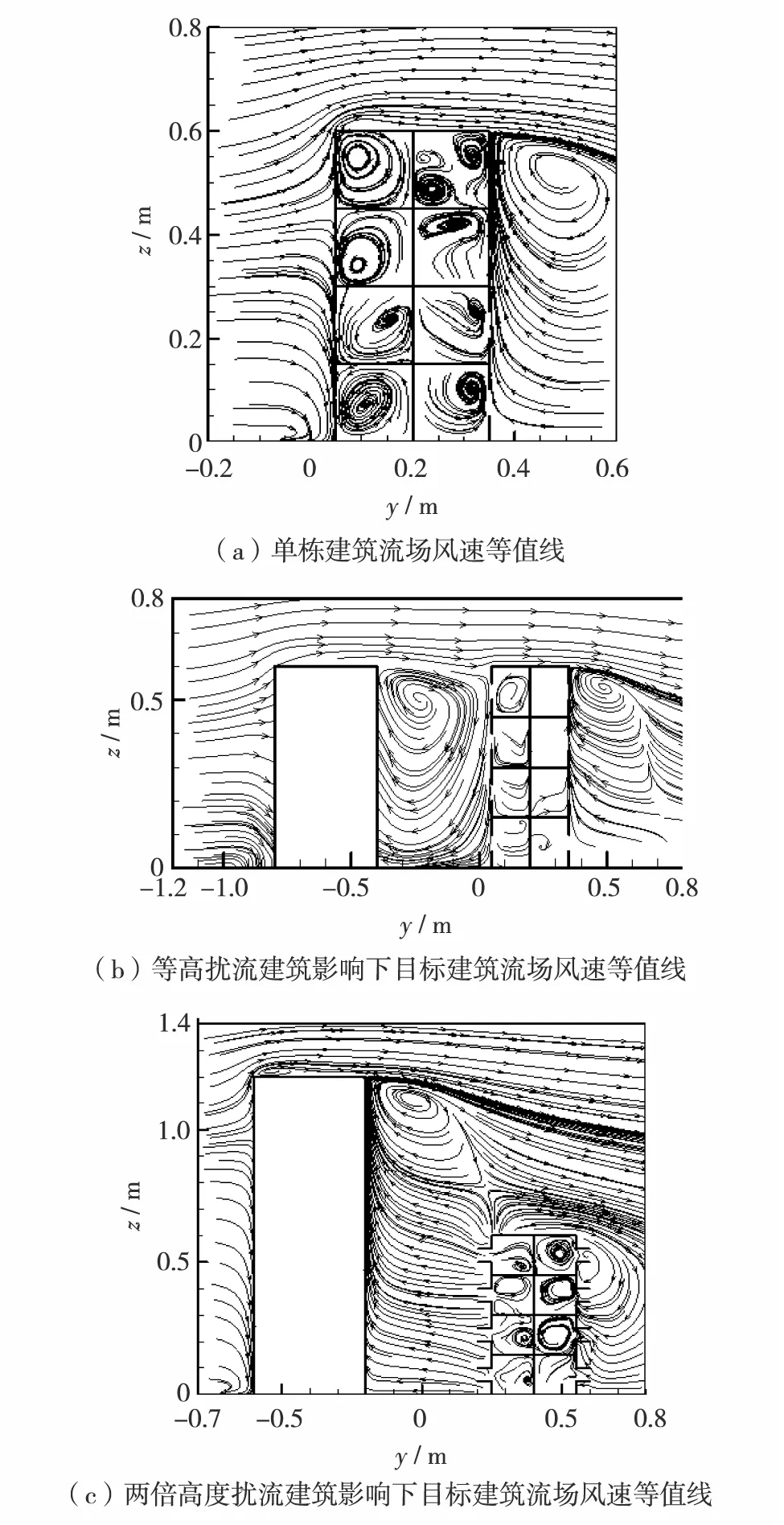
图3 上游扰流建筑影响下的风速等值线Fig.3 Contour of mean velocity magnitude of upstream turbulence buildings
2.1.2 外立面构件的影响
图4展示相同来流风向和上游扰流建筑的情况下,外立面构件对建筑室内和周边流场空气流动特性的影响. 如图4(a)所示,突出的垂直外立面构件给建筑近壁面的空气流动增加了阻力,加剧了湍流的波动,并增强了近壁面流体和立面构件的相互作用. 如图4(b)所示,在水平立面构件的角部出现了细微的涡流. 对比平滑壁面流场,立面构件的存在使得建筑近壁面形成了更动态的流场,成为了室内外空气交换的驱动力.
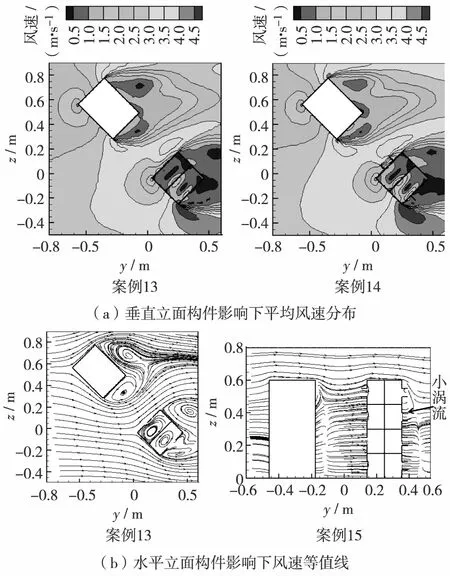
图4 立面构件周围流场Fig.4 Airflow around wing walls
2.1.3 上游扰流建筑和外立面构件的共同作用
图5展示了有等高度上游扰流建筑的情况下,建筑水平和垂直立面构件对流场的影响. 同样地,立面构件的存在干扰了近壁面气流模式,产生了很多小涡流,这种由立面构件产生的流场特征,不因上游扰流建筑的存在与否而改变. 但当有等高度比值的上游扰流建筑存在时,目标建筑周围流场的特征发生了改变. 此时,立面构件反而可能成为阻碍室内外空气交换的屏障,这意味着立面构件对建筑室内自然通风效率的作用效果受到上游扰流建筑的影响.

图5 立面构件影响下的风速等值线图Fig.5 Contour of velocity magnitude of envelope features
2.2 ACH值的对比分析
2.2.1 大气来流风向的影响
从图6中可以看出,对于在α= 45°的来流风向下的所有案例(即案例10—案例18),每小时换气次数(ACH)与α=0°的来流风向下的所有案例(即案例1—案例9)相比,增加了2~5倍. 其中, ACH使用面积积分方法计算为
(6)
其中,A为开口面积;U为风速. 式(6)表明,当来流风向与建筑物表面法线方向成一定角度时,目标研究建筑通常具有更好的自然通风性能.
2.2.2 外立面构件和上游扰流建筑的影响
通过比较垂直外立面构件的作用下不同案例中ACH的变化,可以看出,在迎风侧和背风侧,案例2和案例14的平均ACH分别大于案例1和案例13的平均ACH. 但是案例8和案例11的平均ACH仅在迎风侧分别大于案例7和案例10,案例5和案例17的平均ACH甚至分别小于案例4和案例16的平均ACH. 这表明垂直外立面构件对建筑室内自然通风效率的影响,很大程度上依赖于环境因素,包括近壁面的风向. 目标研究建筑的方位和朝向以及上游扰流建筑的高度比,对于水平外立面构件,在所有案例中,平均ACH均没有显著增加,并且在一些案例中,水平外立面构件甚至对室内自然通风效果有不利影响.
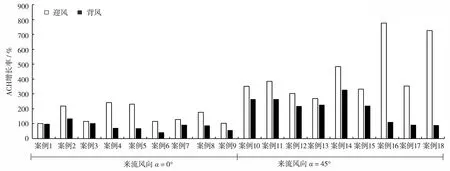
图6 迎风侧和背风侧ACH增长率Fig.6 Increase percentage of ACH in windward side and leeward side of each case
根据图6的结果,分别在来流风向为0°和45°的情况下,进一步分析上游扰流建筑和立面构件对建筑室内ACH的影响.
来流风向为0°时:① 比较案例1至案例3,对于单栋建筑,垂直立面构件在建筑的迎风侧和背风侧均明显地提高了建筑的室内自然通风换气效率,然而水平立面构件仅有轻微的提升;② 比较案例4至案例6,上游为高度比是1的扰流建筑时,两种外立面构件均对目标建筑的室内自然通风性能均有消极影响,水平立面构件使室内ACH值显著下降;③ 比较案例7至案例9,上游为高度比值是2的扰流建筑时,垂直立面构件在迎风侧提升了的目标研究建筑室内ACH值,然而对水平外立面构件在迎风侧和背风侧均对室内通风换气效率有不利影响.
来流风向为45°时:①比较案例10至案例12,对于单栋建筑,垂直立面构件在建筑的迎风侧提高了建筑的室内自然通风换气效率,然而在背风面,水平和垂直立面构件均对室内通风换气效率有不利影响;②比较案例13至案例15,上游为高度比是1的扰流建筑时,垂直外立面构件在迎风侧和背风侧均对目标建筑的室内自然通风性能有明显提升,然而水平立面构件无显著影响;③ 比较案例16至案例18,上游为高度比值是2的扰流建筑时,水平和垂直外立面构件在迎风侧和背风侧均对室内通风换气效率有不利影响,垂直立面构件在迎风侧显著降低了的目标研究建筑室内ACH值.此结果进一步表明,立面构件对建筑室内自然通风效率的影响,很大程度上受到来流风向和上游扰流建筑的干扰.
3 结 论
运用CFD模拟,根据控制变量法,分别讨论了来流风向角度、上游扰流建筑高度比以及外立面遮阳构件类型3个主要影响因素,对目标建筑周围流场和室内自然通风效果的作用,认为:
1)当来流风向为倾斜角度时,目标研究建筑通常具有更好的室内自然通风效果,例如,在45°情况下,由于来流风在建筑角部产生的流动分离形成了加速流,使建筑表面形成了气压差,成为了建筑室内外空气交换的驱动力;
2)垂直和水平外立面构件对通风性能的影响很大程度上取决于环境因素,包括近壁面的大气来流风向、目标研究建筑的方位和朝向,以及上游扰流建筑的高度比. 这些因素的综合作用改变了目标建筑的周围流场特性,使立面构件可能成为导风构件,提高室内自然通风效率,也有可能阻碍室内外空气交换;
3)尽管上游建筑物同时也对目标建筑施加了风影作用,上游扰流建筑在下游目标建筑的迎风侧和背风侧产生了复杂的流动状态,增强了目标建筑室内和周围流场区域的通风效率.

