印度库塔卡详解及其与大衍总数术比较新探
吕 鹏 纪志刚
(上海交通大学科学史与科学文化研究院,上海 200240)
数学史家对库塔卡算法的兴趣还在于其与中算不定问题解法的比较上。19世纪传教士伟烈亚力(A. Wylie)在《北华捷报》上撰文将秦九韶的“大衍术”(2)西方学者似乎并不特别区分大衍求一术和大衍总数术,而习惯统称为大衍术(Ta-yen Rule)。介绍给西方,他可能还是第一个将印度库塔卡和中算大衍术联系在一起的人。(3)伟烈亚力写道:“(大衍术)所表现的式子,或是与之类似的东西,在印度人那里被称作为‘库塔卡’(Cuttaca)。这个词可以被译为‘pulverizer’,意为无限的乘法,并且和‘大衍’的意思相差不远。此过程连同结果在印度数学中得到发现,在欧洲不仅吸引了广泛的关注,还在科学史研究中引起了一些奇特的猜测”(《北华捷报》1852年10月23号)。[6]沈康身仔细考察了库塔卡与大衍求一术的关系,指出两者在数学意义、问题情景和辗转相除方法上的相似性,并用了“平行性”一词来描述这种相似性。[7]李倍始(U. Libbrecht)在这个问题上也做过专门的研究,指出库塔卡本质是一种迭代解法,不同于大衍术使用的连分数解法,所以两者毫无联系([8],365~366页)。他的比较只依赖现代数学分析,与库塔卡或大衍术原貌都相距甚远。并且,无论是沈康身还是李倍始都没有提及用库塔卡解含三个及以上模数的同余式组的情形,而这样的同余式组正是大衍总数术的主要处理对象。因此,他们的比较工作是不充分的。本论文将就这点展现两种方法的实际计算过程,以求说明清楚库塔卡和大衍求一术,以及和大衍总数术之间确切的异同之处。
1 库塔卡算法详解
库塔卡问题的代数表达式为:
N≡R1(moda)≡R2(modb),(*1),
它可化为二元一次不定方程形式
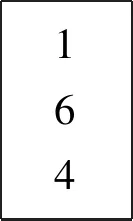
N=ax+R1=by+R2, (0≤R1 若R1-R2=c,则上式可变形为 库塔卡是古代印度数学家们的重点研究对象。这是因为它与天文计算密切相关。比如,已知在一纪(yuga,意为“会合”)周期的D日间某行星在天球上的周转圈数为R,从纪元起经过天数y时行星周转整圈数为x,并且周转不足一圈之余数为行星的黄经λ,那么根据比例关系就能得到不定关系式: 式子中的纪元常数R和D通常都是非常巨大的数,因而这里需要使用库塔卡算法来把x和y计算出来,其中y是一个以日数为单位的量,是为“上元积日”([9],185~186页)。类似的方法可以推广到求两个或更多行星的会合周期,如《婆罗摩修正体系》(以下简称《体系》)第18章6偈所说:“两个[行星]的会合周期即为两个除数的积;会合点的推移就是这两者的原余数。因此,用库塔卡算法就可以计算出三个或更多行星的会合周期”([1],326页;[10],442页),其具体做法将在后面说明。 首先看《阿耶波多历算书》是怎样来解“伴有余数的库塔卡拉”问题的。其第2章32~33两偈经文如下: 若仅加入最少量的解释性语句(方括号内),我们将上述经文直译为: (33:)下面的乘上上面的,并加入最后的。当除以有较小余数的除数时,余数乘上有较大余数的除数,再加上较大的余数,就得到被两个除数[除后有那些]余数[的数]。 从这段的经文中我们很难总结出一个完整的算法。也许阿耶波多的目的仅是希望弟子们通过吟诵这条经文来记下算法中的一些关键点。因此,为确切地理解其含义,我们求助于婆什迦罗一世的《注释》([11],132~133页)。除去纯梵语语法方面的解释之外,我们将他对经文的注释翻译如下: (32:)所谓“需用有较小余数的除数去除有较大余数的除数”,就是说对于某个除数来说,它产生出较大的余数,因此它便被称作为“有较大余数的除数”。并且这个有较大余数的除数需要被[一个数]来除。被什么[除]?被“有较小余数的除数”[来除]。所谓“[取]余数辗转相除”,就是说所得到的商没有用处,用余数来进行运算。用余数再互除便是“[取]余数辗转相除”的意思。所谓“乘上聪明数”,就是乘上靠自己的智慧[得到的数]的意思。那么,如何做才叫是乘上靠自己的智慧[得到的数]呢?这里的这个量乘上这个数,再加上或减去余数间的差后,可以得到[一个数]能整除这个量。所谓“加入余数间的差”,就是说偶数时加,奇数时减。这是根据相传不断[的传统]解释的。如此辗转相除,将商像足迹一样排列,聪明数放下面,然后最后得到的商放在聪明数的下面。 (33:)所谓“下面的乘上上面的”,[就是说]上面的量要用放在下面的量去乘。“并加入最后的”,是说加上最后的量,即最后得到的商。反反复复执行这样的运算,直到运算全部结束。所谓“当除以有较小余数的除数时,余数”,[就是说]用那个有较小余数的除数除时[所得到的]余数,即取那个有较小余数的除数和之前运算所计算出来的量相除后得到的余数。所谓“乘上有较大余数的除数”,[就是说]用有较大余数的除数乘。所谓“两除数的余数”,[就是]从两个除数得到的余数,余数就是[那些所给的]数字。所谓“加上较大的余数”,就是说[之前的结果]要加上较大的余数。这里的[两句]的意思是:用有较小余数的除数除时所得到的余数乘上有较大余数的除数,再加上较大的余数,其结果就是被两除数除的那个量。以上便解释了伴有余数的库塔卡。 紧接着文字注释,婆什迦罗又辅以多道例题来进一步演示库塔卡的解法。如其第2题为: [一个量如果除以]十二得到的余数是五,另外还知道这个量被三十一除之后[得到]的余数是七。这个量是多少? 这是要求同余式组N≡ 5 (mod 12) ≡ 7 (mod 31)中N的值。这里,阿耶波多经文中的“两个除数”便是指12和31,余数则分别为5和17。因此,12又被称为“有较小余数的除数”,31则为“有较大余数的除数”,“余数间的差”是7-5=2。基于经文和注释,库塔卡求解过程具体演示如下。 (i)“需用有较小余数的除数去除有较大余数的除数” 即是取31作为被除数,12为除数,做除法: 31 ÷ 12=2……7。 由于说第一次“所得到的商没有用处”,我们舍去2,取余数7进入下一步。 (ii)“[取]余数辗转相除” 即取前一步的除数12作为被除数,余数7为除数,再做除法。然后不断重复这一过程: 12 ÷ 7=1……5,7 ÷ 5=1……2。 由于此时数字已足够简单,停止除法。这步总共得到2个商,并且最后剩下的余数为2。 (iii)“乘上聪明数后加入余数间的差” 即通过试商找出一数m,使得它与最后的余数2的乘积加上原来余数间的差2后可以被最后除法的除数5整除: (2 ×m+2) ÷ 5=整数。 略加观察可以发现m=4。由于m=4是被试商发现的,因此它被称为“聪明数”。最后的商为 (2 × 4+2) ÷ 5=2。 (iv)“将商像足迹一样排列,聪明数放下面,然后最后得到的商放在聪明数的下面” 即将除第一次以外的商从上到下排列,之后放入聪明数和最后的商,它们好似一串足迹: 1142 对于这串数字列,婆什迦罗二世及一些注释者也称之为“商的叶蔓”(phala-vallī)。 (v)“下面的乘上上面的,并加入最后的” 经文中这句话最为费解,而婆什迦罗一世的注释也不十分明了。为此我们参考同时代婆罗摩笈多的规则([10],441~442页),发现所谓“下面的”是指数字列中的倒数第二项4,“上面的”是其上面的倒数第三项1,“最后的”就是指最后一项2。因此,这步的运算就是: 4 × 1+2=6。 之后,还需要将结果替换掉原来数字列的倒数第三项,并消去最后一项,得到: 164 (vi)“反反复复执行这样的运算,直到运算全部结束” 重复(v)的步骤,执行运算: 6× 1+4=10。 此后,数字列变为: 106 由于数字列只剩下两项,(v)的运算停止。 (vii)“用有较小的余数的除数除时所得到的余数乘上有较大余数的除数,再加上较大的余数” 取上一步的最后结果10,除以原题中“有较小余数的除数”12,得商0、余数10。余数再乘上“有较大余数的除数”31,再加上那个较大的余数7,结果为317。它便是所求的数N。即: 10 ÷ 12=0……10,N=10 × 31+7=317。 以上是“伴有余数的库塔卡”的解法,所针对的问题是含有两个模数的同余式组(*1)。对于“不伴有余数的库塔卡”或“固定库塔卡”,上面的解法同样适用,只要将不定方程(*2)中x的“乘数”a看作是“有较大余数的除数”,“除数”b为“有较小余数的除数”(其余数为0),“付数”c则是“余数间的差”。 此外,对于上面的算法还有两点需要说明。一点是,针对阿耶波多第(iii)步求聪明数时要求“加入”余数间的差,对此婆什迦罗一世的注释却是“加上或者减去”,并且说“偶数时加,奇数时减”。这里的偶数或是奇数指的其实是互除环节结束后第(iv)步数字列中的数字的个数。婆罗摩笈多的库塔卡规则对此表示得更加明确,整个互除环节时若所得的商数为奇数个时,付数的性质(符号)不变;偶数个时则相反([1],332~333页)。 另一点是,关于第(vii)步“用有较小的余数的除数除时所得到的余数……”计算的意义。根据下节的算法演示可以知道,最后数字列的最上面的那个数其实是同余式的不定方程形式中的x的解。将它除以“有较小余数的除数”后所得的余数就是方程的最小解。与此相关,有些印度数学家,如普利突大卡、婆什迦罗二世等在解不定方程形式(*2)的库塔卡问题时,通常还会保留第一次除法的商。这样迭代计算后最上面的那个数就变成了不定方程中y的解。 由于库塔卡问题可以有同余式组表示(*1)和不定方程表示(*2),下面我们就用后者 来演示库塔卡算法的一般运算程序,其目的是求“乘数”x。首先做除法a÷b,得到第一次的商q1余数r1,然后取之前的除数和余数再做除法b÷r1,得到第二次的商q2余数r2。这样反复取前一次的除数与余数互除,得到一连串的商和余数: r1÷r2=q3……r3, r2÷r3=q4……r4, … rn-1÷rn=qn+1……rn+1(使得rn+1足够小)。 除第一次得到的商数q1以外,将商排列如下: q2q3q4︙qn+1 将m和l也放在刚才的商的数字列下面,就有: q2q3q4︙qn+1ml 这之后,将其中倒数第二项乘以倒数第三项,积加上倒数第一项,所得的和取代原来倒数第三项,并消去最后一项: q2︙qi-2qi-1qi → q2︙q=i=-=2=qi-2qi-1+qiqi-1q=i= → q2︙qi-2qi-1+qiqi-1 对新数字列重复刚才的运算,直到数字列中只剩下两个数字。此时最上面的数字就是原不定方程中x的一个解α。若a=bt+a0(t=0,1,…),则得到最小解α0;将之代入原不定方程,可以得到y的最小解β0。 下面是对库塔卡算法的一般证明。(6)此处的证明综合了矢野道雄(1980)和Keller(2006)的工作。首先通过互除环节得到的商(q1,q2,…,q2p,q2p+1)和余数(r1,r2,…,r2p,r2p+1),可以获得如下一系列的不定方程: ⋮ 接下来,根据得到的商(q2,…,q2p,q2p+1)的个数的奇偶,解最后得到的关于xp或yp+1的不定方程。由于系数已化简,容易通过观察发现(yp,xp)或(xp,yp+1)的一组解,其中yp或xp的值称为聪明数m,对应的商数xp或yp+1是最后的商l。将它们连同商(q2,…,q2p,q2p+1)排成一列后,进入迭代运算环节,其本质是将最后的不定方程的一组解代入前一步的不定方程里。如此反复地代入计算,所得的最终结果就是原不定方程中x的一个解。以数字列中的商为偶数个时为例,我们用图示来说明这个迭代过程: q2q3︙q2pq2p+1m=xpl=yp+1 → q2q3︙q2pq2p+1xp+yp+1=ypxp → q2q3︙q2pyp+xp=xp-1yp →… q2q3q4y2+x2=x1y2 → q2q3x1+y2=y1x1 → q2y1+x1=xy1 上面1.1节的库塔卡例题涉及到的是已知某数分别除以两个除数得到相应余数时如何来求这个数。当除数(即同余式组中的模数)有三个或三个以上时,仍可用库塔卡来解,正如前面所引婆罗摩笈多的话:“可以计算出三个或更多行星的会合周期”。至于具体如何操作,我们援引普利突大卡在注释《体系》这部分时所提供的一道例题([1],326页): 什么数除以六时有余数五,除以五时有余数四,[除以]四时有余数三,[除以]三时有[余数]二? 问题可表示成含有4个模数的一次同余式组:N≡5(mod 6)≡4(mod 5)≡3(mod 4)≡2(mod 3),求N。特别地,这里模数并非是两两互素。普利突大卡所提供的解法是,先取头两个除数(同余式的模数)6和5及它们对应的余数来施行库塔卡,即解同余式组N1≡5(mod 6)≡4(mod 5)。首先进行算法第(i)(ii)步的辗转相除: 6÷5=1……1,5÷1=5……0; 由于这里余数为0,所以(iii)中要找的聪明数m可以取任意值,这是因为: (0×m-1)÷1=-1。 不妨取m=1,得到(iv)的“商的蔓”,即数字列:5、1、-1。进行一次(v)的计算后,数字列剩下两项:4、1。因此,所要求的 N1=6×4+5=24+5=29。 需要注意的是,在这里的解题过程中虽然遇到了涉及0和负数的计算,但这对印度数学家们来说不构成丝毫的问题。因为婆罗摩笈多在《体系》第18章30~35偈中已给出了全套关于0和负数的计算规则([10],442~443页)。 再回到例题,接下来普利突大卡按照婆罗摩笈多的指示,把刚才的头两个除数的乘积视为一新的除数,N1为相应的余数,连同原同余式组中的第三个除数(模数)和其余数再次施行库塔卡,即解N2≡29(mod 30)≡3(mod 4)。(7)容易证明:若N≡R1(moda)≡R2(modb),则N′≡N(moda·b)≡R1(moda)≡R2(modb)。过程如下: 30÷4=7……2,4÷2=2……0; (0×m-26)÷2=-13→m=7。(8)这里m取7的理由是使下一步(也是最后一步)的计算结果为一个非负数。 得到“商的蔓”:7、2、-13。进行一次(v)的计算,得到:1、2。因此 N2=30×1+29=59。 然后可以重复刚才的办法,解N3≡59(mod 60)≡2(mod 3)。(9)有意思的是,这里普利突大卡在实际演算中并没有单纯取30和4的乘积120作为新的模数,而是它们的最小公倍数60。其理由将在下节说明。只不过在此之前我们发现N2的值59已能满足最后“[除以]三时有[余数]二”的条件,因此计算到处结束,所求N的最小解就是59。 综上所述,若要用库塔卡算法解同余式组 N≡R1(moda1)≡R2(moda2)≡R3(moda3)≡…≡Rn(modan), 可以先解出N1≡R1(moda1)≡R2(moda2),然后再解N2≡N1(moda1a2)≡R3(moda3)。重复此过程,最后求解同余式Ni-1≡Ni-2(moda1a2…an-1)≡Rn(modan),其解Ni-1就是要求的N。 针对含三个及以上模数的同余式组的方法,即婆罗摩笈多所教导的取“两个除数的积”的方法,9世纪《体系》的注释者普利突大卡还做了这样的说明: 此处的积应理解为产生较大余数的除数与产生较小余数的除数除以[两者]共同量(即最大公约数)之后所得商的积([1],327页)。(10)容易证明:若N≡R1(moda)≡R2(modb),则N′≡N(moda·b)≡R1(moda)≡R2(modb),L为a、b的最小公倍数。当a、b互素时,L=ab。 开始库塔卡之前,若可能的话须将被除数、除数和付数约去一共同之数([12],166页); 同书第35偈: 没有付数或付数能被除数整除时,乘数[的解]为零,商当认为是付数除以除数所得结果([12],202页)。 在此之前的印度数学家可能也意识到了这些关系,比如说我们发现婆什迦罗一世尽管没有明确说明这条规则,但他在实际计算过程中会先同时约去b、c项的最大公因数,然后在解得x后再乘以这个公因数([5],162页)。不管怎么说,婆什迦罗二世将库塔卡算法朝机械化和程序化的方向做了很大的推进,依照他的规则我们已经编写出了一套程序在计算机上实现了库塔卡算法。 也许是出于历法中计算历元的需要,中国也从较早的年代开始意识到不定分析问题。公元4世纪前后的《孙子算经》有“物不知数”题,便是要求解含有三个模数的同余式组N≡R1(moda1)≡R2(moda2)≡R2(moda3)。分析其中所给的算法术文,可以总结出中算的解法是先找出辅助系数K1,K2,K3,使如下同余式成立: K1a2a3≡1(moda1),K2a1a3≡1(moda2),K3a1a2≡1(moda3)。 接着,所求的N便可由下式求得: N≡R1K1a2a3+R2K1a1a3+R3K3a1a2(moda1a2a3)。 这种求解的程序后世称呼为“孙子定理”或“中国剩余定理”。其中余数Ri和模数ai都是已知量,且ai两两互素。在数字相对简单的情况下,辅助系数Ki可以通过观察试算得出;当数字较复杂时,或是模数并非两两互素时,解的获得就变得相当困难。 中算文献中真正完整的同余式组解法是秦九韶在其《数书九章》(1247)中所给出的“大衍总数术”。该术又可分为两个大的部分,其一是约化模数的过程,即“化问数(原模数)为定数(约化后互素的模数)”。其二是根据“定数”计算“乘率”,即上述辅助系数Ki,使得 Kigi≡1(modai),(*3), 其中gi被称为“奇数”,是除ai以外的模数的乘积除以ai后的余数。通过这两步求得乘率Ki后,就可以利用“孙子定理”求出最后的结果N。 大衍总数术中求乘率的步骤即为“大衍求一术”,其术文摘录如下: 置奇右上,定居右下。立天元一于左上。先以右上除右下,所得商数与左上一相生,入左下。然后乃以右行上下,以少除多,递互除之。所得商数,随即递互累乘,归左行上下。须使右上末后奇一而止。乃验左上所得,以为乘率。[13] 下面就以问题K×7≡1(mod25)为例,演示大衍求一术的解题过程。 (I)“置奇右上,定居右下。立天元一于左上” 奇数是7,定数为25,它们连同数字1按以下样子排布: 1奇数7定数25 (II)“以右上除右下,所得商数与左上一相生,入左下” 即以定数25除以奇数7,所得余数4代替原来的被除数25放于右下,商3乘以除数的左边这列中上方的数1后放入被除数左边空位: 1725 25÷7=3…4→3×1=3 1734 (III)“然后乃以右行上下,以少除多,递互除之。所得商数,随即递互累乘,归左行上下。须使右上末后奇一而止” 将右列数字以小除大辗转相除,余数替换被除数,商乘上除数左列数字后加入被除数左列数字。重复此过程直到右上位的数变为1为止: 1734 7÷4=1…3→1×3+1=4 4334 4÷3=1…1→1×4+3=7 4371 3÷1=2…1→2×7+4=18 18171 此时左上数字18便是乘率。经检验符合要求:18×7=126,126≡1(mod25)。 首先,可以将上面大衍求一术所要解决问题的基本形式(*3)做一个变换,得到 数字列-1迭代计算数字列-2迭代计算(q1)q2q3︙qn-1qn10K0=l=0,K1=m=1,K2=qnK1+K0=qn,K3=qn-1K2+K1=qn-1qn+1,…Kn+1=q1·Kn+Kn-1。↑计算方向01q1q2q3︙qn-1qn计算方向↓J0=0,J1=1,J2=q1J1+J0=q1,J3=q2J2+J1=q1q2+1,…jn+1=qn·Jn+Jn-1。 沈康身已用数学归纳法证明了上面用固定库塔卡和大衍求一术分别计算出的迭代结果两者等价:Kn+1=Jn+1。[14] 库塔卡(固定库塔卡)和大衍求一术不光有着等价的问题形式(二元一次不定方程),通过上面的分析还能清楚看到两者在解法上的相似性。具体来说,它表现为:(1)两者的基本思路都是通过辗转相除的办法将原不定方程系数化至最简,并利用此过程中得到的商数进行迭代计算,而迭代的最后结果就是要求的解;(2)伴随着相同的基本思路,两种算法操作起来都有高度的机械化和程序化的特点,并且都规定了独特的数字阵型(商的蔓和方阵)以保证运算的正确和效率。 然而另一方面,库塔卡和大衍求一术解法之间的差异也是很明显的,主要表现在:(1)两种解法的运算顺序不同,库塔卡是先完成互除然后再进行迭代,即将所有的商数列出后再从后往前计算,一气呵成。大衍求一术则是除法和迭代同时进行,随除随算,节省了数据储存空间[15]。(2)库塔卡没有像大衍求一术那样规定互除次数必须是偶数次。(3)在迭代计算的环节中大衍求一术实际规定了用于计算的头两项必须为0和1,而在固定库塔卡,或者说更一般的库塔卡算法中则没有这个限制条件,只要是满足最后互除所得到的不定方程的解都可以。因而相比较而言,库塔卡的计算过程更加自由和随意一些。 上节就库塔卡(固定库塔卡)与大衍求一术之间做了一番基于问题形式和解法层面上的比较,比较的结果是两者确实在算法结构上有着诸多相似或是说等价的地方。然而,如果我们换一个视角,即从解不定分析问题这个目的出发就能意识到,库塔卡的真正比较对象并不能仅局限于大衍求一术,而应该是它的“母体”大衍总数术。前面的解说中库塔卡虽然大都以二元一次不定方程的形式呈现,但它其实和大衍总数术一样,都是设计出用来解含有多个模数的一次同余式组,即已知N≡R1(moda1)≡R2(moda2)≡R3(moda3)≡…≡Rn(modan),求N的问题。至少从婆什迦罗一世开始印度人就已采取反复使用库塔卡的方式来解决;中算虽有孙子的特殊情况(模两两互素)时的解法,但系统化的算法还需等到13世纪秦九韶的大衍总数术。换句话说,库塔卡虽然在算法上和大衍求一术有相似性,但它的解题能力其实等同于大衍总数术。为了说明这一点,下面举例看看如何用库塔卡来解秦九韶的大衍问题。 《数书九章》“大衍类”中的第八问为“积尺寻源”题([13],461页),它可化为下面两个同余式组: N≡60(mod 130)≡30(mod 120)≡20(mod 110)≡30(mod 100) ≡30(mod 60)≡30(mod 50)≡5(mod 25)≡10(mod 20); M≡-60(mod 130)≡-10(mod 120)≡-30(mod 110)≡10(mod 100) ≡-10(mod 60)≡10(mod 50)≡10(mod 25)≡10(mod 20)。 以第一个关于N的同余式组为例,用大衍总数术解这道题时首先要对所有8个模数进行约化,经过“两两连环求等”约化后的同余式组为: N≡60(mod 13)≡30(mod 8)≡20(mod 11)≡30(mod 3)≡5(mod 25)。 然后从它可以得到5个形如(*3)的单个同余式: K1×9≡1(mod13),K2×5≡1(mod8),K3×1≡1(mod11),K5×1≡1(mod3),K7×7≡1(mod25)。 用大衍求一术分别求出解乘率Ki,再通过“孙子定理”得到最小整数解1230。 作为比较,我们试用库塔卡来解此题。遵照婆什迦罗一世的做法,先取头两个同余关系,解同余式组N′≡60(mod130)≡30(mod120),即有不定方程 此处系数a、b、c有共同的因数10,根据前述婆什迦罗二世《算法本源》26的规则,可将10约去,得到 用库塔卡方法,先进行互除: 13÷12=1……1,12÷1=12……0。 聪明数m和最后的商l为: (0×m-3)÷1=l→m=7,l=-3。 商的蔓就为12,1,-3。经一步迭代计算后得x′=9,因此y′=10,N′=1230。接着取头两个除数(模数)130和120的最小公倍数1560作为新的除数(模数),N′作为对应的余数,连同原式中的第三个同余式,解新同余式组N″≡1230(mod 1560)≡20(mod 110): 此处121可被11整除,根据婆什迦罗二世《算法本源》35的规则,得x″=0,y″=11,N″=1230。类似地,可以发现1230≡30(mod100)≡30(mod60)≡30(mod 50)≡5(mod25)≡10(mod20),因此最后的解N=1230。对于原题中的另一个关于M的同余式组,运用与上面类似的方法也可以方便地求得M=3710,在此就不再展开。 通过具体演算可以发现,用库塔卡来解秦九韶题更为简单便捷,过程中实际只解了两个不定方程。这主要是因为在使用库塔卡时可以直接对除数和余数进行约化,因而无需考虑模数的互素性。此外,在阿耶波多-婆什迦罗一世的库塔卡算法基础上,婆罗摩笈多和婆什迦罗二世等人所补充的那些辅助规则对提高计算效率也非常有帮助。并且我们还看到,印度数学家能熟练使用0和负数进行计算也是库塔卡算法优于大衍术的一个重要因素。 正如沈康身先生指出“关于不定分析问题中印互相影响,甚至师承关系问题,素为海内外学者所关注”。比如,印度数学史家森(S.N.Sen)和巴戈(A.K.Bag)就认为中国大衍求一术来自印度,库塔卡是一恰当的鉴定根据([8],361~362页;[14],267页);李倍始却持不同意见:“我们不能接受中国大衍求一术与印度库塔卡有任何历史渊源关系”。沈康身认为对于这个问题“不宜急于作出结论……(需要)对不定分析的来龙去脉各自在理论上和实际计算方法上的相同处和不同处进行客观分析和比较”([14],267~268页)。因此,沈康身用“平行性”来描述中印两民族的同余式研究。 就库塔卡和大衍求一术而言,本文同意沈康身等学者对相似性的判断,但具体细节有所不同。经过对原典文献的解读和算法分析比对,我们指出库塔卡的一种特殊类型,即固定库塔卡的确与大衍求一术存在着算法结构上的相似性和数学原理上的等价性。然而,两者的“母体”,即库塔卡和大衍总数术之间却不存在着那样的相似性,由此两者间也很难存在渊源关系。虽然这个结论和李倍始的一致,但他的分析几乎完全是基于现代数学认识之上([8],363~366页),缺乏对算法原貌的重构和历史演变的分析。 本文认为,应该基于库塔卡与大衍总数术展开“中印同余问题”的比较研究。 首先,库塔卡是固定库塔卡更加一般的形式,算法本质上相同;大衍求一术却是大衍总数术中的一个环节,与它之前的模数约化,以及之后用“孙子定理”求解的环节都紧密相连。换句话说,库塔卡可以看作是能对模数进行约化处理的大衍求一术,其中接连使用联立同余式的方法则可看成是“孙子定理”的一种表达。因而,库塔卡和大衍总数术在总的结构上没有可比较之处,也不存在印度学者所主张的大衍求一术单独借鉴库塔卡的可能性。 再者,印度库塔卡于5世纪首先出现在《阿耶波多历算书》中以后,算法层面上基本没有太大的变化,并且它一开始就有处理任意一次同余问题的能力。中国先是在3~4世纪时有处理模数两两互素的同余问题的方法,但之后很长时间没有发展,直到13世纪秦九韶补充上了约化和求乘率(大衍求一术)的规则形成大衍总数术后,才可以处理任意一般问题。因而,库塔卡和大衍总数术各自的发展历史也是大不相同。 最后,也是在上述两点的基础上我们认为,即便库塔卡(固定库塔卡)和大衍求一术有着一些相似性或等价性,但它不能说明中印在此问题上有过交流。这里的相似性很可能是不同文明在数学发展过程中的一种巧合,因为两者的母体——库塔卡和大衍总数术——之间无论是从结构上还是历史上来说都有着更加明显的差异。并且,这种差异还体现在计算便捷性上,我们举例说明过库塔卡要优于大衍总数术,因而就这点来讲也很难想象出两者间有过传播或借鉴。 当然,库塔卡与大衍总数术的相互独立性,并不能否认中印之间在其他数学知识和文化上存在相互交流与影响的可能性。 致 谢审稿过程中两位专家和邹大海研究员都为本论文提出了中肯切实又富有建设性的意见,谨此深表感谢!

1.1 阿耶波多-婆什迦罗一世的解法





1.2 库塔卡算法的一般步骤及其证明






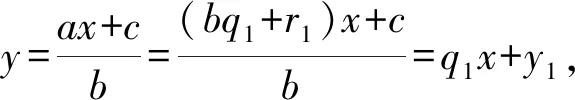
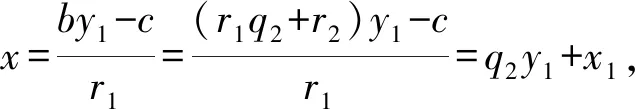

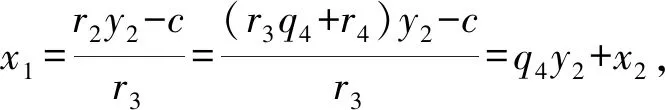
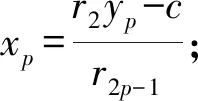


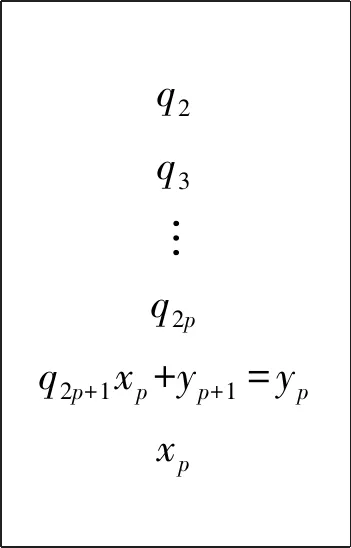
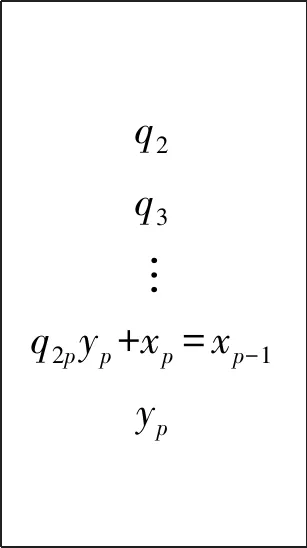
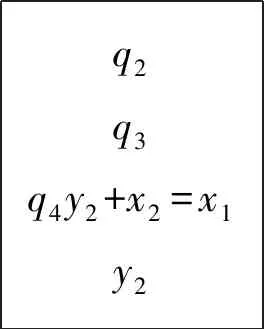
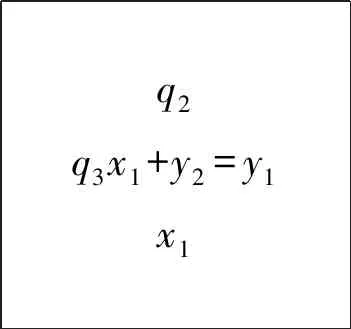
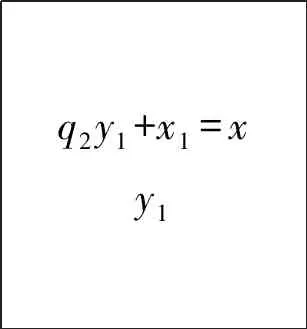

1.3 含三个及以上模数的同余式组的解法
1.4 库塔卡算法在印度的发展与完善


2 库塔卡与大衍总数术异同比较




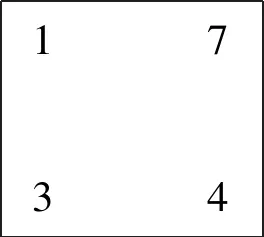
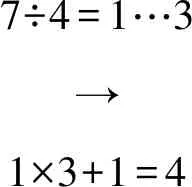



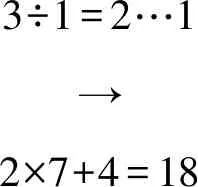
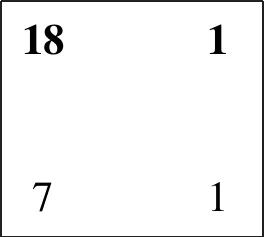
2.1 库塔卡与大衍求一术解法异同



2.2 库塔卡解大衍总数术题
2.3 库塔卡与大衍总数术之比较

