轴流风机内三维流场及进出口气动噪声的数值模拟

王妮妮，王琳，安春国，汪坤，李志远，李俊，高明*

（1.山东电力工程咨询院有限公司，济南 250013；2.山东大学能源与动力工程学院，济南 250061；3.安徽微威减震降噪技术研究院，安徽 桐城 231460）

引言

动叶可调轴流风机通过改变动叶安装角可实现工况调节，适应性强且高效节能，已逐步成为大型火电厂送风机和引风机的主流选择[1]。但其进出口的气动噪声严重影响了风机正常运行，恶化了人们的工作和生活环境，因此，研究动叶可调轴流风机的流场特性和噪声规律具有重要的现实意义。

目前，主要通过数值模拟和实验等方法进行动叶可调轴流风机的流场和声场特性规律研究。李春曦[2]在LES大涡模拟的基础上，结合以Lightlill声类比为基础的FW-H模型，模拟得到了安装角异常时风机声源强度分布和不同区域的气动噪声时频特性，发现安装角异常叶片增强了动叶区宽频噪声特性，分散了其他区域在低频段的离散峰值。Liu[3]等研究轴流风机前置导流叶片的出口角对整体气动性能的影响，发现在额定工况下，随着出口角度的增加，风机的静压和效率先增加后降低，在模拟的出口角度范围内，60°为最佳性能角度。

本文通过Fluent对动叶可调轴流风机的流动和噪声进行数值模拟，引入波动方差的比率[7]总结壁面压力脉动随安装角的变化规律[8]，为改进和开发高性能且低气动噪声的动叶可调轴流风机提供理论基础。

1 数值模拟基础

1.1 数值模拟模型

1.1.1 FW-H方程

FW-H方程可以准确描述流体与运动物体相互作用而产生的声音问题[6、7]，其本质是把N-S方程整理成非齐次波动方程式：

式中：a0为声音在空气中的传播速度（m/s）；为声压（Pa）；为控制面法向速度分量（m/s）；为流

1.1.2 Standard模型输运方程

Standard模型作为稳态模拟的湍流模型，其具有稳定性、经济性和较高的精度等优点[8]。其输运方程如下：

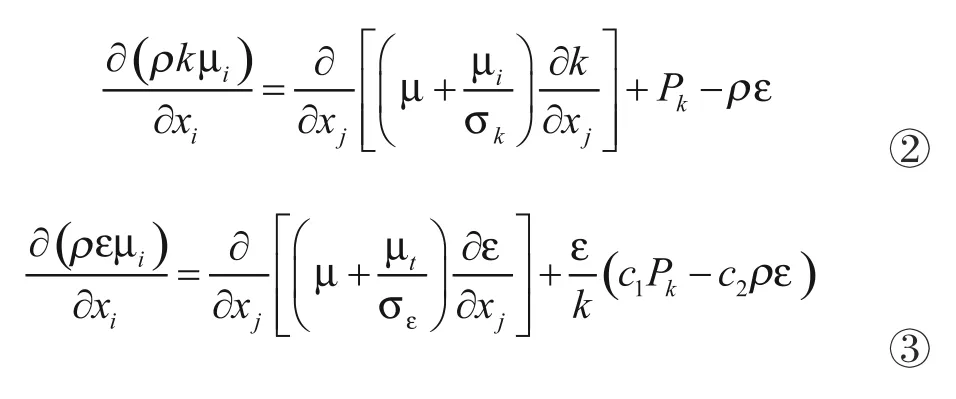
1.2 数值模型验证

表1给出五个风机额定工况点的出厂设计安装角、流量和出口全压数据。

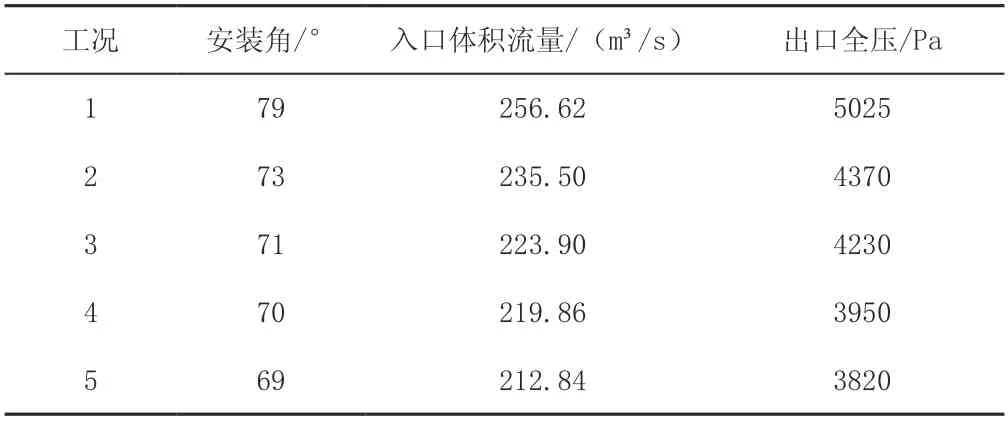
表1 额定工况点出场设计值

对比五种工况出口全压的模拟值与设计值验证模型准确性，结果见图1。

由图1可看出，出口全压的模拟值总是大于设计值，原因有：1）网格数量影响，在网格数量足够大的情况下，模拟值会逼近设计值；2）Fluent模拟时进行了部分简化假设，不能完全吻合实际情况。但模拟结果的趋势与设计值一致，而且最大相对误差约为3.7%，在允许范围内[8]，因此可以保证该模型的准确性。

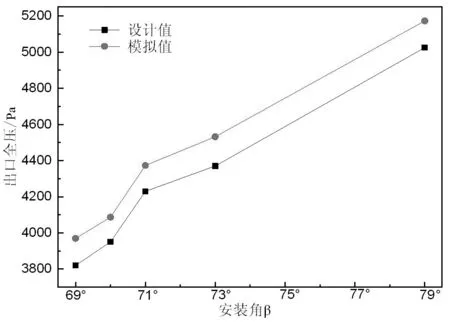
图1 全压值对比结果图

1.3 模型网格划分与验证

动叶可调轴流风机的物理模型和网络划分结果分别如图2、图3所示。网格无关性验证，如表2所示。

图2 风机计算模型图

图3 风机网格系统图

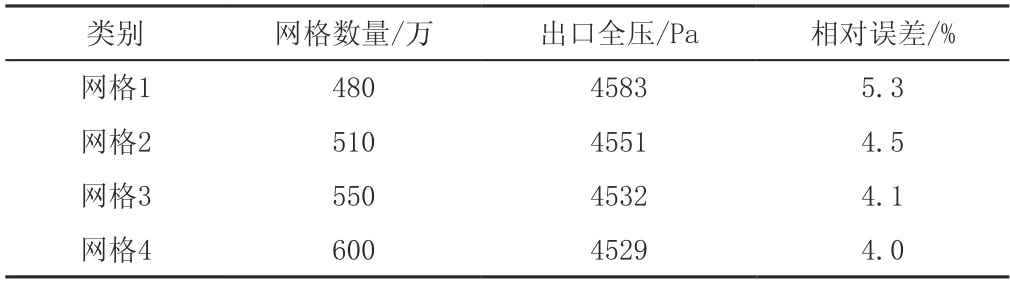
表2 网格独立性分析

从表2可看出，随着网格数量的增加，计算得到的出口全压值越来越接近设计值，但对比550万和600万网格数量，两者的模拟值差别基本可以忽略。考虑到计算时间和成本，选用网格3的网格数量级进行后续的计算，而且该网格计算的相对误差为4.1%，在合理的范围内，可以保证计算模型的准确性。

2 流场和声场模拟

2.1 流场模拟

2.1.1 稳态流场

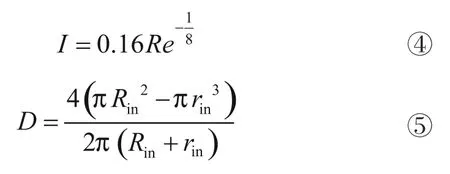
根据上述边界条件和稳态计算设置模拟了额定安装角下风机的稳态流场，通过内部流线图和叶片压力云图[11]定性验证数值模拟边界条件和参数设置正确性。

2.1.2 稳态计算设置

稳态计算时湍流模型设置为Standard模型，近壁面处理设置为标准壁面方程，由于本文不考虑温度变化对气动噪声的影响，因此控制方程不开启能量方程，仅考虑质量守恒和动量守恒方程；动叶轮区设置为多参考系模型[11]（Moving Reference Frame,MRF），可对独立的计算区域指定不同的旋转速度，但在计算过程中，MRF模型的计算区域之间网格不会发生相对运动，该模型仅适用于稳态计算，计算出的流场是充分发展的流场，采用MRF模型时，设置风机叶轮的转速为990r/min；由于本模拟的介质假定为不可压流体，采用压力基隐式求解器[12]，选择SIMPLE算法[13]来耦合压力和速度，各项气动性能的指标参数设置为二阶迎风，当各计算残差值小于给定标准1×10-5时，认为计算收敛。

2.1.3 额定工况的流场分析

根据上述边界条件和稳态计算设置模拟了额定安装角下风机的稳态流场，通过内部流线图定性验证数值模拟边界条件和参数设置的正确性，图4为风机整体流线分布。

图4 风机整体流场流线图

由图4可知，气流以直线流动的方式进入喇叭口；然后接触动叶轮，通过叶片与气流周期性作用产生升力，提高流体压头。气流在叶轮内的速度沿叶高方向逐渐升高，该区域内的气流速度最大；最后气流经过静叶片的导流作用，从紊乱趋于稳定，流动呈现较小范围的螺旋状[14]。

2.2 声场模拟

基于流场的计算结果，Fluent通过计算时域积分和面积分求解FW-H方程以获得风机进出口噪声声压级随安装角的变化规律[2]。在距离进口面和出口面中心1m的水平位置设置噪声监测点，如图5所示。通过比较不同的噪声源面对气动噪声的影响，最终选定机壳+叶轮为噪声源面，如表3所示。

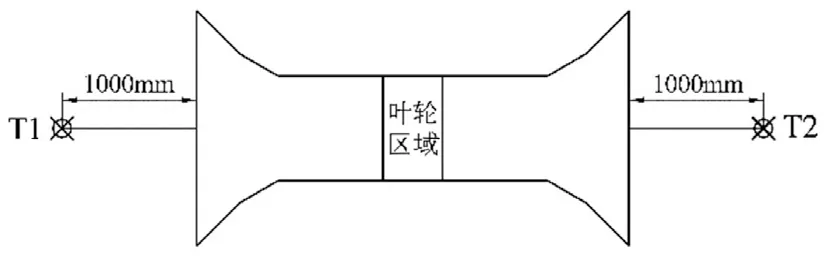
图5 进出口测点

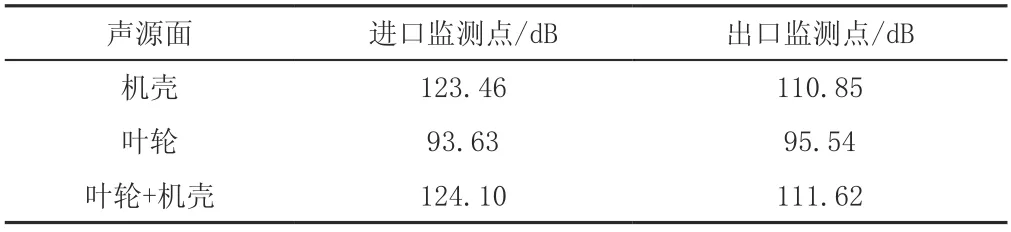
表3 不同声源面的计算结果

2.3 进口和出口噪声变化规律

随着风机叶片安装角的变化，风机进出口测点声压级变化规律如图6所示。

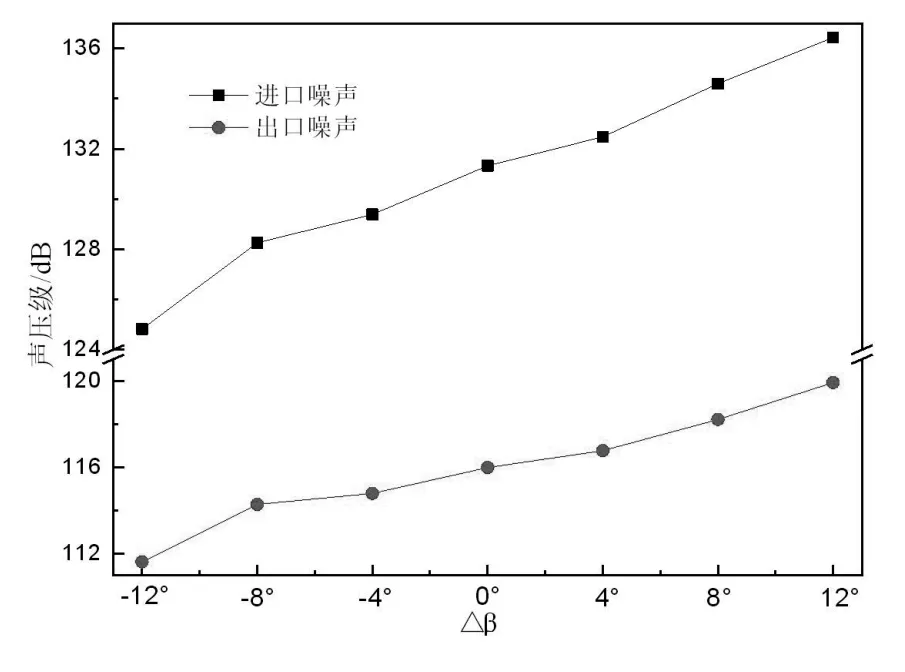
图6 进口和出口噪声声压级变化曲线图

由图6可知，对于进口噪声，△β由-12°偏转到12°，声压级共增加了11.6dB，其中，△β从-12°偏转到-8°时，声压级变化幅度最大，增加了3.4dB，占总变化值的29.3%。对于出口噪声，△β从-12°偏转到12°，声压级共增加了7.3dB，其中，△β从-12°变偏转到-8°声压级变化幅度最大，增加了2.7dB，占总变化值的37%。

2.4 壁面压力脉动规律

轴流风机气动噪声的产生与壁面和流体的相互作用力有关[7]，引入波动方差的比率CD总结壁面压力脉动随安装角的变化规律。

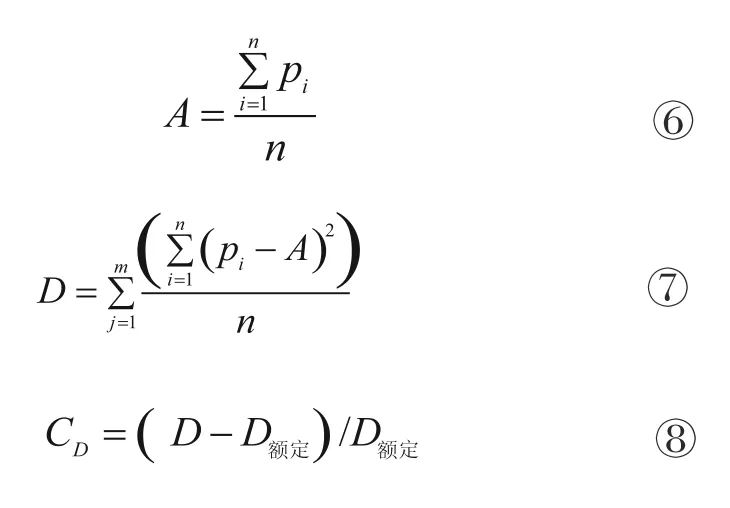
式中：m为机壳、叶轮、轮毂上的监测点数量；n为采样步数，即叶轮转动一个流道的时间。

风机壁面压力脉动率变化随安装角变化如图7所示。

由图7可知，壁面的压力脉动程度逐渐增加，安装角从△β=-12°偏转到△β=-8°时，CD值变化幅度最大，说明声压级增加幅度最大。

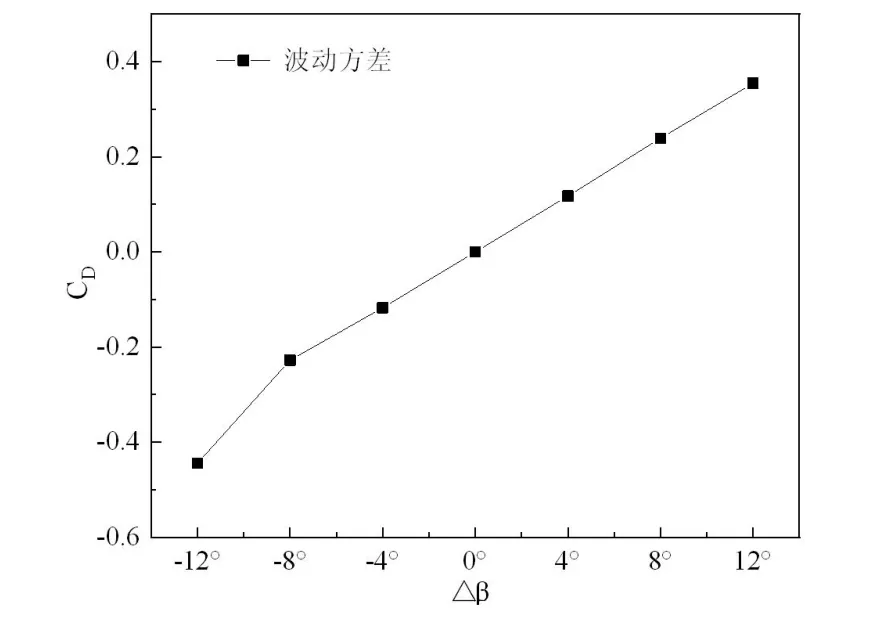
图7 风机壁面压力脉动率变化随安装角变化的曲线图

3 结论

基于Fluent数值模拟，分析了动叶可调轴流风机稳态流场的流线分布，总结了动叶可调轴流风机进出口噪声和风机壁面压力脉动率随安装角的变化规律。

（1）气流受到动叶的升力作用后，在叶轮内的流速最大且沿叶高方向逐渐增加，而后经过静叶片导流，流动趋于稳定并呈现较小范围的螺旋状。

（2）△β由-12°偏转到12°，进出口噪声声压分别增长了11.6dB和7.3dB，进出口噪声均在△β从-12°偏转到-8°时，声压级变化幅度最大，分别增加了3.4dB和2.7dB，其他工况下，安装角每正向偏转4°，进口噪声声压级增加1～2dB，出口噪声声压级增加0.5～1.5dB。

（3）壁面的压力脉动程度随安装角的增大而逐渐增加，CD值在安装角从△β-12°偏转到△β-8°时变化幅度最大，说明声压级增加幅度最大，且CD值逐渐增加与声压级变化规律相符。

研究结果表明，动叶可调轴流风机进出口噪声声压变化规律与壁面的压力脉动随安装角变化规律一致，且声压级和压力脉动均在安装角从△β-12°偏转到△β-8°时变化幅度最大，验证了实验结果的正确性。