小学生简便运算错误多的原因分析与对策

【摘要】本文针对小学生简便计算错误多的现象，分析其成因，提出给学生增加简便运算的机会，通过模型、图形、文字等形式表征运算定律，帮助学生深度学习等教学建议。

【关键词】简便运算 计算 多元表征

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2019）09A-0132-02

教师普遍有这样的感受：简便运算的新授课阶段，不管是例题还是练习，学生学得开心、轻松，正确率也高。但当简便计算各种类型混合在一起时，尤其是期末总复习时，简便计算就会成为“查漏补缺”的重灾区，各种错误让教师措手不及。

笔者认为，学生简便计算容易出错的原因有以下几点。

首先，简便计算意识淡薄。《义务教育数学课程标准》（2011年版）降低了对计算能力的要求，于是，一些教师曲解了新课标的要求，认为简算就是掌握运算定律，忽视了学生简算意识的渗透与培养，导致学生普遍认为题目中有简算要求时，要用简便方法计算，没有简算要求时，就可以不用简算方法计算。简算是快速计算的途径，教师不应该狭隘地将它划为与其他知识毫无关联的知识点。学生平时缺乏简算应用意识，根源在于教师认识不到位。

其次，教材集中编排，学生容易混淆。在编排五大运算定律、两大运算性质a-b-c=a-（b+c）与a÷b÷c=a÷（b×c）时，人教版教材采用集中编排的方式，四年级下册《运算定律》单元一共呈现了8道例题。对部分学生来说，前后相似的规律容易形成干扰，使他们混淆。同时，简算题型多、变化丰富、综合性强，有些题目还可以一题多解等，这些都给学生的学习增加了难度。

最后，教学局限于“算一算”，缺少生活经验与图像模型的支撑。在日常课堂教学中，有的教师省略了运算定律形成的探究过程，通过“算一算”得出两边相等就直接推导出运算定律。学生被动接受新知，机械记忆运算公式，头脑中的运算定律缺少生活经验与图像模型的支撑，导致理解不深刻。

针对上述现象，笔者结合教学实际，提出如下解决简便运算“错误多”的策略。

一、平时增加简算机会，强化简算意识

简便运算单元教学结束后，教师可在后续教学其他内容的例题或习题时，有意识地选择凑整数据，经常性地为学生提供简算训练机会，反复强调简算“加快计算速度，提高正确率”的优点，促使学生形成“能简便计算的，就用简便方法计算”的习惯与思维定势。

例如《多边形的面积》这一单元，涉及大量面积计算，教师编写巩固习题过程中可以对数据进行选择与调整。人教版教材五年级上册第90页第八题“用木条做成一个长方形框，长18cm，宽15cm，它的周长和面积各是多少”。在实际教學中，教师可以改数据为“长28cm，宽25cm”，在计算面积时，引导学生分别计算28×25和（4×7）×25=7×（4×25）。学生计算后，呈现两种不同计算过程，通过对比，让学生感受简算的优点。

为了克服知识之间存在相似性导致学生混淆的问题，实现让学生明确算理、深刻理解运算定律的目的，在新知教学、巩固训练等环节，教师可组织学生利用模型、图形、文字、符号等多种形式来表征运算定律，帮助学生深度学习。

二、情境教学，在操作中以“移”引“算”

为了激发学生学习兴趣，引导学生主动探究运算定律，教师在教学时可创设情境，提供一些学生喜闻乐见的学习素材，让学生在具有深度思维的交流、操作、探究中感悟规律。例如“减法运算性质”的教学。

教师通过故事情境引入：小松鼠在楼上看书，听到从楼下传来妈妈的声音：“宝贝，拿14根棉签棒下来。”过了一会儿，又听到楼下传来妈妈的声音：“宝贝，再拿16根棉签棒下来。”如果你是小松鼠，你会怎么做？

生1：先取出14根棉签棒下楼拿给妈妈;再取出16根棉签棒下楼拿给妈妈。

生2：取出30（14+16）根棉签棒下楼拿给妈妈。

师：如果楼上原来有52根棉签棒，还剩几根？用老师这里的52根棉签棒，把你刚才介绍的拿法示范给大家看。[生1移动棉签棒，得到算式52-14-16=22（根），生2移动棉签棒，得到算式52-（14+16）=22（根）]

师：大家更喜欢谁的方法？为什么？

生3：我更喜欢第二种方法，因为可以把两次需要的棉签棒合在一起，一次性拿下楼，完成任务。

师：如果用字母a、b、c表示这三个数，这个规律可以怎么表示？

生：a-b-c=a-（b+c）。

在这一过程中，学生从已有的认知经验出发，操作实物，用自己的语言表述想法;借助情境，经历操作表征、语言表征、符号表征，学生更加高效地学习。情境的设置、生活经验的支撑、多元的表征形式，兼顾了不同层次、不同认知的学生，让他们都能以自己的认知方式，多角度地感知规律，实现对规律的深度建构。

三、巧用图形，在创作中以“画”明“理”

在平时教学中，教师可以利用课余时间布置探究作业，让孩子自己创设情境，用画图的方式表达规律，厘清算理，加深理解。

乘法分配律是五大运算定律中应用最广的，也是错例最多的。教学时，教师可以这样布置相应的探究作业：

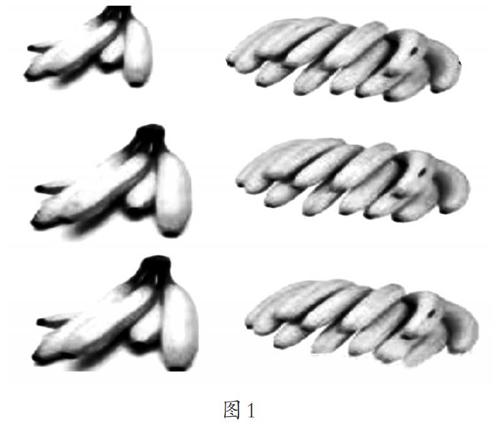
（1）香蕉图里你能发现乘法分配律吗？这里一共有几根香蕉？请用不同颜色的笔圈出（5+12）×3是怎么数的，5×3+12×3又是怎样数的？

（2）请你为（4+6）×3=4×3+6×3配一幅图。你可以自己写式子画出“分配律”，也可以自己画个图让我们来猜式子哦。（下面是学生的作品）

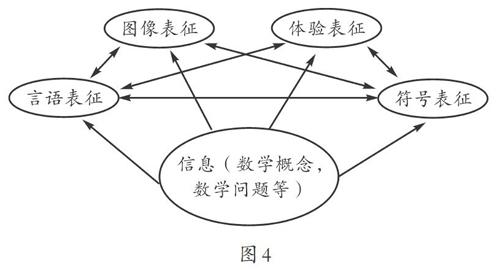
学生在完成探究作业的过程中，收集了丰富的素材，自觉地把情景、图像、书面语言、符号语言等多元表征形式实现融合与联结（如图4）。借助创作，从多个角度对规律进行解释，使学生对规律有多层次、多角度的感悟，真正实现知识内化。

四、语言表述，在综合训练中以“辨”析“法”

灵活、综合地运用相关定律，实现简便运算的策略多样化与优化，需要大量综合训练的支撑。教师可提供丰富的题组，组织学生在解题的过程中明晰方法、减少错误。

例如，（1）计算125×16，想想怎么算又对又快。

学生大胆探索，想到多种方法。教师一一呈现，同时让学生说说他们根据什么运算定律计算。

①125×16=125×（10+6）

②125×16=125×4×4

③125×16=1000×16÷8

④125×16=（100+25）×16

⑤125×16=125×8×2

⑥125×16=（125×8）×（16÷8）

（2）呈现学生竖式计算的过程，让学生思考，竖式计算与以上第几种方法用了相同的运算定律？

心智哲学相关理论认为，语言活动是心智活动的反映，认为语言的意义建构及理解依赖感知经验，是多模态感知与感知信息加工的结果。综合练习中的思维碰撞与语言辨析，有利于将相似的、模糊的感知转为清晰的、明了的结论，有利于减少混淆，提高简便运算的正确率。

简便运算是一种高级的混合运算，不仅是锻炼学生思维灵活性的重要手段，而且是培养学生数学思维和逻辑推理能力的重要途径，理应受到足够重视。

【参考文献】

[1]冯莉秋.左崇良.小学数学简便运算问题及改进策略[J]教育与教学研究.2018（10）

[2]刘春莲.黄涛.巧用多元表征，促进规律形成[J]江西教育.2019（2）

[3]戴滢.关于在小学数学课堂中展开有效运算教学的策略分析[J]数学学习与研究.2018（12）

[4]庄成珠.小学低中年级计算教学多元表征的运用[J]福建基础教育研究.2016（12）

[5]魏美花.小学数学简便计算错误成因分析[J]数学学习与研究.2015（14）

作者简介：竺君婓（1972— ），女，浙江奉化人，小学高级教师，大学本科学历，宁波市学科骨干教师。研究方向：拓展课程、计算教学。

（责编 刘小瑗）