锥束X-CT系统四椭圆法获取全几何参数的研究

张 震， 宋卫东， 张丰收

(河南科技大学 医学技术与工程学院， 河南 洛阳 471000)

锥束X-CT系统相比传统CT系统有许多优点，随其不断发展，在医学成像和工业无损检测中占据着重要地位。其成像质量受制于安装误差，安装误差如果不加以校正，会引起重建图像出现环形伪影[1]，所以对锥束X-CT系统进行几何参数标定是很有必要的。近年来各种标定方法层出不穷，其中Sun和侯颖等[2,3]设计了一个钻有4个小孔的金属板作为校准模板,并通过在一个投影角度下得到投影数据，利用解析法得出相关参数。此方法前提是需要将模板摆放到旋转台的中心位置，有一定的精度要求。刘晓鹏等[4]提出了利用细琴弦和带豁口的钢尺得到几何参数。Meng[5]和Yang等[6]提出了无模体标定的方法，陈炼等[7]提出了利用一个简单的校正模型得到少量的投影，计算出几何参数的方法，此方法在计算之前运用了一定的假设。李晓晴等[8]提出了平行双丝法来获取几何参数，此方法虽然模体制造简单、计算速度较快，但是此模体求得的参数不全，而且在计算参数时默认探测器无倾斜角和扭转角，实际安装中难以实现。王珏等[9]在点模型求解方法上进行了改进，有效降低了在求解几何参数时对标定模体安装精度的要求。黄秋红等[10]研究了在不考虑成像系统畸变的情况下，静态系统射线源阵列的几何参数标定方法。杨帅和周凌宏等[11,12]分别从图像质量以及成像系统方面研究几何参数标定方法，杨帅等人提出的方法比较耗时，周凌宏等人提出的方法对标定环境因素要求较高。

1 锥束CT系统扫描结构及其关键几何参数定义

锥束CT系统的扫描结构如图1所示，左侧O-XYZ坐标系为平板探测器，中间A-MNL坐标系为待检测物体，右侧S为射线源。将探测器中间行和中间列相交的焦点定义为中心，用右手法则建立O-XYZ坐标系，以转轴为L轴建立A-MNL坐标系，L轴为旋转中心轴。S(sx,sy,sz)定义为射线源焦点的坐标，并定义S在探测器上的投影坐标为P(px,O,pz)。DAO为探测器到旋转中心的距离，DSA为旋转中心到射线源的距离，DSO为射线源到探测器的距离。并且存在射线源主射线SO与旋转轴垂直。理想状态下，投影坐标P(px,O,pz)在O-XYZ坐标系的原点上。主射线SO是L轴和Z轴的公垂线，探测器不存在任何的绕X轴倾斜、绕Z轴扭转以及在XOY平面上的旋转。但是由于安装误差不可避免，制造误差也会导致出现探测器倾斜、扭转以及射线源焦点投影不在探测器中心等情况，这样会造成重建结果出现伪影，直接影响重建结果的精确度。如图2所示，定义α角为探测器绕Z轴旋转的角度，β角为绕X轴旋转的角度，γ角为探测器在XOZ面旋转的角度，ΔX为探测器在X轴方向的误差，ΔZ为探测器在Z轴上的误差，需要求得的参数为DSA、DSO、DAO、α、β、γ、ΔX、ΔZ。

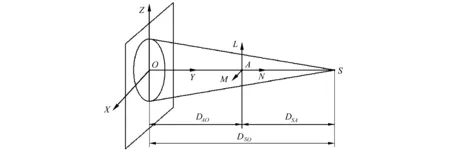
图1 锥束CT系统结构图及其相关几何参数Cone beam CT system structure diagram and the related geometric parameters

图2 探测器安装误差示意图Detector installation error

2 四椭圆法基本原理

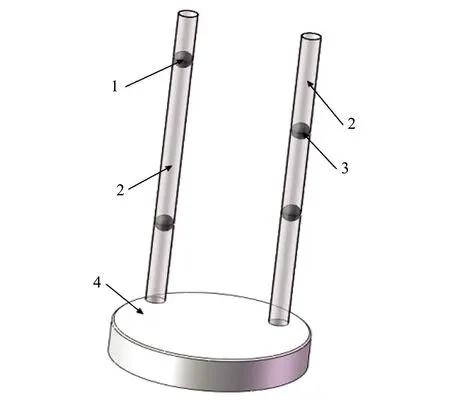
图3 锥束CT系统标定体模三维模型1. 可调节小钢珠，2. 有机玻璃管，3. 固定钢珠，4. 固定底座 Cone beam CT system calibration phantom three-dimensional model1. Adjustable small steel ball, 2. plexiglass tube, 3. fixed steel ball, 4. fixed base

本文中提出的方法是基于圆轨道扫描为假设前提，其使用的标定模体如图3所示，需要两个有机玻璃管(2)，每个有机玻璃管内包含两个直径为2 mm的小钢珠(1)。由于2个有机玻璃管内各有两个小钢珠，钢珠的运动轨迹为4个椭圆，故称为四椭圆法。在设计时，标定模体的2个有机玻璃管应尽量保证与旋转平台垂直，因为其垂直度会影响成像的质量，如果误差较大，会导致计算所得参数误差增大。为保证垂直度要求，文中标定模体设有2个有机玻璃管的固定底座，底座上有2个和有机玻璃管外直径相等的装配孔，装配孔采用基轴制加工，以保证玻璃管与固定底座的垂直度。其次应保证固定底座的平面度，平面度可以用机加工设备来保证。其中一个有机玻璃球管远离旋转中心，另外一个有机玻璃球管离旋转中心距离较近，旋转中心与两有机玻璃球管三者构成不等边三角形，且4个小钢珠中有2个为固定，另外2个为可调节钢珠，适用于任意锥束角不同的锥束CT系统的参数标定。四椭圆法获取全参数的基本思想为：将制成的标定模体放在待测物体转台上，首先把标定模体上2个有机玻璃管旋转到主射线的任意一侧，固定钢珠一端靠近射线源，调节可调节钢珠位置，使4个钢珠在探测器上的投影为2个点，并保证2个有机玻璃管与转台平面垂直，转台旋转一周，获取标定模体360°投影图像，然后对投影图像进行数据处理，计算出需要得到的各个标定参数。

2.1 探测器投影视图参数预处理

(1)

直线AB的长度lAB:

(2)

图4 理想探测器与实际探测器投影轨迹示意图Schematic diagram of the projected path of the ideal detector and the actual detector

直线CD的长度lCD:

(3)

直线AC的长度lAC:

(4)

直线BD的长度lBD:

(5)

2.2 射线源焦点在探测器上投影横坐标ΔX、射线源到探测器的距离DSO的计算方法

本方法所采用的标定体模为双有机玻璃和4个小钢珠所组成，由于2个有机玻璃管分别固定在固定底座相对于旋转中心非对称的不同位置，因此，在标定模体顺时针和逆时针旋转一周时，必定有且仅有2个位置使小钢珠在探测器上运动轨迹相重合。如图5所示，A0代表标定模体的初始位置，θ1和θ2分别表示在两个轨迹投影位置重合时标定模体所旋转的角度。S表示射线源的焦点，A1和A3表示在第一个位置轨迹重合的情况，D1表示在第一个位置重合时X射线源在探测器上形成的坐标，A2和A4表示在第二个位置上轨迹重合的情况，D2表示第二个位置重合时X射线源在探测器上形成的坐标位置。在探测器理想的情况下，A点、D点应与D1点重合，B点、C点应与D2点重合，但是由于安装误差，实际中并不相重合，为了减少计算误差，D1、D2点的横坐标我们分别取投影点A、D和B、C横坐标的平均值。

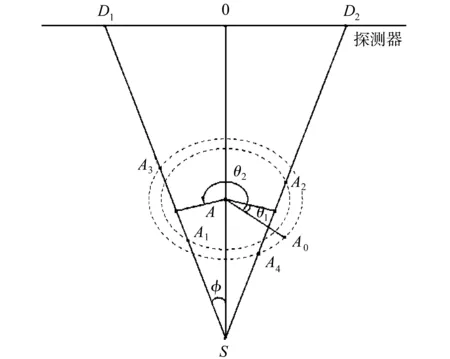
图5 px和Dso的计算模型示意图Schematic diagram of the calculation model of px and Dso

过旋转中心A分别做SD1和SD2的垂线，则几何关系可得：

(6)

(7)

由于初始位置不同，φ角的表达式不同，但是计算思路相同，本文只写出一种情况。

则射线源到平板探测器的距离：

(8)

2.3 探测器的扭转角α、倾斜角β的计算方法

图2中A、B、C、D代表两次投影重合的4个点。由2.2节选取投影位置相重合处，得到侧视图(图6)，由图2空间几何关系得知，直线AB、CD、AC、BD的长度以及倾斜度只与α和β角的大小有关，与其它参数无关。则可令γ=0°，ΔX=0，ΔZ=0。在此关系下推导α和β的表达式，如图6所示，可得以下式：

(9)

(10)

由式(9)和式(10)相除可得到：

(11)

在式(11)中，∠MAS=π/2+∠A′MA-(1/2)∠S，∠AMS=π/2-∠A′MA，∠ADS=π/2-∠A′MA-(1/2)∠S。

其中，∠S可由标定模体中4个小钢珠位置相对关系求出，AD为已知。

图7为俯视图，过M点做ME垂直于SO并交SO于E。在图7中可得如下几何关系：

(12)

(13)

(14)

(15)

由式(14)和式(15)相除可得到：

(16)

A″M=A″S-MS=OS/cosφ-MS

(17)

其中,SO已知，φ和MS已知，则可联立式(11)、式(13)、式(16)、式(17)求得α角，同理可求得β角。

图6 ADS面视图View(seen from ADS)

图7 α角计算示意图Schematic diagram of α angle solution

2.4 探测器在ZOX平面内旋转γ角的计算方法

γ角为探测器在ZOY平面内的旋转角，在本方法所用的模体中，模体旋转一周，得到运动模体运动轨迹参数。在探测器绕p点旋转γ角度时，投影图像如图8所示。实线表示实际投影图形，虚线表示理想投影图形。J、K点分别为上下椭圆的中心为已知，则可由J、K点坐标求得γ角。

(18)

图8 γ角计算示意图Schematic diagram of γ angle solution

2.5 射线源到旋转中心的距离DSA及旋转中心到探测器的距离DAO计算方法

在旋转过程中，标定体模4个小球所确定的平面存在总是两次与锥束主射线垂直，小球在探测器上的投影总存在以下几何关系，如图9所示。

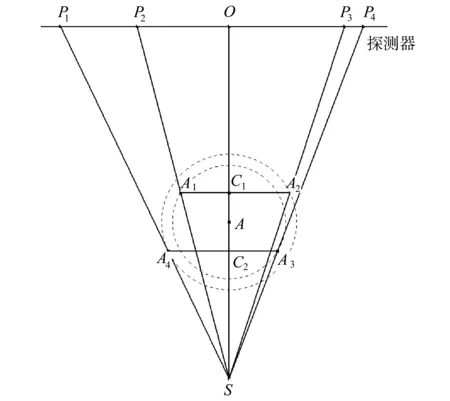
图9 DSA计算模型示意图Schematic diagram of the calculation model of DSA

直线A1A2表示在第一次4个小球确定的平面与折射线垂直时的情况，直线A4A3表示第二次4个小球确定的平面与折射线垂直时的情况。两个小球之间的法向距离为d，其测量实现方法为已知钢珠球的直径为amm，有机玻璃管壁厚bmm。采用数码游标卡尺多次测量2个玻璃管外壁之间的距离，记录测量次数和每次测量值，最后求取平均值x，则d=x-a-2b。OA2=R，OA2=r，则由相似三角形定理可得：

(19)

DAO=DSO-DSA

(20)

2.6射线源焦点在探测器上投影纵坐标ΔZ的计算方法

在2.2中提出，在标定过程中存在两处在不同有机玻璃管的2个小球投影重叠的情况，则以在投影重叠时为基准面建立平面直角坐标系时，可得到图10中的几何关系。

图10 ΔZ计算模型示意图Schematic diagram of the calculation model of ΔZ

Z为旋转中心A在探测器的投影点，C点为过A点到直线SD1的垂足点，根据上图几何关系可知： △SAC≈△SD1Z。

(21)

由上可知需先求出SD1和AC的长度。

(22)

(23)

根据海伦-秦九韶公式可得：

l周长=AA3+A3A1+A1A

(24)

AA3、A3A1、A1A均可由标定模体位置关系得出：S△A3AA1=

(25)

(26)

由式(24)、式(25)可求得AC的长，由式(22)、式(26)可求得SD1的长，由式(21)可以求得D1Z的长。则：

(27)

3 标定结果实验验证

为了验证本方法求得几何参数的准确性，制作了标定模体，并在锥束CT系统上进行了相关实验验证。为了更精确拟合椭圆轨迹参数，小钢珠的直径不宜选择太小，本文中小钢珠采用直径为2 mm的钢球。实验平台主要器材及参数为：X射线源采用东芝E7242X型X射线球管，最大电压为125 kV，角度为14°。平板探测器采用VARIAN PaxScan2520型数字影像探测器，有效面积为250 mm×250 mm，像元矩阵为1536×1920，单个像素尺寸为127 μm。旋转中心台由日本SANMOTION生产的R2AA08075FXP11W型交流伺服电动机和SYNTEC生产的CNC Controller数控系统构成。

3.1 具体实验操作方案

1) 把标定模体垂直放置在旋转台上，旋转一定角度，使两个有机玻璃管位于主射线的同一侧，固定位置钢珠所在的有机玻璃管靠近X射线源一侧，然后调整标定模体，使两个不同有机玻璃管内的小钢珠投影重合。标定体模调整结束，开始标定。

2) 使旋转台顺时针和逆时针旋转一周，得到4个小球的运动轨迹。根据文中提到的计算方法拟合椭圆参数方程，并计算出4个相应的交点坐标。

3) 记录旋转台旋转到两次投影重合时的角度，计算相应的ΔX和射线源到探测器之间的距离DSO。

4)根据文中计算α、β、γ的方法，计算出结果，并校准α、β、γ的角度。

5)记录4个小钢珠所在的平面与探测器平行时，标定体模上4个小钢珠的投影横坐标，并计算射线源到旋转中心的距离DSA以及旋转中心到探测器的距离DAO。

6)在小钢珠投影重合时根据几何关系，计算出最后一个几何参数ΔZ。

图11为搭建的实验平台。

图11 实验平台实物图Experimental platform

3.2 实验结果

从表1中可知，由本文中提到的基于四椭圆锥束CT系统几何参数的算法得出来的计算值与设计时的真实值相比较，求得的全参数误差相对很小，满足实际的应用需求。

为了验证本方法的实际效果，利用河南科技大第一附属医院实际人体口腔数据进行重建，其重建算法为圆轨迹滤波反投影FDK重建算法，重建过程为：1)对得到的投影数据进行加权预处理，即对得到投影数据与滤波函数进行卷积操作；2)把预处理过的数据进行一维的斜坡滤波；3)对滤波后的数据做锥形束的加权反投影。图12和图13为校正前和校正后重建的图像，从图中可以看出校正前图像环影较重，而且细节处模糊不清，轮廓处有伪影。校正后伪影基本消除，清晰度较高。为了更直观地分析结果，计算出了两个图像的峰值信噪比。其计算流程为：1)把两个重建的图像分别导入MATLAB中，并添加相同的椒盐噪声；2)生成系统预定义的3×3滤波器对两张添加噪声的图像进行均值滤波；3)求得两张图像的均值误差MSE；4)求得两张图像的峰值信噪比PSNR。最后求得参数未校正图像的峰值信噪比为11.0487，参数校正后图像的峰值信噪比为14.0413。显然参数校正后得到的图像比未校正得到的图像质量更好，可满足正常医用的要求。

表1 实际几何参数与计算几何参数比较

图12 参数未校正重建的图像Image reconstructed with uncorrected parameter

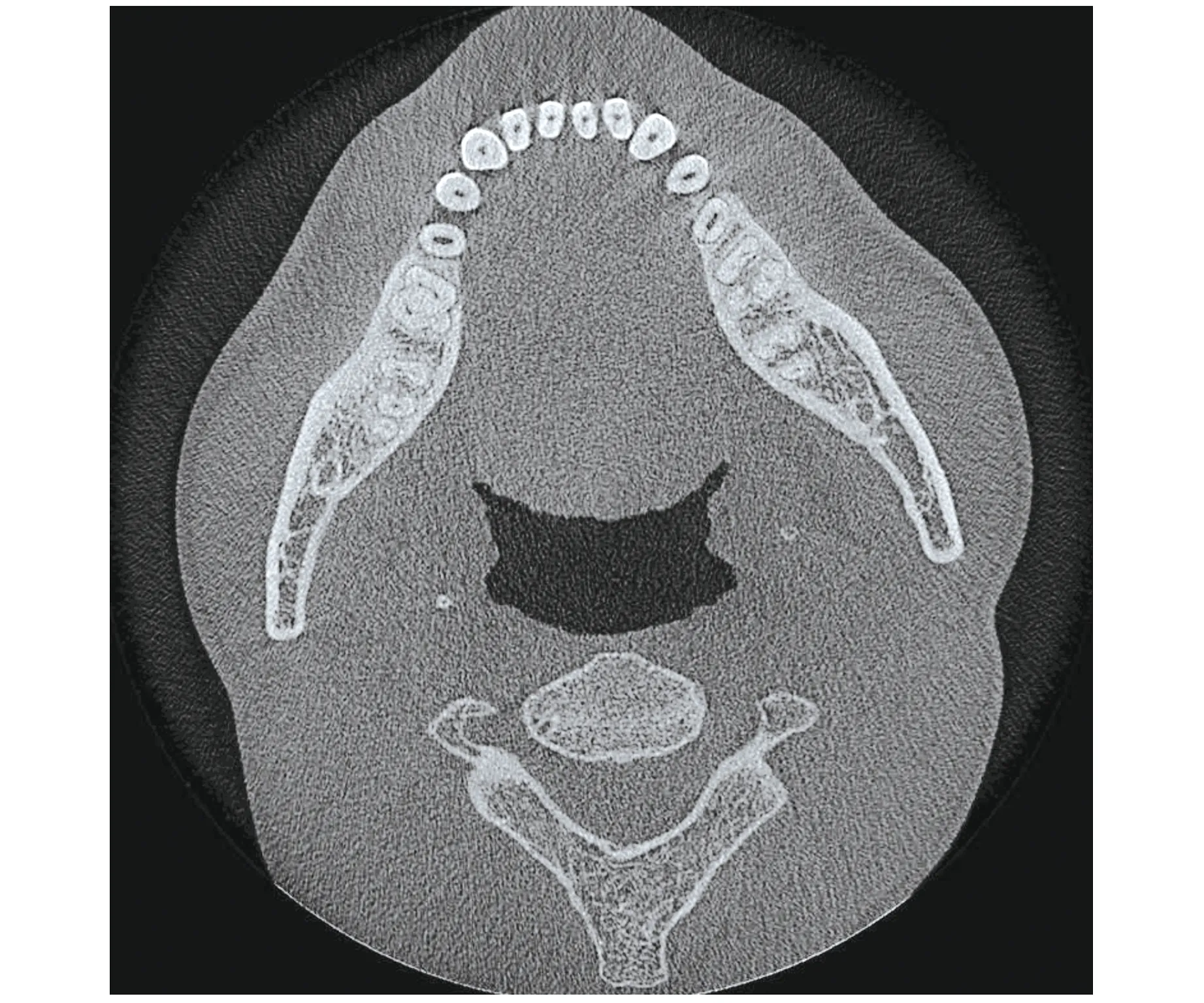
图13 本文方法参数校正之后重建的图像Image reconstructed after parameter correction in this paper

4 结论

基于小球的椭圆轨迹法以及平行双丝法，本文设计了一种通用标定模体并提出基于本标定模体的几何全参数解析算法，从成像敏感参数出发环环相扣，得到的几何参数比较精确。改善了目前标定方法在解析计算标定过程中标定模体的单一性、标定参数不全、参数获取过程中计算较为复杂等缺点。本文设计的这种可调节的通用标定模体，可以适用于任意不同锥角的几何参数标定。在标定前只需要相应调整标定模体，标定过程中，通过简单的几何数学模型，即可获取锥束X-CT系统中的几何参数。实验结果表明，该方法对标定锥束CT系统几何参数是有效的，使用的标定模体通用性强、结构简单，适用于各种CT参数标定。但是目前使用该方法存在一个前提：标定前需要调整模体，使两个小钢珠投影相重合，这一条件是非常难以精确满足的。因此今后我们将进一步研究如何得到一种与标定体模初始状态无关的几何参数标定方法。