基于经典蚁群优化算法求解TSP问题研究

王文明，赵江东，李泽彬

(皖西学院 皖创机器人创客实验室，安徽 六安 237012)

20世纪90年代初，受自然界中真实蚁群集体行为的启发，意大利学者Dorigo等人首次提出了一种基于种群进化的启发式随机搜索算法——蚂蚁系统(Ant System，AS)，它是第一个蚁群优化(Ant Colony Optimization，ACO)算法，并将其成功地用于解决旅行商问题[1]。蚂蚁系统算法具有并发性、正反馈和较好的鲁棒性等优点[2-3]。在蚂蚁系统算法求解问题的过程中，多个蚂蚁同时构建路径，体现了算法的并发性。蚂蚁构建路径的过程中同时释放信息素，在较优的路径上积累的信息素越多，则会吸引更多的蚂蚁集中在这条路径上，进而释放更多的信息素，表现出算法的正反馈调节作用。此外，不会因为单个蚂蚁寻找较差的路径而影响整个算法探索最优解的性能，体现了算法较强的鲁棒性。

1 蚂蚁系统

蚂蚁系统是对大自然中真实蚂蚁行为的一种抽象[4]，模拟了自然界中蚂蚁的觅食行为。蚂蚁系统主要包括两个部分，分别是蚂蚁路径构建和信息素更新。

1.1 路径构建

在蚂蚁系统中，蚂蚁一开始被随机分布在各个城市中。在构建路径即蚂蚁下一步所要访问的城市，将按照随机比例规则对下一个城市进行选择。

(1)

其中，τij(t)是t时刻路径(i,j)上的信息素量；ηij(t)是路径(i,j)上的启发量，表示蚂蚁从城市i到城市j的期望程度，通常取两城市间距离的倒数ηij(t)=1/dij，dij表示城市i到城市j的欧式距离。参数α是信息素因子，参数β是启发式因子，分别表示信息素和启发量的相对重要程度。allowedk表示蚂蚁k在t时刻位于城市i下一步可以选择的城市集合[5](P69)。

在路径构建过程中，蚂蚁选择下一个城市的概率由该边上的信息素量τij和启发量ηij共同决定。参数α和β作用：当α=0，表示蚂蚁在选择下一个城市的过程中只与启发量有关，即距离城市i最近的城市被选择的概率最大，这相当于贪婪算法。当β=0，表示蚂蚁选择下一城市由信息素量决定，没有利用启发量，算法很快会陷入停滞状态。

1.2 信息素更新

经过n个时刻，蚂蚁完成一次周游，在路径i到j上的信息素量按下面的规则进行更新：

(4)

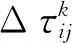
1.3 蚂蚁系统求解TSP问题

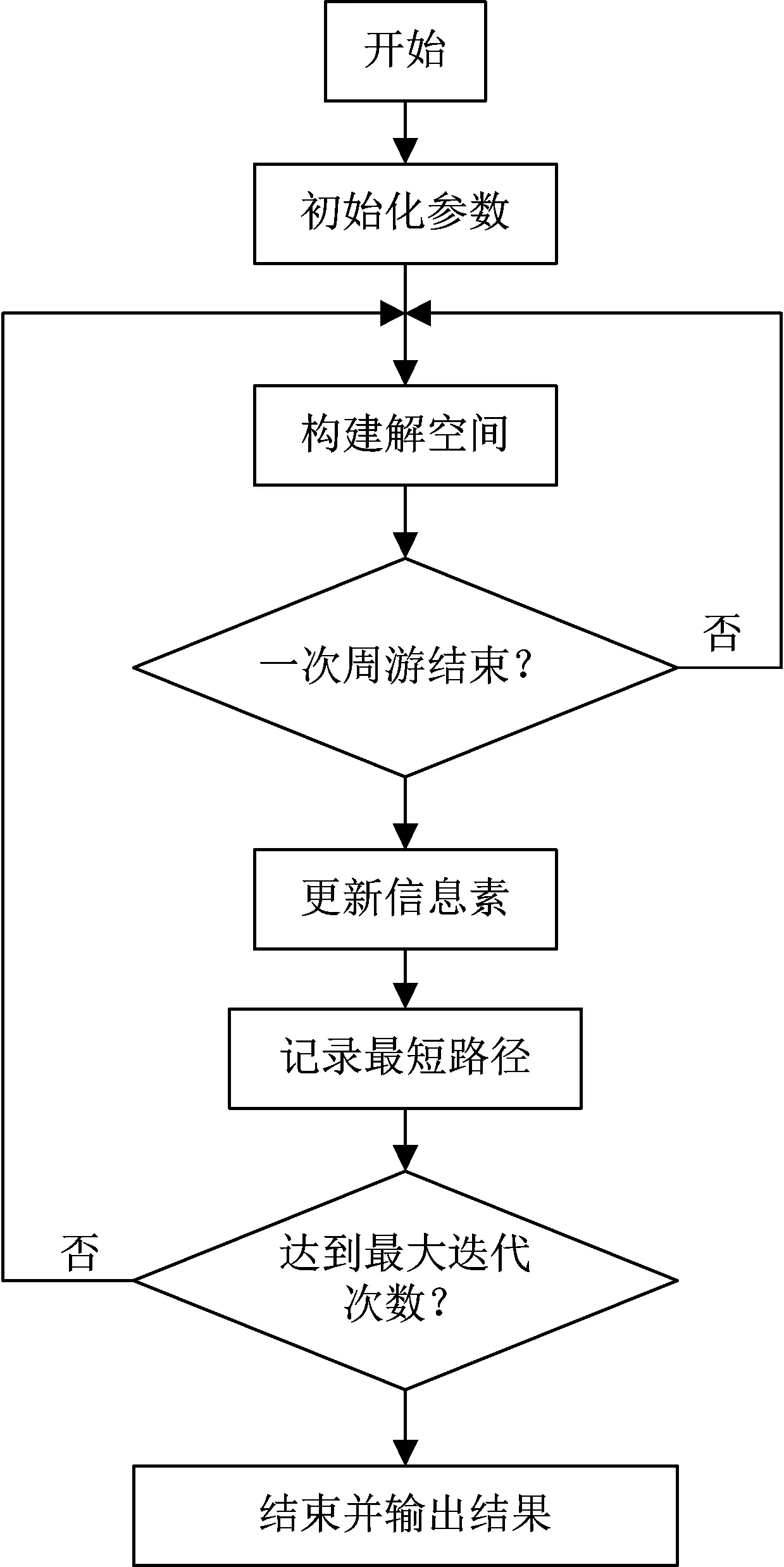
图1 蚂蚁系统求解TSP问题流程图

以TSP问题为例，分析蚂蚁系统求解TSP问题的具体步骤：

Step 1 初始化变量。初始迭代次数Nc=0，最大迭代次数Ncmax，蚂蚁数量m，城市个数n以及各城市坐标，构建启发量矩阵。初始化信息素因子α，启发式因子β，信息素强度Q，路径记录表，信息素矩阵，初始各节点信息素量τij(0)=0，信息素挥发系数等。

Step 2 将m只蚂蚁随机分布在n个城市，并记录它们的起始位置城市，更新各个蚂蚁的路径记录表。

Step 3 构建解空间。m只蚂蚁根据状态转移概率公式(公式1)选择下一个城市，更新路径记录表，完成各自遍历。

Step 4 记录本次迭代中的最佳路线和路径长度。

Step 5 更新信息素。根据公式(2)(3)(4)更新本次迭代后各节点间信息素的量，更新信息素矩阵。

Step 6 达到最大迭代次数，输出结果。

2 经典蚁群优化算法

2.1 精英蚂蚁系统

蚁群算法创始人M Dorigo在AS的论文中也提出了精英蚂蚁系统(elitist ant system, EAS)，EAS算法是对基本AS算法的首次改进[6]。

精英蚂蚁系统的策略是对所有蚂蚁周游的路径中，选择当前最优路径，对其进行增强。将当前最优路径记为Tbs，向当前最优路径添加一种额外的反馈信息。针对当前最优路径Tbs的额外强化是通过向Tbs中的每一条边增加一定量的信息素决定的。其信息素更新策略为：

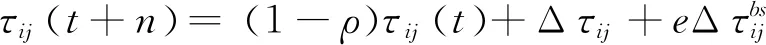
(5)

(6)

其中，e表示精英蚂蚁的个数，Lbs是当前最优路径的长度，(i,j)是当前最优路径上的节点。

EAS算法和AS算法只在信息素的更新方式上有所不同，与AS算法相比较，EAS算法增加了对最优路径的强化作用，在信息素更新时加强了对全局最优解的利用，加强了全局最优蚂蚁对后续蚂蚁的影响，使蚂蚁在当前最优的路径上进行进一步开发，提高了算法的收敛速度[7]。

2.2 排序蚂蚁系统

精英蚂蚁系统有一个缺陷：在路径构建的过程中，使用精英策略导致更多的蚂蚁集中在局部最优区域，使得搜索过程更可能会集中到局部最优解的附近，使得某一条路径上的信息素急剧增加，严重影响了后续蚂蚁解的多样性，造成算法早熟，从而阻止了全局最优解的进一步探索。

基于EAS算法的不足，Bernd Bullnheimer等人提出了基于排序的蚂蚁系统(Rank based Ant System，RAS)算法[8]。当蚂蚁生成一条路径后，将根据它们构建出来的路径长度按递增的顺序进行排列，蚂蚁将要释放的信息素量将根据其排名进行加权。在每一次迭代中，只有排列在前μ只蚂蚁才允许释放信息素。RAS算法的信息素更新规则为：

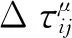
2.3 蚁群系统

蚁群系统(Ant Colony System，ACS)算法增加了新的机制用于改善蚂蚁系统算法的性能[9]。蚁群系统与AS算法的不同之处主要体现在3个方面。第一，状态转移规则不同，在选择下一座城市时，既利用问题的先验知识，又可以进行倾向性地探索。第二，全局信息素更新只应用于最优路径上。第三，加入了信息素局部更新规则。

在ACS算法中，蚂蚁根据伪随机比例选择规则选择城市j作为下一访问的城市。在i城市的蚂蚁k，以概率q0移动到城市μ，其中μ为使τiu(t)*[ηiu]β达到最大值的城市。在ACS算法中，蚂蚁的状态转移公式为：

(9)

其中，j是编号为k的蚂蚁所选的下一节点，q是均匀分布在区间[0,1]中的随机变量，q0(0≤q0≤1)是一个可调参数，allowedk表示可选节点的集合。J是根据式(1)给出的状态转移规则产生出来的一个随机变量。参数q0的大小决定了利用先验知识与探索新路径的相对重要程度。

2.3.2 全局信息素更新

在ACS算法中，只有全局最优的蚂蚁才被允许释放信息素，即全局最优路径上才有信息素量地增加。ACS算法的信息素更新规则为：

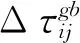
全局信息素更新操作之后，只有位于当前最优路径上的信息素得到加强，并对下一代蚂蚁造成影响。因此，它使得后续蚂蚁继续探索这条最优路径，进而使得算法的收敛速度大大提高，并且使算法在找到一条最优路径之后会持续地选择这条路径直到更优的路径出现。

2.3.3 局部信息素更新

在构建路径的过程中，蚂蚁根据局部信息素更新规则对它所经过的路径进行局部信息素更新[10]，[11](P33)。蚂蚁经过路径(i,j)时：

所有人全愣住了，因为只有武成龙想到唯有萧飞羽应战，这不仅是萧飞羽提示他才悟出了盘龙剑法可以融合整套剑法之威的一招，而且他还想到了萧飞羽独战荒原十狼的故事，特别是昔年九大高手的僧、道、尼联手也只与荒原十狼战成平手！

(12)

局部信息素更新规则避免了精英蚂蚁系统中出现局部最优解的情况，相当于引入负反馈机制，实现信息素的局部调节，增加了蚂蚁探索新路径的机会，避免算法早熟，提高了算法的多样性。

2.4 最大最小蚂蚁系统

德国学者Thoams Stutzle和Holegr Hoos提出的最大最小蚂蚁系统(Max-Min Ant System，MMAS[12])也是性能最好的蚁群优化算法之一，MMAS也是AS的重要扩展版本。MMAS在AS算法的基础上引入了4项主要改进机制，分别是信息素更新，信息素限制，初始信息素设置和信息素重新初始化。

2.4.1 信息素更新

MMAS算法在每代蚂蚁完成周游后进行信息素更新。更新过程分为两步，第一步是每一只蚂蚁走过的路径进行信息素挥发，第二步是在最优路径上进行信息素强化操作[13]。信息素更新过程为：

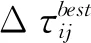
2.4.2 信息素限制

随着各路径上信息素更新，会出现一条路径上的信息素量明显高于其他路径的情况。为避免这种情况发生，通过限制信息素量，可以避免算法在运行过程中路径的信息素量相差过大，从而防止算法出现早熟的现象。在MMAS算法中，任何一条路径上存放的信息素量都被限制在由上界τmax和下界τmin限定的一个范围内。

其中，信息素上界是随着当前最优解的变化而变化的。Pbest表示一只蚂蚁构建当前最优解的概率，实验结果表明，一般情况下Pbest=0.05时能得到较好的结果[14]。

2.4.3 信息素的初始化和平滑处理

随着算法的执行，各路径上的信息素之间的差异缓慢增加，某些路径会被弱化，出现局部收敛的情况。为了增加蚂蚁探索新路径的可能性，当算法出现停滞状态或者在指定次数的迭代中未能得到一条更优的路径时，对信息素进行平滑处理实现信息素重新初始化。

(18)

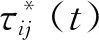
3 仿真实验与结果分析

为了对比分析经典蚁群优化算法的性能特点，本文以TSP问题为例，采用Matlab R2016a软件针对AS，EAS，RAS，ACS，MMAS五种经典蚁群优化算法进行了仿真实验分析。计算机采用AMD处理器，主频2.0 GHz，8 G内存，Windows10操作系统。测试算例选择TSPLIB测试库中的实验问题作为实验对象。所有实验都进行600次迭代，得到5种经典蚁群优化算法在实验中的最优解(如表1所示)，并以kroA100为例得到最短距离与平均距离随迭代次数变化的曲线图(如图2所示)。

参数设置如下：n是城市数目，蚂蚁数量m=n，α=1，β=5，ρ=0.02，Q=100，最大迭代次数iter_max=600。

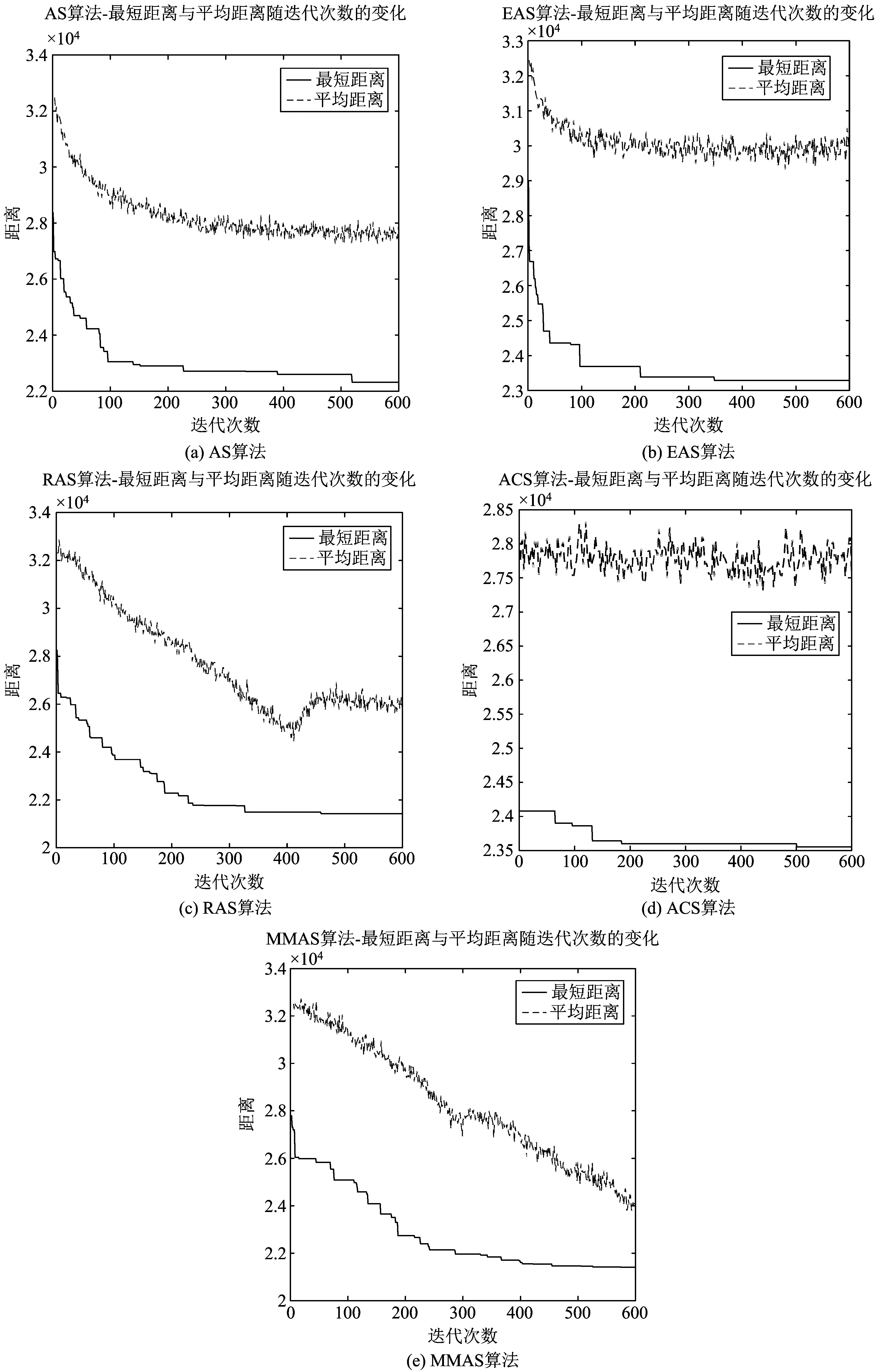
图2 最短距离与平均距离随迭代次数变化

蚂蚁系统算法主要包括路径构建(状态转移规则)、信息素更新、启发式信息构建，三大部分。其中，启发式信息是一种局部信息，在初始阶段可以快速地指导蚂蚁构建较好的解，提高算法在前期的搜索效率。信息素更新策略影响后续蚂蚁地搜索方向，合理地控制信息素可以很好地指导蚂蚁寻找最优解。状态转移规则将先验知识和探索新路径的能力相结合，增加蚂蚁地探索能力以便获得全局最优解。后续经典蚁群优化算法主要在状态转移规则和信息素更新策略上进行改进和优化，分析经典蚁群优化算法，这为后续算法地优化提供了思路。

4 结语

本文主要从解决TSP问题的角度出发，先后分别阐述蚂蚁系统的提出和经典蚁群优化算法，分析了各自算法的改进优化方式，通过研究总结了蚁群算法的发展历程和实现思想，为今后进一步地研究提供了借鉴和参考。最后以典型的TSP问题为例，使用TSPLIB 测试库中的实验问题作为研究对象，并通过MATLAB对经典蚁群优化算法进行了仿真实验。