基于最小二乘修正的混合HS和DY共轭梯度法

陈 贞 晶

(重庆师范大学数学科学学院， 重庆 401331)

共轭梯度法是求解大规模无约束优化问题的最有效的方法之一，具有所需存储量小、强收敛性和计算方便等优点。比如考虑无约束优化问题 minf(x),x∈Rn，共轭梯度法的一般迭代格式为：

xk+1=xk+αkdk

(1)

d0=-g0,dk+1=-gk+1+βkdk

(2)

其中：αk是通过某种线搜索获得的步长，αk>0；dk+1是搜索方向；g(x)是目标函数f(x)的梯度，gk+1=▽f(xk+1)；βk是共轭梯度参数，简称CG参数。不同的βk值，对应不同的共轭梯度方法。

常用的线搜索有很多，我们在这里只考虑Wolfe线搜索：

f(xk+αkdk)-f(xk)≤δαk▽f(xk)Tdk

(3)

▽f(xk+αkdk)Tdk≥σ▽f(xk)Tdk

(4)

其中，0<δ<σ<1。

Hestenes-Stiefel(简称“HS”)方法和Dai-Yuan(简称“DY”)方法都是经典的共轭梯度方法，其参数[1]如下：

HS方法在非精确线搜索下不能保证收敛性，可能无限循环，且不趋近于任何一个解点，但数值计算效果较好。DY方法具有强收敛性，但由于在计算时会受干扰现象的影响，计算效果不佳[2]。

1 HCG方法的修正

1.1 HCG方法

2008年，Neculai Andrei基于拟牛顿方向满足割线条件，提出了混合的HS和DY方法[2]，简称HCG方法。其CG参数如下：

其中

割线方程为Bk+1sk=yk。

HCG方法的计算效果不是很好，不如经典的HS方法。

1.2 ZZL方法

2015年，Saman Babaie-Kafaki和Reza Ghanbari[2]基于HCG方法，采用最小二乘思想，将HCG方法的搜索方向逼近三项共轭梯度法方向[3]之间，极小化后，获得混合参数θk新的取值，即

(5)

其中，三项共轭方向如下所示：

(6)

HCG方法的搜索方向和CG参数如下：

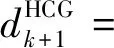
∀k≥0

(7)

(8)

对CG参数进行非负限制，得

这个方法简称HCG+方法。HCG+方法在Wolfe线搜索下全局收敛，计算时间上优于HS和DY 方法。

1.3 EZZL方法

为了减少计算时间，我们采用文献[2]中的最小二乘思想，将ZZL方法替换成带有参数tk的EZZL方法[4]，即

(9)

所以

(10)

其中

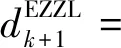
∀k≥0

(11)

tk是一个混合参数。通过对ZZL方法的搜索方向矩阵进行特征值分析，可得参数tk的取值。

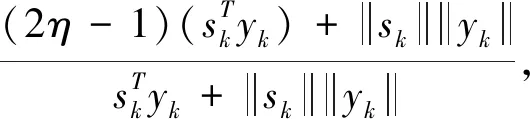
η∈(0,1]

(12)

该扩展的搜索方向，在不依赖任何线搜索和目标函数的凸性下，满足充分下降条件。EZZL方法对一致凸函数全局收敛，且计算上优于ZZL方法。其中，η=0.96。

1.4 HCGQN方法

2018年，Babaie-Kafaki和Ghanbari基于HS方法和无记忆BFGS方法的线性组合，提出了一个新的混合的方法[5]，简称HCGQN方法。其中，无记忆BFGS校正形式为：

其搜索方向如下：

(13)

当目标函数是一致凸函数时，满足充分下降条件。

对上述的搜索方向引入一个基于最小二乘技巧求解的混合参数θk，则式(13)可以写成如下形式：

其中

通过求解下列最小二乘问题，获得混合参数θk。

(14)

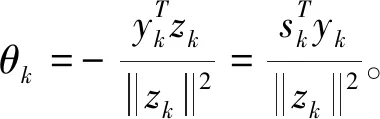
(15)

其中，ξ是一个很小的正数。在数值计算上，HCGQN方法胜过HS和ZZL方法，ξ=10-7。

1.5 MHCG方法

为了减少计算所用的时间，利用文献[2]中采用HCG方法逼近一个充分下降的三项共轭梯度法的思想，将HCG方法[1]逼近一个带有参数的三项共轭梯度法EZZL[4]，使得计算效果优于HCG方法。对混合共轭梯度方法采用极小化最小二乘问题来求解参数θk。

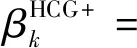
θk∈[0,1]

(16)

通过将HCG方法的搜索方向与EZZL方法的搜索方向的距离之差极小化，可得

(17)

所以有

(18)

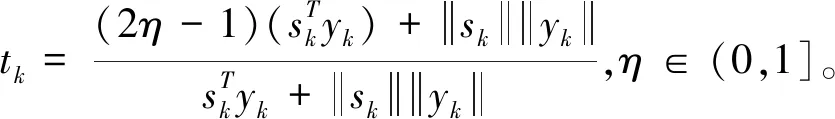
MHCG方法的计算步骤如下：

Step1: 初始化x0∈Rn，且0<δ<σ<1，令k:=0。

Step3: 通过式(2)(12)(16)(18)计算下降方向dk+1。

Step4: 步长αk由式(3)(4)决定。

Step5: 令xk+1=xk+αkdk。

Step6: 令k:=k+1，且转入Step2。

2 MHCG方法的收敛性

在证明收敛性之前，先给出目标函数的两个基本假设和一些重要的引理、定理。

2.1 基本假设

对目标函数进行以下基本假设[2]。

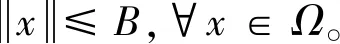
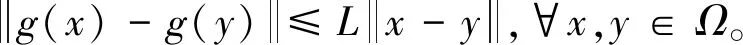
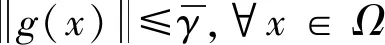
(19)

2.2 引理

[引理1](充分下降条件) 考虑迭代方法如式(1)(2)，CG参数如式(16)，混合参数θk如式(18)，tk的取值如式(12)，在Wolfe线搜索下，搜索方向dk+1满足充分下降条件。

(20)

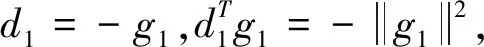
当k≥1时

因此，有

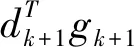
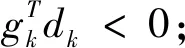
(21)

由引理1，可得

2.3 收敛性证明

下面，证明MHCG方法满足性质(*)。

性质(*)：考虑由式(1)(2)产生的共轭梯度法MHCG，假设

(22)

在假设A、B下，我们说MHCG方法满足性质(*)，如果存在常数b>1和λ>0，使得对任意的k有

|βk|≤b

(23)

且

(24)

[引理3][2]若条件A、B成立，考虑迭代方法即式(1)(2)满足下面3个性质：

(i)βk≥0,∀k≥0

(ii) 步长αk由式(3)(4)得到，搜索方向dk满足充分下降条件即式(20)和Zoutendijk条件即式(21)。

(iii) 性质(*)成立，则有

(25)

接下来，证明MHCG方法的全局收敛性。先给出目标函数f(x)是一致凸函数的等价定义。

等价定义[7]：f(x)是一个一致凸函数。如果存在一个常数μ>0，使得

∀x,y∈Ω

(26)

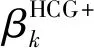
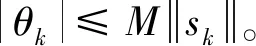
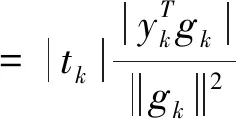
由一致凸函数的等价定义，可得

由假设B(梯度函数g是Lipschitz连续的)和式(19)，可得

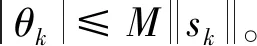
由式(4)，可得

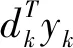
因为θk∈[0,1]，则有

(27)

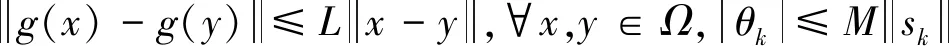
(28)

3 计算效果比较

Hager和Zhang在2005年提出了一个具有充分下降性的共轭梯度方法[7]，简称HZ方法。其参数如下：

截断形式：

Dai和Kou在2013年提出了一个共轭参数[8]：

截断形式：

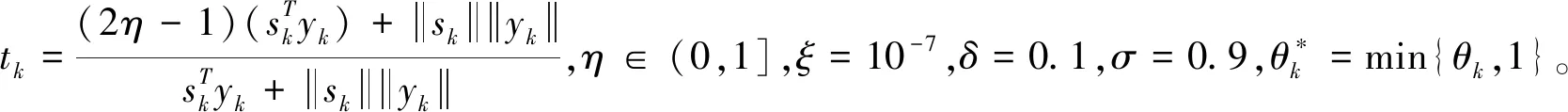
采用以下方式来比较3种共轭梯度方法的有效性。

首先，定义如下比率。

其中：Ncpu,i(EM(j))表示方法j解第i个问题所用的CPU时间；Ncpu,i(EM(1))表示第1个方法解第i个问题所用的CPU时间。

当第1个方法能解问题i0，而第j0个方法不能解问题i0时，

ri0(EM(j0))=max{ri0(EM(j0)):(i0,j0)∉P1}，

其中，S1={{i0,j0}:方法j0能解决问题i}。

当第1个方法不能解问题i0，而第j0个方法能解问题i0时，ri0(EM(j0))=min{ri0(EM(j0)):(i0,j0)∉P1}。

当第1个方法和第j0个方法都不能解问题i0时，ri0(EM(j0))=1。

用这些比率的几何平均数作为算法的最终比值，即

其中：P是测试问题的集合；|P|是测试问题集中测试问题的个数。显然，比值越小，算法的数值计算效果越好。

其次，采用文献[9]提供的方式，绘制各方法的性能曲线，以直观比较各方法的计算效果。

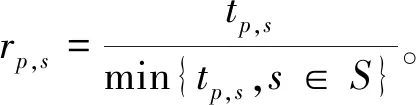
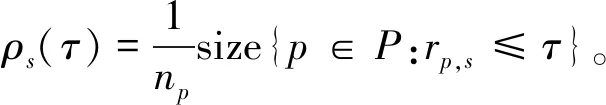
计算结果见表1。其中，NI表示方法的迭代次数，NF表示函数值计算次数，NG表示梯度值计算次数，T表示所用的CPU时间。以HZ+方法的计算用时、迭代次数、函数值计算次数和梯度值计算次数为基准，将其单位化，均用1表示。

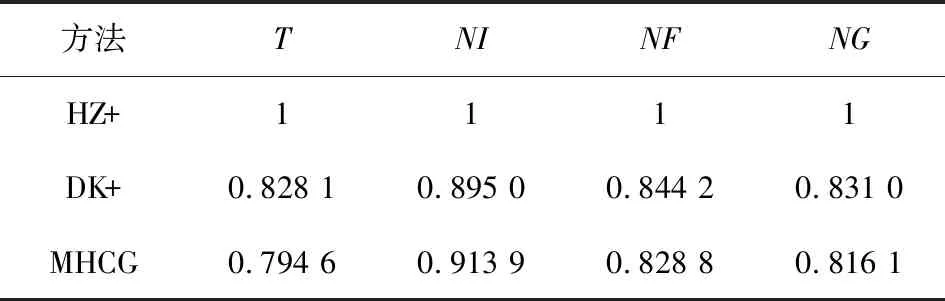
表1 测试结果比较

图1至图4展示了 HZ+、DK+ 和MHCG这3种方法在解决测试问题时表现出的性能差异。在计算时间上，MHCG方法的计算用时最少，所以MHCG方法优于 HZ+、DK+方法。

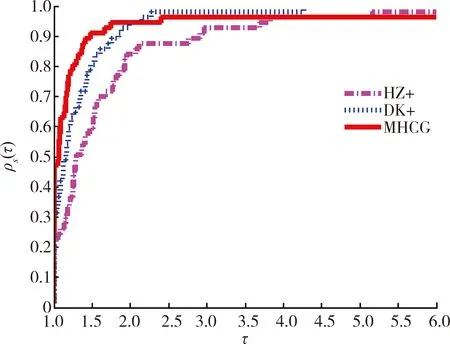
图1 计算用时比较

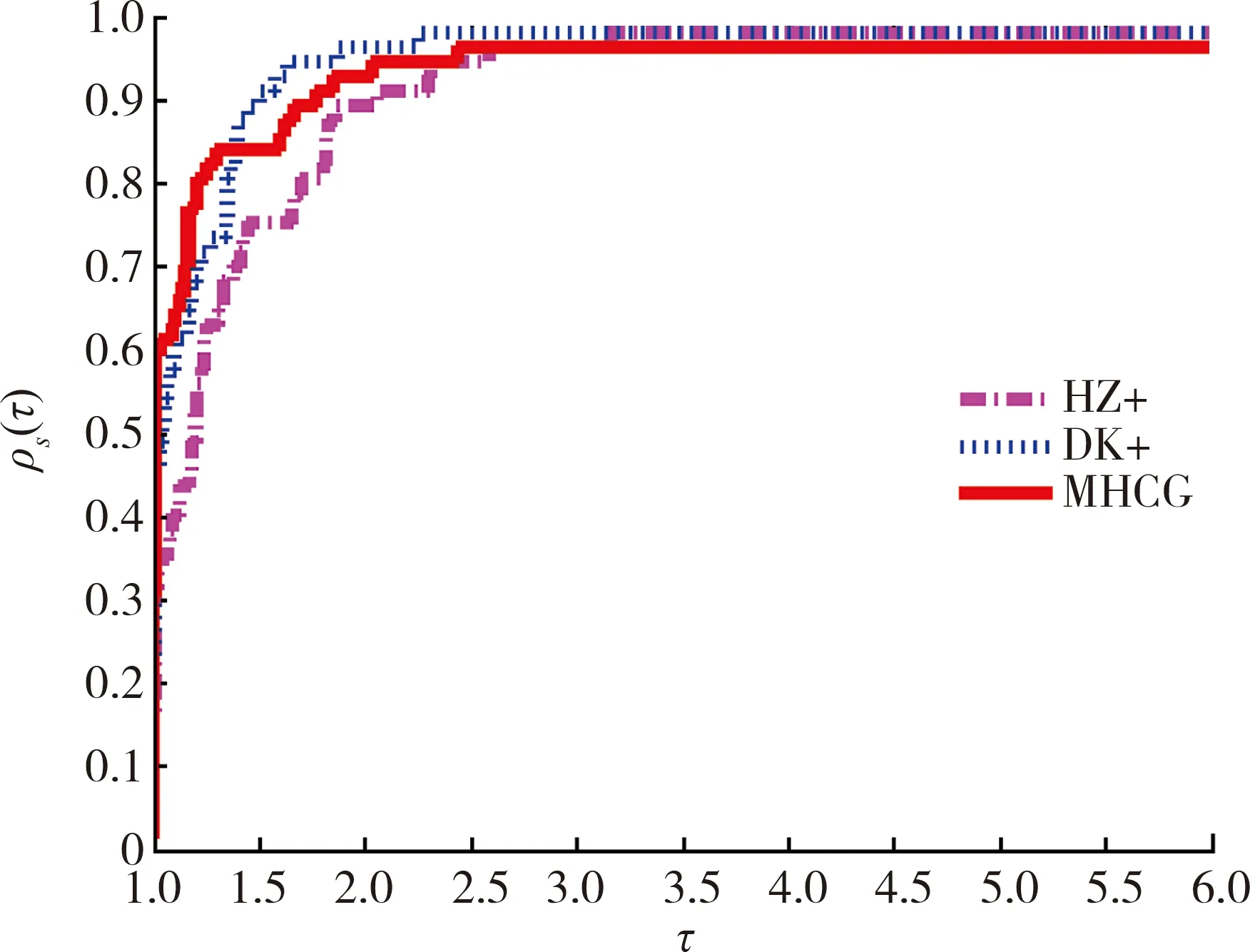
图2 函数迭代次数比较

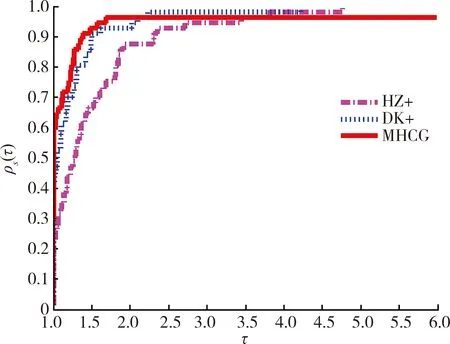
图3 函数计算次数比较

4 结 语

通过对HCG方法逼近一种新的带参数的三项共轭梯度法(EZZL方法)，采用最小二乘的思想，通过极小化混合的方法和充分下降的三项共轭梯度法的搜索方向之间的距离之差，得到新的混合参数θk。从理论上证明了修正后的HCG方法(即MHCG方法)在Wolfe线搜索下满足充分下降性，且对一致凸函数全局收敛。运用HZ+、DK+方法和MHCG方法计算了测试函数库中的59个问题，比较其计算性能差异。结果表明，MHCG方法在计算时间上优于 HZ+、DK+方法。

图4 梯度计算次数比较