随机变量分布函数计算的问题转化方法
杨高翔 吴航航
(安康学院数学与统计学院, 陕西 安康 725000)
在随机变量分布函数一节的教学中,发现许多学生都难以理解分布函数的概念,在计算随机变量分布函数时感到无从下手。为帮助学生克服学习难点,文献[1— 4]已从不同的方面就分布函数的教学问题进行了探讨。下面,针对随机变量分布函数的计算问题,再介绍一种问题转化方法。
关于随机变量分布函数,教材[5]给出的定义是:设X为随机变量,则下面这个函数就是X的分布函数。
F(x)=P(X≤x),x∈(-∞,+∞)
上述定义不仅包含了对离散型随机变量统计规律的描述,也包含对连续型随机变量统计规律的描述。
1 离散型随机变量分布函数的问题转化
设离散型随机变量X的分布律如下,求X的分布函数F(x)。

X-1012P0.20.10.30.4
将问题转化为:已知X=-1,0,1,2,且x∈(-∞,+∞),求满足不等式X≤x的X值有哪些。
【分析】 对于转化后的问题,要得到满足不等式X≤x的X值有哪些,则需讨论x的取值情况。
当x<-1时,满足不等式X≤x的X值不存在;
当-1≤x<0时,满足不等式X≤x的X值为-1;
当0≤x<1时,满足不等式X≤x的X值为-1,0;
当1≤x<2时,满足不等式X≤x的X值为-1,0,1;
当x≥2时,满足不等式X≤x的X值为-1,0,1,2;
根据上述x的取值情况,结合随机变量X的概率分布律,则容易得到随机变量X的分布函数。
当x<-1时,因满足不等式X≤x的X值不存在,所以X的分布函数为:
F(x)=P(X≤x)=0
当-1≤x<0时,要满足不等式X≤x,则X=-1;所以,X的分布函数为:
F(x)=P(X≤x)=P(X=-1)
当0≤x<1时,要满足不等式X≤x,则X=-1,0;所以,X的分布函数为:
F(x)=P(X≤x)=P(X=-1)+P(X=0)
=0.3
当1≤x<2时,要满足不等式X≤x,则X=-1,0,1;所以,X的分布函数为:
F(x)=P(X≤x)=P(X=-1)+P(X=0)+P(X=1)=0.6
当x≥2时,要满足不等式X≤x,则X=-1,0,1,2;所以,X的分布函数为:
F(x)=P(X≤x)=P(X=-1)+P(X=0)+P(X=1)+P(X=2)=1.0
2 连续型随机变量分布函数的问题转化
设随机变量X的概率密度函数如下,求随机变量X的分布函数F(x)。

将问题转化为:已知函数f(t)在(-∞,+∞)上的表达式如下,求函数f(t)在(-∞,x)上的表达式,其中x∈R。
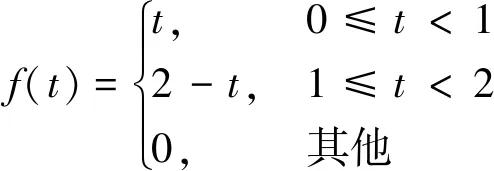
【分析】 对于转化后的问题,要得到函数f(t)在(-∞,x)上的表达式,同样需要讨论x的取值情况。
当x<0时,函数f(t)在(-∞,x)上的表达式为:
f(t)=0,t∈(-∞,x)
当0≤x<1时,函数f(t)在(-∞,x)上的表达式为:

当1≤x<2时,函数f(t)在(-∞,x)上的表达式为:

当x≥2时,函数f(t)在(-∞,x)上的表达式为:

根据上述表达式,可非常容易地得到随机变量X的分布函数。
当x<0时,随机变量X的分布函数为:
当0≤x<1时,随机变量X的分布函数为:
当1≤x<2时,随机变量X的分布函数为:

当x≥2时,随机变量X的分布函数为:

把离散型随机变量的分布函数计算问题,转化为主要讨论满足一类不等式的取值问题;把连续型随机变量的分布函数计算问题,转化为主要讨论已知函数在负半无穷区间上的表达式问题。通过这种问题转化,计算随机变量分布函数的问题就由难变易了。

