高职数学信息化教学模式研究

吕扬

摘 要：本文围绕一元函数的建立来阐述高职数学教学中运用信息化教学手段的全过程，帮助学生直观生动地理解函数关系的建立，解决传统教学中不能解决的难点问题，进一步确定未来高职数学线上线下混合式教育的发展趋势。

关键词：信息化教学;MATLAB软件;几何画板;教学模式

引言

函数是刻画事物间对应关系的重要桥梁，在生活中应用广泛。可是，大部分学生却认为，函数除了考试以外没有什么用。虽然他们已经学过函数的概念，但是对函数的建立和应用理解还不深刻。本文从学生课前反馈的问题入手，以建立一元函数的步骤为主线，围绕两种类型展开：一是根据两事物间确定的对应法则量化一元函数;二是根据两事物的样本数据拟合一元函数。在量化函数过程中，教师运用微课视频、几何画板等信息化教学手段帮助学生直观感受生活中两事物之间的函数关系。在拟合函数过程中，教师指导学生借助MATLAB軟件对样本数据进行拟合，解决传统教学无法解决的问题。

一、信息化教学模式[1]

信息化教学模式，是以现代教学理念为指导，以信息技术为支持，应用现代教学方法，提高教学质量和效率的教学模式。在教学中，教师成为学生主动获取信息的帮助者、促进者;学生变为信息加工的主体、知识意义的主动建构者，信息所携带的知识是学生主动建构意义的对象（客体）;教学过程转变为通过情景创设、问题探究、协商学习、意义建构等以学生为主体的过程;媒体作用也转变为学生主动学习、协作式探索、意义建构、解决实际问题的认知工具，学生用此来查询资料、搜索信息、进行协作学习和会话交流。

二、信息化教学模式的实施

（一）教学目标及重难点分析

本课教学主题是《揭示两事物间的对应关系——建立生活中的一元函数》。授课对象是大一高职学生，他们在第一学期已经学习函数的概念和初步掌握MATLAB软件的操作，但是对函数的建立和应用理解还不深刻。根据课程标准、人才培养方案和学情分析，确定本课的教学目标。知识目标是理解一元函数的概念;掌握一元函数的建立和应用。能力目标是能够根据两事物间确定的对应法则建立一元函数;能够根据两事物的样本数据建立一元函数。素养目标是强化用数学眼光看待事物的意识;提高应用数学知识解决实际问题的能力;形成独立思考、团队合作、精益求精的匠人品质。结合三维目标，本课的教学重点为：一元函数的建立和应用;教学难点是根据生活中两事物的样本数据建立一元函数。

（二）教学实施过程

1.课前导预习

（1）课前，教师活动：教师在学习通上发布小组学习任务。

任务1：预习课中即将学习的三个生活中的函数案例，并完成相应习题。

案例1[2] 少称了多少鸡蛋？

一天，闫老师提着篮子（ 篮子重0.5斤）去集市买10斤鸡蛋。当闫老师往篮子里捡称好的鸡蛋时，感觉比过去买10斤鸡蛋时个数少很多，于是她将鸡蛋装进篮子再让摊主一起称共称得10.55斤，她即刻要求摊主补给少称部分的蛋。请你算一算应补多少斤鸡蛋？

案例2  的士的行驶距离

某市出租车收费标准如下：起步价为8元，起步里程为3 km（不超过3 km按起步价付费）;超过3 km但不超过8 km时，超过部分按每千米2.15元收费;超过8 km时，超过部分按每千米2.85元收费，另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元，求出租车行驶的距离。

案例3[3] 脐橙的需求函数

某地对脐橙的价格浮动与相应的需求量做调查，得到如下数据：

根据以上数据，建立脐橙的需求函数。

习题1[4] （单选题）下列关系中的两个量成正比例关系的是（   ）

A、 从甲地到乙地，所用的时间和速度。

B、 正方形的面积和边长

C、 买同样的作业本所花费的钱数和作业本的数量

D、 人的体重和身高

习题2[5] （单选题）某市为鼓励节约用水，采用分段计费的方法来收取每户家庭的水费，月用水量不超过20m3，按2元/m3收费，超过20m3，超出部分按2.6元/m3。设每户的月家庭用水量为x，应交的水费为y，若小明家六月份交水费42.6元，则小明家该月所用的水量为（）

A、20m3    B、 21m3    C、 22m3    D、 23m3

习题3[6] 某厂节能降耗技术改造后，生产甲产品的产量x（吨）和相应的生产能耗y（吨标准煤）的几组对照数据为下图：

则根据上表数据，y关于x的方程为（）

A、        B、

C、        D、

任务2：每组学生调查收集一个生活中的函数案例。（以其中的三组案例为例）

案例1 一家庭（父亲、母亲和孩子们）计划去某地旅游，甲旅行社说：“如果父亲买全票一张，其余人可享受半票优待”;乙旅行社说：“家庭旅行算集体票，按原价的2/3优惠”。假设这两家旅行社的原价均为3000元/人，试就家庭里不同的孩子数，分别计算两家旅行社的收费（建立表达式），并讨论哪家旅行社更优惠。

案例2 江西省将居民用户用电量以年为周期划分三档，电价分档递增。 第一档为月均180千瓦时及以下，每千瓦时0.60元;第二档为月均181千瓦时至350千瓦时，每千瓦时0.65元;第三档为月均350千瓦时以上。每千瓦时0.90元。试写出每户每月用电量x千瓦时与应交电费y元之间的函数解析式。

案例3 身高与体重

通过测量19个成年男性的身高与体重，得到如下数据，试求两者之间的函数关系。

（2）课前，学生活动：接收学习任务，根据要求按时按质完成课前预习，将预习中遇到的疑难问题通过学习通反馈给教师。

（3）经过学习通统计，78%的同学认为案例3中建立脐橙的需求函数比较难，学生完成课前习题平均得分为79分。教师分析学生的答题情况，发现学生对以下三个问题认识不清：

a：两事物之间是否存在函数关系？

b：如果两事物之间的对应法则确定，如何用函数表示？

C：如果两事物之间的对应法则不确定，如何利用样本数据建立函数关系？

2.课中导学习

课中，为了解决三个问题，教师分为定关系、量法则、拟法则、导步骤、促实践五个环节：

（1）定关系——如何判断两事物之间存在函数关系？

教师播放微课视频，引导学生从映射的角度理解函数的概念，即函数是一对一和多对一的映射，而且自变量x不能有剩余，因变量y可以有剩余。把x与y的关系用萝卜籽和萝卜坑的关系来形容，动画效果直观生动，使学生较快掌握判断两事物之间是否存在函数关系的方法。（如图1所示）

（2）量法则——两事物之间的对应法则确定，如何量化呢？

教师选择课前发布的“鸡蛋少秤”和“打的费用”两个案例，指导每组学生按照：案例的提出、分析、解决和拓展应用四个步骤完成计算。在“鸡蛋少秤”案例中，教师运用绕口令游戏（绕口令内容：篮子实重0.5，秤上称出0.55;花生实重1.0，秤上称出1.1;番茄实重2.0，秤上称出2.2;鸡蛋实重有多少，秤上称出10.0？）帮助学生快速理解物品的实际重量与其在秤上的重量的比值是一个定值，为10/11，二者之间是正比例函数关系，从而列出方程，得到结果，并为今后生活中如何判断少秤提供有效做法。

在“打的费用”案例中，的士行驶距离不同，车费计算法则不同，需要建立分段函数。教师引导学生借助几何画板动态演示分段函数图像的形成过程，在图形中直观显示打的费用22.6元位于第三段解析式（见图2），代入后即可算出的士行驶的距离。

（3）拟法则——如果两事物之间的对应法则不确定，如何利用样本数据拟合函数关系？

教师以课前发布的、学生普遍反馈的疑难问题：脐橙的需求函数为例。这是传统手工计算无法解决的问题，也是本课教学的难点。教师指导学生使用MATLAB软件，分成三步走：①初步识别：根据样本数据画出散点图，初步识别脐橙的需求函数曲线是一条直线;（见图3）②曲线拟合：用一次函数曲线对数据进行拟合，计算出系数;③函数曲线检验：画出拟合曲线图和原数据图进行对比（见图4），从而得到脐橙的需求函数为。

（4）导步骤——建立一元函数的一般步骤是什么呢？

教师启发学生利用xmind APP画出建立一元函数一般步骤的思维导图（如图5所示），分享至学习通。各组学生的反馈结果表明：大部分学生已经掌握了建立一元函数的步骤，学会用数学的眼光看待事物间的联系。

（5）促实践

每组学生按照步骤实践操作，完成自选案例的计算，并选派一名小组代表对成果进行展示。随后，教师和其他组同学提出质疑，组内同学回答，根据表现打分。教师对各组完成情况进行点评，提出修改意见。值得一提的是，在曲线拟合这一步骤中不同学生尝试不同的曲线进行拟合（见图6），从而找到拟合精度更优的函数曲线，充分体现学生独立思考、团队合作、精益求精的匠人精神。

3.课后导巩固

（1）课后，教师把2016年全国大学生数学建模竞赛C题简化后作为课后拓展训练题（如图7所示）。学生发现：曲线的次数越高，拟合效果越好，但是函数越复杂。在精度、简便二者之间不知如何抉择？教师凭借多年指导赛事经验和当年阅卷要点，指导学生：在拟合曲线精度通过检验的前提下，曲线越简单应用价值越高，因此选择二次曲线拟合（见图8）：

以赛促教、以赛促学、以赛促用，实现应用数学知识解决实际问题的数学应用素养目标。

（2）教师在学习通上发布课后作业：

习题1[7] 小明骑自行车上学，开始以正常速度匀速行驶，但途中自行车出了故障，只好停下来修车。后车修好之后，怕耽误上课，加快了速度匀速行驶，则小明路程关于时间的函数图像为（  ）

A                              B                         C                          D

习题2[8] 某城市现行出租车收费标准为：乘车不超过3km，收费10元;超过3km，而不超过15km，超过的里程每千米（不足1km按1km计算）加收2元;超过15km，超过的里程每千米（不足1km按1km计）加收3元。则若某乘客付费49元，则该乘客坐了多遠？（   ）

A 19千米    B 20千米    C 21千米    D 22千米

習题3 在考察硝酸钠的可溶性程度中，对一系列不同温度观测它在水中的溶解度，得出下表所示结果：

表4 硝酸钠温度与溶解度样本数据表

则建立温度与溶解度之间的经验公式为：（   ）

A、      B、

C、      D、

（3）经过学习通统计，学生完成课后习题平均得分为95分，通过课前课后习题测试成绩对比，学生对生活中两事物之间函数关系的认识和建立有了显著提高。

（三）教学效果

1.教学评价

（1）全过程评价

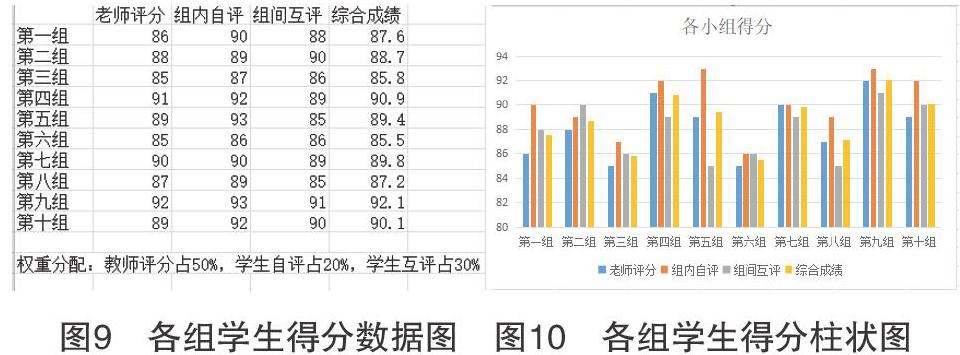
课前课后，学习通测评成绩分别为79分和95分，评价客观有效;课中，教师评分、组内自评、组间互评有机结合，利用权重计算各组综合得分（如图9、图10所示）。

（2）多元化评价

全过程评价、线上线下评价、主观与客观评价的多元化评价方式为量化学生成绩提供科学依据。

2.利用信息化手段取得的教学效果

本课借助MATLAB软件解决传统手工计算无法解决的函数拟合问题，借助视频动画、几何画板软件生动直观地展示教学内容，极大提高了学生的学习兴趣。本课采用情境导入，说身边小事，藏经济哲理，提高学生对数学的亲近感，既达到学以致用的效果，又将课程思政内容潜移默化其中，体现了立德树人的教育思想。

四、结语

本课选取的案例具有代表性，建立一元函数的步骤具有一般性，但是具体问题还需要具体分析。本课教学团队将不断收集生活中、学生专业课中涉及的数学案例，不断完善网络教学平台中的数字资源。本课的教学思路可以推广，探讨极限、导数、积分等数学概念在社会生活中的应用，实现数学为各领域服务的目标。

参考文献

[1] https：//baike.baidu.com/item/%E4%BF%A1%E6%81%AF%E5%8C%96%E6%95%99%E5%AD%A6/8639795.

[2] 宋自奋.高等数学（财经类）[M].江西：江西高校出版社，2018.

[3] 何先应.实用经济数学[M].北京：高等教育出版社，2010.

[4] https：//zhidao.baidu.com/question/937389384639516532.html

[5] https：//zhidao.baidu.com/question/753080758655371964.html

[6] https：//zhidao.baidu.com/question/1830914147443599580.html

[7] https：//zhidao.baidu.com/question/136029048525339045.html

[8] https：//zhidao.baidu.com/question/525557303035111805.html