薄膜体声波谐振器应力负载效应摄动分析
高杨 张大鹏 刘婷婷

摘要:薄膜体声波谐振器(FBAR)力学传感器有很大的应用潜力,但其敏感机理应力负载效应尚不能被准确描述。为准确描述应力负载效应,预测FBAR力学传感器的频率灵敏度,提出一种摄动与有限元联合求解方法,并利用该方法计算FBAR微加速度计的频率一加速度灵敏度。首先,在COMSOL有限元软件中计算FBAR微加速度计在加速度下其压电层AIN的平均偏置应力;接着,在COMSOL中计算单个FBAR的谐振频率与相应的振型;最后,将有限元的计算数据和AIN的材料常数代入摄动积分公式中,得到FBAR微加速度计的频率一加速度灵敏度约为-98.879kHz/g,与文献报道的实验结果-100kHz/g相吻合,验证方法的可行性。
关键词:微加速度计;薄膜体声波谐振器;频率偏移;摄动;有限元
中图分类号:TP212.1;TB931 文献标志码:A 文章编号:1674-5124(2019)09-0001-05
收稿日期:2019-02-21;收到修改稿日期:2019-04-25
基金项目:国家自然科学基金(61574131);四川省教育厅资助科研项目(17ZA0402)
作者简介:高杨(1972-),男,四川绵阳市人,研究员,博士,研究方向为MEMS(微电子机械系统)。
0 引言
随着移动通信技术的发展,薄膜体声波谐振器(thin film bulk acoustic wave resonator,FBAR)便以其高Q值、小体积、可集成化等特点,在射频滤波器应用中得到了飞速发展。在传感检测应用中FBAR也表现出了很大的潜力[1],比如生物化学检测[2-3]、力学检测[4-5]。用于生物化学检测的FBAR传感器依赖于FBAR的质量负载效应,其灵敏度的预测方法由Sauerbrey方程[6]给出。FBAR力学传感器目前主要采用实验测试[4,7-9]的方法,其敏感机理并未被深入研究,且灵敏度的预测方法报道较少。1996年Kosinski[10]在研究晶体谐振器由加速度导致的频率偏移时,将其敏感机理总结为波速的变化和结构尺寸的变化,前者主要是压电体非线性弹性行为,后者主要是线性机械行为。2005年Weber等[11]对FBAR的敏感机理进行进一步探索,涉及压电薄膜厚度的变化、压电薄膜密度的变化和压电薄膜弹性常数的变化。2007年Campanella等[12]提出FBAR的敏感机理可能是电极化效应。2017年赵俊武[13]总结了FBAR力传感器的敏感机理为FBAR的几何结构的改变和FBAR材料性质的改变,并类比于质量负载效应,将FBAR在受到外界应力或应变作用时谐振频率发生偏移的现象命名为应力负载效应。2018年文献[14]验证了在应力负载效应中,电极化效应对谐振频率的影响是可以忽略的。在FBAR应力负载效应中主要是声速的变化,而声速的变化主要是由压电薄膜弹性常数的变化引起的。压电薄膜弹性常数的变化是非线性弹性行为,可以通过摄动积分公式来描述。
本文利用摄动与有限元联合求解的方法,计算了文献[7]报道的一种FBAR微加速度计的频率灵敏度,并将计算结果与文献报道的實验结果对比,验证了该方法的可行性。
1 方法
1.1 摄动积分法
1978年Tiersten[15]给出了摄动积分公式,并利用该公式研究了温度对谐振器的影响[16-17]。之后Kosinski[18]将摄动与结构理论相结合,研究了石英晶体谐振器的加速度灵敏度。摄动法是扰动介质的非线性模型和弹性波机械性质变分分析的结合[19],对于纯弹性非线性的案例:式(1)ω和ωμ分别为扰动后和扰动前压电谐振器的谐振角频率,△μ表示谐振角频率的变化,下标μ表示第μ个特征模态。式(2)Hμ的娜由式(3)给出。式(3)给出的积分公式看起来很复杂,但本质上可以理解为:Hμ表示谐振器在振动模态下随空间变化的有效弹性常数的加权平均值,其权重因子由振动模态的振型决定。gγμ表示对振动模态下实际位移uγμ的归一化振型,压电体的体积为v上标p同样表示第μ个特征模态。ccLγMα被称为弹性常数的偏置系数,△cLγMα为由偏场引起的弹性常数线性变化。式(4)Nμ饰为位移的归一化系数。式(5)中ρ0为压电体的密度。式(6)中cLγJM和cLJMα分别为二阶弹性劲度常数的不同分量(除非特别指出,后文将弹性劲度常数简称为弹性常数),CLγMαAB为三阶弹性常数,sαJKN、sγJKN和SABKN分别为二阶弹性顺度常数的不同分量,δγα为Kronecker张量,TKN1表示压电体受到扰动从而产生的静态偏置应力。
若偏置应力TKN1在压电体内分布是均匀的,可设材料辅因子kLγMαKN和振动模态因子ULγMα分别为:
最后得到由扰动引起的相对频率偏移△μ/ωμ:
因此谐振器频率一偏置应力灵敏度ΓKN可以写为
ΓKN=kLγMαKNULγMα(11)
1.2 摄动与有限元的联合求解
当FBAR传感器受外界载荷时,FBAR受限于安装结构而发生变形,此时FBAR内产生偏置应力,而偏置应力的存在会导致压电薄膜的弹性常数变化。一阶摄动积分公式有效地将含扰动影响的复杂特征值问题式分解为两个相对简单的问题:求解扰动的应力偏置和求解无扰动时的振动问题。因此,采用摄动与有限元联合求解FBAR谐振频率偏移,有限元软件使用COMSOL Multiphysics软件,具体步骤如下:
1)求解FBAR结构的偏置应力。在COMSOL中建立FBAR传感器的结构模型,加载外界载荷并利用稳态分析,得到FBAR结构的偏置应力分布云图。定义压应力为正,拉应力为负。外界载荷可以是加速度、压力或温度。
2)计算FBAR压电层的平均偏置应力。采用平均偏置应力可以简化计算,利用COMSOL中的体平均求解压电层的平均偏置应力,并拟合出外界载荷与平均偏置应力的关系式。
3)求解FBAR的特征模态和特征频率。一般FBAR传感器结构较为复杂,为简化计算,可以建立单个FBAR的结构模型,结构、尺寸和边界条件均与传感器中保持一致,定义FBAR压电层为积分域,使用特征频率分析,得到FBAR纵波模式所对应的特征频率和相应的振型,并计算振动模态因子ULγMα。
4)计算频率一偏置应力灵敏度。根据压电层的弹性常数和平均偏置應力的方向,利用压电材料(AIN)弹性常数与应力的关系,得到的值,并计算材料辅因子kLγMαKN。
5)计算FBAR传感器的频率灵敏度。将振动模态因子和材料辅因子代入式(11)中,得到FBAR的频率灵敏度,再利用拟合的外界载荷一平均偏置应力的关系式,得到FBAR传感器频率一外界载荷的灵敏度。
2 案例计算
本算例的结构模型来自于文献[7]报道的一种FBAR微加速度计。文献并没有给出FBAR微加速度计的全部结构参数,只给出了电极Pt的厚度为0.18μm,压电层厚度为0.7~1μm,FBAR的面积为20×100μm2,谐振频率约为2.7GHz,因此需要通过文献中的扫描电镜照片(SEM)估计FBAR微加速度计的其他结构参数。FBAR微加速度计的结构及尺寸如图1所示,FBAR压电层的厚度为0.7μm,4个支撑梁上的FBAR(底电极Pt-压电层AIN-顶电极Pt)的厚度均为1.06μm。计算过程中所涉及的材料参数如表1所示,AIN的三阶弹性常数[20]如表2所示,表中与后面的计算均使用缩写下标表示。AIN共有10个独立的三阶弹性常数,其他三阶弹性常数均可通过对称关系[21]得到。
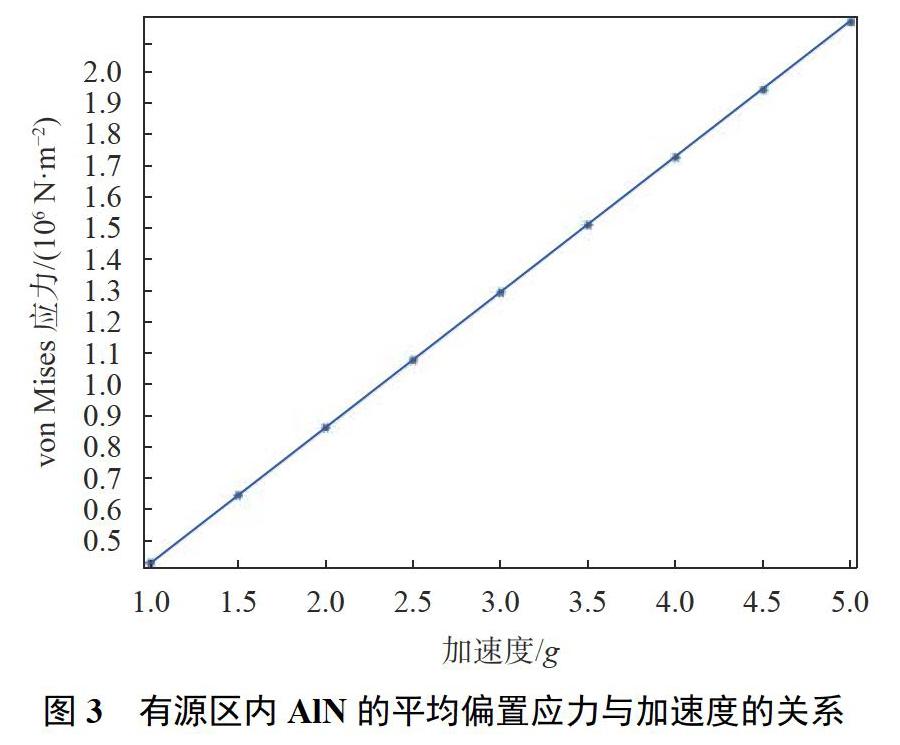
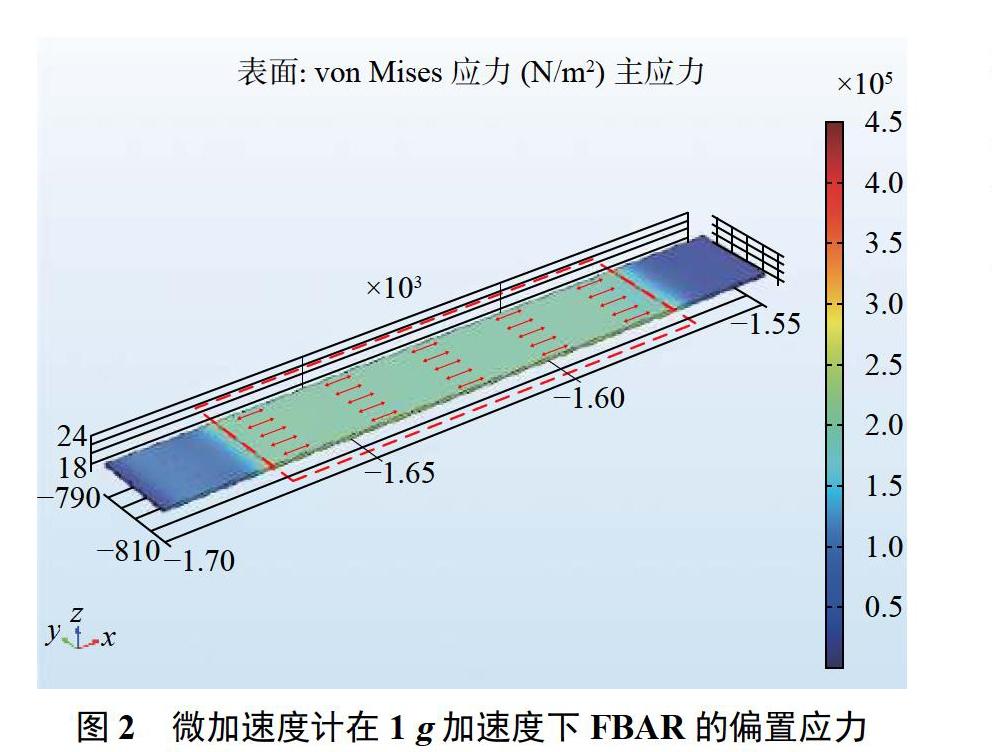
在COMSOL软件中建立FBAR微加速度计的三维模型,并使用固体力学接口。支撑梁一端连接质量块,另一端固定,加速度a3沿z轴负方向作用于质量块。利用稳态分析,计算加速度a3与FBAR偏置应力的关系。当加速度a3=1g(9.8m/s2)时,FBAR的偏置应力(von Mises应力)分布云图如图2所示,图中红色虚线框内FBAR部分为有源区,在有源区内偏置应力分布均匀,红色箭头表示主应力方向,即有源区内偏置应力主要为沿x轴方向的拉应力。其他方向(沿y轴方向和沿z轴方向)的应力远小于沿x轴方向的应力,因此可以忽略。利用稳态分析中的参数化扫描,计算不同加速度下FBAR的偏置应力。再利用体平均,得到有源区内压电层(AIN)沿x轴方向的平均偏置应T11(Pa)与加速度a3(g)的关系,如图3所示。其拟合关系式为:
T11=432.47×103×a3(12)
接下来需要计算FBAR的谐振频率和相应的振型,为简化计算,只需要在COMSOL中建立单个FBAR的三维模型,其结构、尺寸和边界条件均与微加速度计中FBAR保持一致。利用COMSOL中的特征频率分析求解FBAR的谐振频率及其相对应的振型,FBAR的厚度拉伸模态(纵波模式)的振型如图4所示,其谐振频率约为2.3634GHz。定义FBAR有源区内的压电层为积分域,利用体积分计算振动模态因子。由于主要考虑的是纵波模式,因此只需要计算振动模态因子U33=0.01648ppm/kPa。
然后利用AIN的二阶弹性常数,计算得到弹性顺度常数sABLM。当加速度沿z轴方向作用于微加速度计时,FBAR产生的偏置应力主要是沿x轴方向的拉应力,因此平均偏置应力为沿x轴方向的拉应力T11。利用表3中AIN单轴应力P/与弹性常数c33的关系[22]得到。将上述计算结果代入式(8)中,得到FBAR在纵波模式下受沿x轴方向的平均偏置应力T11时,材料辅因子k331=-5.87。
最后将振动模态因子U33和材料辅因子k331代入式(11)中,并利用平均偏置应T11叫与加速度a3的拟合式,得到FBRA频率-加速度灵敏度约为-98.879kHz/g。负号表示谐振频率向下漂移。而文献[7]中微加速度计受到沿z轴负方向的加速度时,FBAR的谐振频率向下偏移。按本文的符号规定,文献[7]报道的实验测试结果应为-100kHz/g。本文计算结果与文献报道的实验测试结果一致。
3 结束语
本文提出一种摄动与有限元联合求解的方法,结合FBAR微加速度的案例,预测了FBAR受到加速度时的频率偏移。首先利用COMSOL中的稳态分析,求解FBAR微加速度计在受到沿z轴负方向的加速度时FBAR的偏置应力。再利用体平均得到压电层AIN的平均偏置应力,并建立平均偏置应力与加速度的拟合关系式。之后利用COMSOL中的特征频率分析,单独求解FBAR的谐振频率和相应的振型,并利用体积分计算振动模态因子。接着根据AIN平均偏置应力的方向,利用AIN弹性常数与应力的关系,计算材料辅因子。最后将振动模态因子和材料辅因子代入摄动积分公式,利用平均偏置应力与加速度的拟合关系式,得到FBAR微加速度计的频率-加速度灵敏度约为-98.879kHz/g,与文献报道的频率-加速度灵敏度-100kHz/g吻合,验证了摄动与有限元联合求解方法的可行性。
参考文献
[1]GAO J N,LIU G R,LI J,et al.Recent developments of filmbulk acoustic resonators[J].Functional Materials Letters,2016,9(3):1630002.
[2]唐宁,常烨,刘晶,等.新M便携式薄膜体声波谐振气体传感器的研制与应用[J].纳米技术与精密工程,2016(5):331-336.
[3]PANG W,ZHAO H,KIM E S,et al.Piezoelectricmicroelectromechanical reson.nt sensors for ch-;cal andbiological detection[J].Lab on a Chip,2012,12(1):29-44.
[4]CHIU K H,CHEN H R,HUANG R S.High-performance filmbulk acoustic wave pressure and temperature sensors[J].Japanese Journal of Applied Physics,2007,46(4):1392-1397.
[5]NAGARAJU M B,LINGLEY A R,SRIDHARAN S,et al.27.4 A 0.8mm 3+0.68 psi single-chip wireless pressure sensorfor TPMS applications[C]//Proc of IEEE International Solid-State Circuits Conference-(ISSCC),2015:1-3.
[6]ZHANG H,KIM E S.Micromachined acoustic resonant masssensor[J].Journal of Microelectromechanical Systems,2005,14(4):699-706.
[7]CAMPANELLA H,PLAZA J A,MONTSERRAT J,et al.High-frequency sensor technologies for inertial force detectionbased on thin-film bulk acoustic wave resonators(FBAR)[J].Microelectronic Engineering,2009,86(4):1254-1257.
[8]CAMPANELLA H,CAMARGO C J,ESTEVE J,et al.Sensitivity of thin-film bulk acoustic resonators(FBAR)tolocalized mechanical forces[J].Journal of Micromechan;csand Microengineering,2013,23(6):065024(10).
[9]DELICADO A,CLEMENT M,OLIVARES J,et al.Influenceof induced stress on AIN-solidly mounted resonators[C]//Procof IEEE European Frequency&Time Forum,2016.
[10]KOSINSKI J A.The fundamental nature of accelerationsensitivity[C]//Proc of IEEE International Frequency ControlSymposium,1996.
[11]WEBER J,LINK M,PRIMIG R,et al.Sensor for ambientpressure and material strains using a thin film bulk acousticresonator[C]//Proc of IEEE Ultrasonics Symposium,2005:1258-1261.
[12]CAMPANELLA H,PLAZA J A,MONTSERRAT J,et al.12E-1 accelerometer based on thin-film bulk acoustic waveresonators[C]//Proc of IEEE Ultrasonics Symposium,2007:1148-1151.
[13]赵俊武.FBAR的应力负载效应研究[D].绵阳:西南科技大学,2017.
[14]张大鹏,高杨,王宇航,等.电极化对FBAR应力负载效应影响的分析[J].压电与声光,2018,40(3):59-62.
[15]TIERSTEN H F.On the nonlinear equations of thermo-electroelasticity[J].International Journal of EngineeringScience,1971,9(7):587-604.
[16]SINHA B K,TIERSTEN H F.First temperature derivatives ofthe fundamental elastic constants of quartz[J].Journal ofApplied Physics,1979,50(4):2732-2740.
[17]SINHA B K,TIERSTEN H F.On the temperature dependenceof the velocity of surface waves in quartz[J].Journal ofApplied Physics,1980,51(9):4659-4665.
[18]KOSINSKI J A.The fundamental nature of accelerationsensitivity[C]//Proc of IEEE International Frequency ControlSymposium,1996.
[19]MASSON J,REINHARDT A,Ballandras S.Simulation ofstressed FBAR thanks to a perturbation method[C]//Proc ofIEEE Mtt-s International Microwave Symposium Digest,2005.
[20]PANDEY D K,SINGH D,YADAV R R.Ultrasonic wavepropagation in IIIrd group nitrides[J].Applied Acoustics,2007,68(7):766-777.
[21]BRUGGER K.Pure modes for elastic waves in crystals[J].Journal of Applied Physics,1965,36(3):759-768.
[22]WANG Z,ZHAO J,GAO Y,et al.First-principle studies onthe influence of anisotropic pressure on the physical propertiesof aluminum nitride[J].Materials Research Express,2017,4(1):016303(8).
(編辑:李刚)

