超立方体Qn在PMC模型下的2-条件诊断度

韩 妙,刘 杰,原 军

(太原科技大学应用科学学院,太原 030024)

随着计算机的普及与发展,计算机系统越来越复杂,形成如今的多处理器系统,虽然多处理器系统在计算等方面有着卓越的优势,但计算机系统发生故障的概率也大大增加。为了保证计算机系统的正常运行,诊断出并替换掉故障处理器就至关重要。故障诊断需要依靠模型的建立,1967年,Preparata等[1]创建了系统级故障诊断理论,提出了一种系统级故障诊断模型——PMC模型。PMC模型是通过相邻两个处理器相互测来试实现故障诊断的。传统的诊断度假定系统的每个结点的所有邻点可能同时发生故障,但从实际角度出发,发生这种事件的概率很小。因此传统诊断度严重低估了系统的自我诊断能力。为改善传统诊断度这一缺点,很多学者提出了新的诊断度。2005年,Lai等[2]提出了条件诊断度的概念,它要求系统中每个结点至少有1个好邻点,并证明了超立方体Qn在PMC模型下的条件诊断度为4(n-2)+1,n≥5.2012年,Peng等[3]提出了g-好邻条件诊断度的概念,它要求系统中每个非故障结点至少有g个好邻点,并证明了超立方体Qn在PMC模型下的g-好邻条件诊断度为2g(n-g)+2g-1,0≤g≤n-3.g-好邻条件诊断度的研究得到了学者的广泛关注,取得了一系列的研究成果,参见文献[3-5].在条件诊断度和g-好邻条件诊断度概念的启发下,我们提出了2-条件诊断度的概念,要求系统中每个结点至少有2个好邻点。本文研究了超立方体Qn在PMC模型下的2-条件诊断度。

1 预备知识

Preparata等[1]提出的PMC模型是通过相邻两个处理器相互测试,即对应到图G中两个处理器为顶点对(u,v),(u,v)表示从u到v进行测试,则u为测试者,v为被测试者。用0和1代表是否出现故障,0代表未出现故障,1代表出现故障。若u为故障点,则测试结果不可靠。系统在PMC模型下的测试过程就是对每对相邻结点进行相互测试,因此系统的测试结果是一个集合,称为G的症候,用σ表示,可以用一个有向图T=(V,L)表示,其中(u,v)∈L代表u和v相邻。所以一个症候σ就是一个函数σ:L→{0,1}.对于给定的症候σ,顶点集F⊆V(G),若症候σ是由顶点集F满足下列情况产生的,则称σ与F一致。

(1) 若u,v∈V(G)-F,则σ(u,v)=0;

(2) 若u∈F,v∈V(G)-F,则σ(u,v)=1;

(3) 若u∈V(G)-F,v∈F,则σ(u,v)=1;

(4) 若u,v∈F,则σ(u,v)=1.

令σ(F)是与F一致的症候的集合。对于G中两个不同的顶点子集F1和F2,如果σ(F1)∩σ(F2)=ø,则称F1和F2是可区分的;否则,称F1和F2是不可区分的。

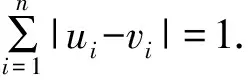
图1 超立方体Q1、Q2、Q3Fig.1 Hypercubes Q1、Q2、Q3

由定义1.1可知,Qn是一个n正则图,Qn中任意两个相邻顶点没有公共邻点。

定义1.2 在一个系统G=(V,E)中,对于任意两个不同的2-条件故障集F1和F2,其中|F1|≤t和|F2|≤t,若F1和F2是可区分的,则G是t-可诊断的。使得G是t-可诊断的最大值t,称为图G的2-条件诊断度,记为t2(G).

引理1.3[7]若k≤n-2,Qk是Qn的一个子图,且CQn(Qk)=NQn(Qk)∪V(Qk),则δ(Qn-CQn(Qk))≥n-2.

引理1.4[4]假设n≥3,且1≤g≤n-1,则κg(Qn)=(n-g)2g.

引理1.5 设H是n维超立方体的子图,H≅Q4且CQn(H)=NQn(H)∪V(H),其中n≥5,那么|NQn(H)|=16(n-4).

证明:令Q4=X40n-4,X∈(0,1).由定义1.1知,

|NQn(Q4)|=|V(X410n-5)∪V(X4010n-6)∪…∪V(X40n-51)|=|V(X410n-5)|+|V(X4010n-6)|+…+|X40n-51|=24(n-4)=16(n-4)

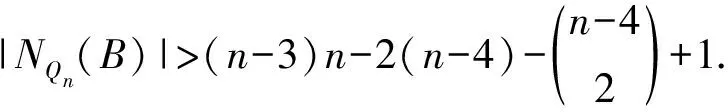
引理1.7[8]设A是Qn中每个点的度至少为g的子图,则当1≤g≤n时,有|V(A)|≥2g.

2 主要结果

DahBura等[9]给出了PMC模型下F1和F2是可区分的充要条件。

引理2.1[10]设F1和F2是G中任意两个不同的顶点子集,则F1和F2是可区分的当且仅当存在一个顶点u∈V(F1∪F2),v∈F1ΔF2,使得(u,v)∈E,如图2所示。

引理2.2是由定义1.2和引理2.1得到PMC模型下2-条件t-可诊断的充要条件。

引理2.2[3]一个系统G=(V,E)在PMC模型下是2-条件t-可诊断的充要条件对于G的任意两个2-条件故障集F1和F2(|F1|≤t,|F2|≤t),存在顶点u∈VF1∪F2,v∈F1ΔF2,使得(u,v)∈E,如图2所示。

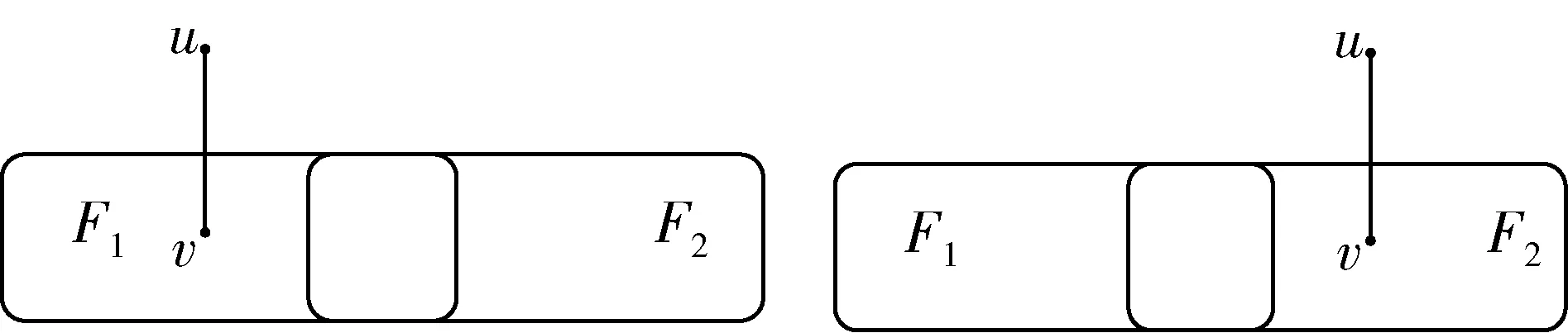
图2 点集对(F1,F2)在PMC模型下可区分Fig.2 A distinguishable pair(F1,F2)under PMC model

首先讨论超立方体Qn在PMC模型下t2(Qn)的上界。

引理2.3 设n≥7,则超立方体Qn在PMC模型下的2-条件诊断度t2(Qn)≤16n-57 .

证明:取超立方体Qn中的一个子图H={A1,A2,B1,B2}≅Q4,其中H1={A1,A2},H2={B1,B2},Ai,Bi≅Q2,i∈{1,2}.图H的构造如下图3所示。我们假设F1=H1∪NQn(H),F2=H2∪NQn(H),F=F1∪F2.

由引理1.5知,

|N(H)|=24(n-4)=16(n-4)

从而

|F1|=16(n-4)+8=16n-56,

|F2|=16(n-4)+8=16n-56

由2条件故障集的定义知,对任意的u∈V(Qn),都有|NQn-F(u)|≥2.不失一般性,假设H≅Q4=X40n-4,下面分三种情形讨论:

情形一:u∈H1∪H2.

不妨设u∈H1,由于H≅Q4,如图3,故|NQn-F1(u)|=|NF2-F1(u)|=2.同理,u∈H2时,|NQn-F2(u)|=|NF1-F2(u)|=2.

情形二:u∈N(H).

易看出NQn(H)=V(X410n-5)∪V(X4010n-6)∪…∪V(X40n-51).不妨设u∈V(X410n-5),令u=u1u2u3u410n-5,则|NH(u)|=1;|NQn[X410n-5](u)|=4,即|NN(H)(u)|=4.因此,当n≥7时,|NQn-F(u)|=n-5≥2.

情形三:u∈V-(F1∪F2).

由引理1.3,当n≥4时,δ(V-F1∪F2)≥n-2≥2.也就是说,|NQn-F(u)|≥n-2≥2.

结合三种情形可得,F1和F2是2-条件故障集。

又因为N(H)⊆F1∩F2,所以对任意u∈F1ΔF2,v∈V(Qn)-(F1∪F2),有(u,v)∉E(Qn).由引理2.1知,F1和F2不可分。再由引理2.2知,超立方体Qn在PMC模型下不是2-条件(16n-56)-可诊断的,即t2(Qn)≤16n-57.引理得证。

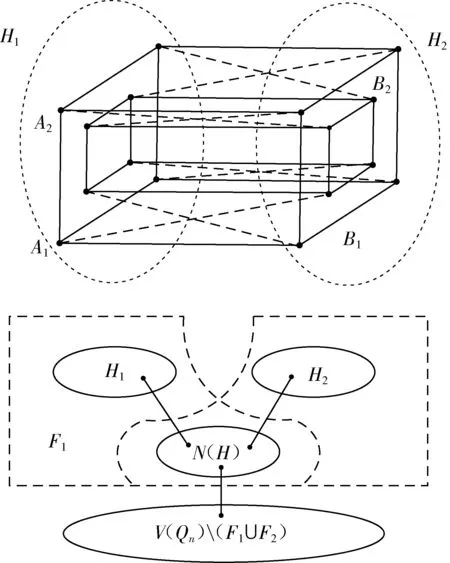
图3 图H及顶点集F1和F2Fig.3 Graph H and vertex sets F1 and F2

下面讨论超立方体Qn在PMC模型下t2(Qn)的下界。

引理2.4 设n≥7,假设超立方体Qn中的任意两个2-条件故障集F1和F2都有F1∩F2是Qn的一个4-好邻割,则超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)≥16n-57.

证明:欲证明t2(Qn)≥16n-57,则只需要证明Qn是2-条件(16n-57)-可诊断的,根据引理2.1和引理2.2,等价于证明V(Qn)中任意两个不同的2-条件故障集F1,F2,其中|F1|≤16n-57,|F2|≤16n-57,存在u∈V(Qn)(F1∪F2),v∈F1ΔF2,使得(u,v)∈E(Qn).采用反证法,假设存在两个不同的2-条件故障集F1,F2(|F1|≤16n-57,|F2|≤16n-57).对于任意的u∈V(Qn)(F1∪F2),v∈F1ΔF2,都有(u,v)∉E(Qn).不失一般性,假设F2F1≠ø,分以下两种情形进行讨论。

情形一:V(Qn)=F1∪F2.

令f(n)=2n-32n+114,则导数f′(n)=n2n-1-32,当n≥5时,f(n)′>0,从而f(n)是一个增函数。故当n≥7时,f(n)>0.即当n≥7时,2n≥32n-114.

另一方面:

2n=|V(Qn)|=|F1|+|F2|-|F1∩F2|≤

|F1|+|F2|=2(16n-57)=32n-114,

矛盾。

情形二:V(Qn)≠F1∪F2.

根据假设V(Qn)(F1∪F2)与F1ΔF2之间没有边,F2ΔF1≠ø且F1和F2是2-条件故障集,可得δ(F1ΔF2)≥4,由引理1.7可知,|F1ΔF2|≥24=16,可知F1-F2和F2-F1中有一个点的个数至少为8,不妨设|F2-F1|≥8.由题设可知F1∩F2是Qn的一个4-好邻割,再由引理1.4知,

|F1∩F2|≥24(n-4)=16n-64.

从而有：

|F2|=|F2-F1|+|F1∩F2|≥

8+16n-64=16n-56.

这与已知条件中的|F2|≤16n-57矛盾。

综上所述,两种情况都产生矛盾,故即当n≥7时,Qn是2-条件(16n-57)-可诊断的,即t2(Qn)≥16n-57.

结合引理2.3和引理2.4可得以下定理:

定理2.5 设n≥7,假设超立方体Qn中的任意两个2-条件故障集F1和F2都有F1∩F2是Qn的一个4-好邻割,则超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)=16n-57.

下面对超立方体Qn在PMC模型下的2-条件诊断度做进一步的讨论。

引理2.6 设n≥61,则超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)≥16n-57.

证明:欲证明t2(Qn)≥16n-57,则只需要证明Qn是2-条件(16n-57)-可诊断的,根据引理2.1和引理2.2,等价于证明V(Qn)中任意两个不同的2-条件故障集F1,F2,其中|F1|≤16n-57,|F2|≤16n-57,存在u∈V(Qn)(F1∪F2),v∈F1ΔF2,使得(u,v)∈E(Qn).采用反证法,假设存在两个不同的2-条件故障集F1,F2,其中|F1|≤16n-57,|F2|≤16n-57.对于任意的u∈V(Qn)(F1∪F2),v∈F1ΔF2,都有(u,v)∉E(Qn).

由引理1.7知,|F1ΔF2|≥24.令V(Qn)-(F1∪F2)=S,则

|S|=|V(Qn)-(F1∪F2)|≥2n-2(16n-57).

由引理2.4情形一知,当n≥7时,|V(Qn)-(F1∪F2)|≥24.由题设可知F1和F2不可分,所以NQn(F1ΔF2)⊆F1∩F2.换言之,Qn[V(Qn)-(F1∩F2)]的每个分支的顶点个数不少于24.令F1ΔF2=B,则|B|≥24,|V(Qn-CQn(B))|≥24.由引理1.6得,

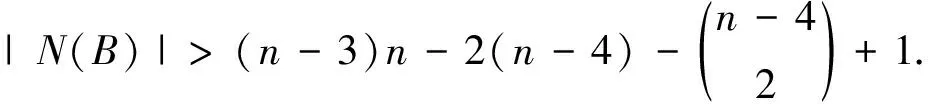
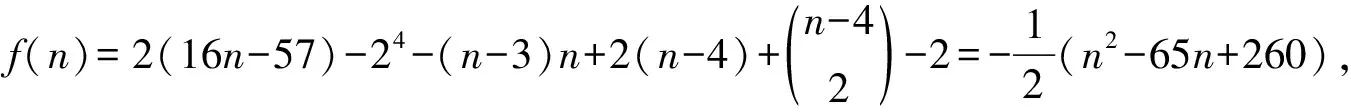
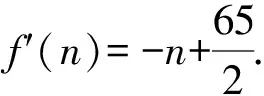
另一方面:

2(16n-57)-24≥|F1|+|F2|-

|F1ΔF2|=|F1∩F2|≥

矛盾。

综上所述,当n≥61时,Qn是2-条件(16n-57)-可诊断的,即t2(Qn)≥16n-57.

结合引理2.3和引理2.6可得以下定理:

定理2.7 设n≥61,则超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)=16n-57.

3 结论

提出了2-条件诊断度的概念,它是条件诊断度概念的一个推广。本文首先证明了:若超立方体Qn中的任意两个2-条件故障集F1和F2都有F1∩F2是Qn的一个4-好邻割,其中n≥7,则超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)=16n-57.进一步,得到当n≥61时,超立方体Qn在PMC模型下的2-条件诊断度:t2(Qn)=16n-57.结果表明,当要求每个结点的非故障邻点至少为2时,超立方体能诊断出故障结点数较条件诊断度有显著提升。