喷水试验机桁杆系统气动优化设计

张锋 宋锐红

摘   要：基于理论估算，CFD分析和风洞试验，在桁杆系统总体布局的基础上，通过优化主桁杆剖面，确定小翼尺寸、安装位置，解决了桁杆系统气动优化设计中的主要参数选择。获得了满足系统需求的总体气动外形，通过飞行试验对设计进行了检验。

关键词：喷水试验机  桁杆剖面  小翼  计算流体力学

中图分类号：V216.8                                文献标识码：A                        文章编号：1674-098X（2019）05（c）-0024-06

结冰飞行试验是飞机定型试飞的高风险科目之一，传统的结冰飞行试验需要苛刻的气象条件，ARJ-21飞机为了适航取证不得不远赴北美进行自然结冰试验，说明我们不具备可控的结冰飞行试验条件。因此，研制不受气象条件限制，可重复使用的结冰喷水试验机，模拟结冰气象微条件，对提升我国军、民机防/除冰设计和定型试飞具有现实意义。

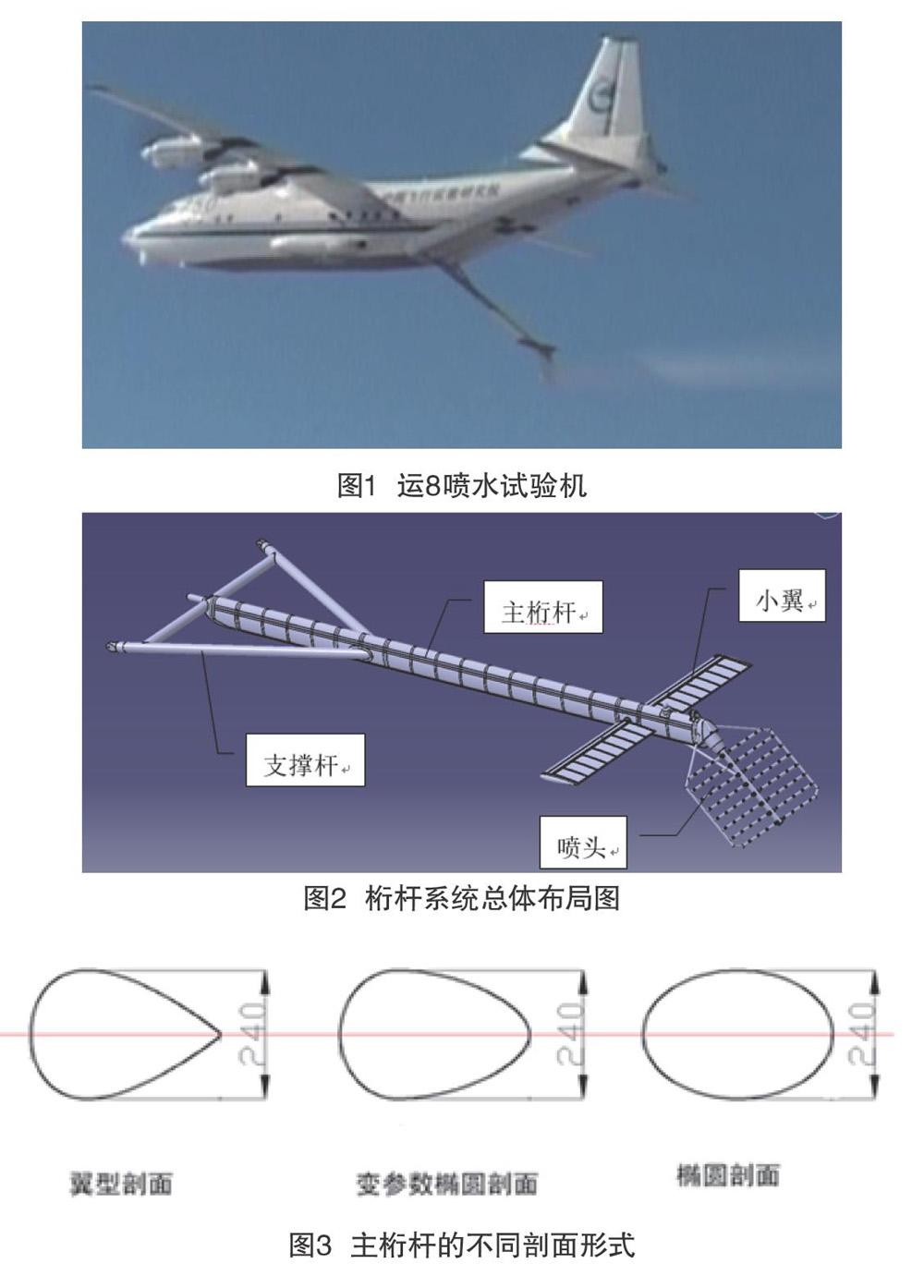
美国在20世纪50年代后期开始研究结冰喷水试验机，距今已成功应用于多种军、民型号飞机的结冰飞行试验和冰风洞的验证试验[1]。本文研究的结冰喷水试验机以运8飞机为载机平台，在舱内加装结冰试验装置，在机身外围加装桁杆系统，通过小翼操纵桁杆系统的纵向运动，待桁杆系统稳定在工作位置后，打开舱内的结冰试验装置，在桁杆系统的喷头后方形成人工模拟结冰微环境，为被试飞机提供结冰试验所需的气象环境，加快型号研制周期，缩减试飞成本，见图1[2]。

在试验机的研制过程中，桁杆系统的气动布局设计不仅关系到桁杆系统能否正常收放，是否满足结冰喷水的试验要求，同时对载机的飞行性能、飞行品质以及飞行安全有着较大的影响，成为改项目研制中的重点难点之一。

1  桁杆系统总体布局设计

喷水试验机桁杆系统为单自由度桁杆系统，主要由主桁杆、支撑杆、喷头和小翼组成，总体布局如图2所示。支撑杆为结构强度设计所附加，喷头为成品件，主桁杆和小翼为本次优化设计的主要对象。经分析，主要设计目标、限制条件和设计参数如下。

1.1 设计目标

（1）桁杆系统对载机的气动特性影响尽可能小;

（2）小翼有足够的操纵效率实现桁杆系统的正常收放;

（3）桁杆系统下放角度30°～40°。

1.2 设计限制

（1）桁杆系统的尺寸、布局应与载机几何协调;

（2）主桁杆剖面厚度不小于240mm，以保证内部管路、线路的空间需求。

1.3 设计参数

（1）主桁杆剖面形状;

（2）小翼尺寸、安装位置。

2  主桁杆剖面优化设计

喷水试验机主桁杆类似硬杆式加油机的加油杆[2]，具有典型的二元特性，其剖面形式的选择不仅决定了整个桁杆的气动特性，而且对载机的飞行性能及品质有着不可忽略的影响。

2.1 待选剖面

椭圆剖面由于具有二阶光顺、保凸性好、结构简单等优点，是飞机整流外形常用的剖面形式，Kwon、Chitta、Benazza等对椭圆翼型升阻特性进行了数值计算研究[3-5]。翼型剖面也是气动整流常用的剖面外形，当此剖面的长细比较小时会产生严重的气流分离，甚至会出现升力线斜率反号的特殊现象[6]。变参数椭圆剖面位于椭圆剖面与翼型剖面之间，由于后缘较饱满，可能具有相对较好的气动特能。

分别选取翼型剖面，变参数椭圆剖面和椭圆剖面进行对比计算分析，其中翼型剖面采用NACA 0070翼型[7];椭圆剖面短轴/长轴比例为0.7;变参数椭圆剖面以30%为最大厚度点，前后分别使用Rho=0.414和0.35的二次曲线衔接而成，最大相对厚度保持70%。三种剖面厚度均为240mm，弦长约340mm，主桁杆长度8300mm，三种剖面形式见图3。

通过CFD计算确定三种剖面桁杆的气动特性。

计算状态：高度H=4km，速度Vb=400km/h

计算构型：主桁杆处于工作位置。

2.2 计算结果

图4为主桁杆处于工作位置时，三种剖面形式的侧力/阻力特性。图5为三种剖面形式的流线图。

椭圆剖面桁杆的侧力随侧滑角的增大明显大于翼型和变参数椭圆剖面，这对单自由度喷水试验机设计而言，对整个桁杆系统的结构设计非常不利;主桁杆在工作位置时，椭圆剖面桁杆的阻力最大，翼型剖面次之，变参数椭圆剖面桁杆的阻力最小;无侧滑时翼型、变参数椭圆和椭圆剖面的气流分离点分别在55%、75%和80%弦长，变参数椭圆剖面具有较小的气流分离区，产生振动的风险相对较小。

在剖面弦长和厚度相同的基础上，椭圆剖面、变参数椭圆剖面相对翼型剖面，其截面积和有效厚度有不同程度的增加，对于结构设计有利。

综合以上分析，变参数椭圆剖面具有综合较优的气动和结构特性，可作为主桁杆剖面的优先選项。

3  小翼尺寸及位置设计

小翼控制桁杆系统的收放运动，经分析，在桁杆系统的收放过程中，当桁杆系统处于工作位置时，在气动力的作用下，桁杆系统产生一个较大的上升旋转力矩，需要小翼产生足够的负升力来平衡该上升力矩。这就要求小翼拥有足够的舵效，来实现桁杆系统的正常收放。

3.1 小翼舵效研究

小翼舵效主要由其升力和安装位置决定，小翼的升力通过桁杆作用在桁杆系统的转轴处，产生旋转力矩，以操纵桁杆系统的收放。同飞机俯仰力矩规定，小翼产生使飞机抬头，桁杆系统下放的力矩为正。经分析研究，公式（1）为小翼相对桁杆系统转轴的舵面效率，由于升力产生使桁杆系统上收的力矩，故公式（1）为负值。

（1）

其中：CLa小翼的升力线斜率;

ρ小翼处的密度（对于低速不可压流动，）;

kq小翼区域速度阻滞系数;

小翼的面积;

L小翼25%气动弦长距离桁杆系统转轴的距离;

θ桁杆系统下放角度，θ=-18°～40°;

S机翼参考面积;

Ca机翼平均气动弦长;

小翼为三维翼面，其流动特性不同于翼型剖面，存在展向流动，升力系数可通过公式（2）进行估算。

（2）

其中：小翼翼型的升力线斜率;

AR小翼展弦比，AR=4.5;

e效率因子，其典型值0.6～0.95之间，此处取0.8。

3.2 小翼尺寸及位置设计

经CFD计算，在低速情况下，无小翼的桁杆系统处于工作位置（约35°）时，其旋转力矩系数大约为-0.015，若平衡该力矩所需小翼的偏角为10°，则小翼的设计舵效应为-0.0015。

假设小翼采用经典的NA0012翼型，展弦比AR=4.5，展长b∈（1.5～3m），距离桁杆系统转轴长度L∈（5～8m），根据公式（1），估算各种组合情况下小翼舵效如图6所示。根据图6的理论估算值，综合考虑小翼舵效和桁杆系统结构设计的相容性，取展长b=2.8m，弦长c=0.6m，安装位置L=7.25m，作为小翼尺寸及位置的初始设计值，此时小翼舵效约为-0.0015。

4  CFD计算分析

4.1 计算模型

为减小网格量，提高计算效率，计算模型采用半模形式，计算网格采用非结构网格，各网格模型均采用相同的参数设置，生成10层棱柱网格模拟飞机和桁杆系统的附面层，飞机第一层附面层网格高度为飞机平均气动弦长的10-4量级，桁杆系统第一层附面层网格高度为小翼平均气动弦长的10-4量级，相邻两层附面层厚度的比例为1.2，网格量大约为750万。

桁杆系统模拟5个下放角度，分别为-18°，-9°，0°，20°，40°，在每个角度下，小翼角度分别设置为±12°，±6°，0°，共生成25套网格，图7为桁杆系统下放角度θ=0°，小翼偏角δw=0°时的网格模型。

4.2 计算结果

图8为飞行Ma=0.5，桁杆系统不同下沉角度时，其俯仰力矩系数随小翼偏角的变化曲线。由计算结果可知：

（1）桁杆系统在不同角度下，其俯仰力矩系数随小翼偏角的增加而较小，桁杆系统稳定性较好。

（2）桁杆系统在-18°～20°的范围内，小翼有足够的效率操纵桁杆系统。

（3）假设小翼的失速迎角为15°，通过外插延伸，可知该小翼可使桁杆系统最大下放到约-35°。

（4）当桁杆系统在收起状态（θ=18°），小翼δw=-18°时，由于机身干扰，小翼上翼面处的流道变窄，小翼上翼面的压力增量小于自由流中的理论增量，致使此时小翼的负升力增量小于自由流中的理论增量，这一负升力增量的减小降低了桁杆系统的旋转力矩系数。

（5）当桁桿系统平行与机身水平线（θ=0°）时，由于机身干扰使小翼处的气流产生较大的上洗，增加了此处小翼的实际迎角，当δw=12°时，小翼上翼面出现气流分离，此时升力增量小于自由流中的理论升力增量，使得此时桁杆系统的旋转力矩系数增量减小。图9为此时小翼上翼面气流的分离情况。

5  风洞试验验证

5.1 试验方法

为保证试验数据的准确可信，模型采用反装“增量法”安装。反装可避免风洞支架对桁杆系统的干扰，使飞机腹部及桁杆系统处在无干扰影响的气流中。“增量法”可避免整体模型支架扣除的误差、模型其它方面带来的误差及试验数据全量的修正误差。

流场观察试验采用“丝线法”。

试验风速：测力试验v≈70m/s，流场观察试验v≈40m/s。

试验雷诺数：Re≈1.02×106。

模型支撑方式：前后两点支撑。

5.2 主桁杆选型

图11为主桁杆选型方案的阻力增量，试验结果表明，桁杆系统下沉21°和42°时，变参数椭圆剖面桁杆相对翼型剖面桁杆减阻0.0007～0.0010，性能较优，与CFD计算分析趋势一致。

5.3 桁杆收放角度试验

（1）桁杆下沉30°，小翼偏角-15°，正常飞行迎角αw=4°～12°时，桁杆系统旋转力矩系数CR>0，并留有适当的余量，可以实现下沉操纵;

（2）根据数据分析，小翼偏角-15°时，桁杆系统能够下沉到36°，所以下沉限制偏角确定为36°。

6  飞行试验问题及解决办法

（1）架次1：锁止机构开锁后，桁杆系统未正常下放。

原因分析：桁杆系统在收起状态，小翼预设角度δw=0°（平行与桁杆系统），根据CFD计算分析，此时桁杆系统的气动合力产生一个使其上收的力矩，在未操纵小翼的情况下，无法实现正常下放。

（2）架次2：桁杆系统正常收放，实现了喷水作业与最大下放角度验证。

2015年12月28日，15：06：48秒，试验机实现了持续约4min的喷水作业，此时桁杆下放角度θ=23°，小翼偏角δw=-13°。

2015年12月28日，15：14：45秒，桁杆系统实现了持续大约20s的最大下沉角度验证，此时桁杆下放角度稳定在θ=32°，小翼偏角δw=-15°。

7  结语

试验机在气动优化设计过程中准确把握了桁杆系统特殊布局的技术特点，通过理论分析、CFD计算和风洞试验相结合的方式，解决了桁杆系统气动优化设计的主要参数选择。主要结论如下。

（1）變参数椭圆剖面具有综合较优的气动和结构特性，选定为主桁杆的剖面形式。

（2）通过理论分析小翼舵效、结合CFD计算，确定了小翼的尺寸及位置。

（3）通过CFD计算和风洞试验，分析验证了桁杆剖面的选型和桁杆系统的收放特性，为桁杆系统的飞行控制设计提供原始数据输入。

（4）通过飞行试验验证了桁杆系统的设计，为进一步发展三自由度的喷水试验机奠定了坚实的基础。

参考文献

[1] Russell A. Ashenden， Conducting Artificial Tailplane Icing Evaluations at the Air Force Flight Test Center， AIAA-95-0450 33rd Aerospace Sciences Meeting and Exhibit， January 9-12，1995/Reno， NV.

[2] Jeremy J.Simth*， Donald L.Kunz. Simulation of the dynamically coupled KC-135 Tanker and refueling boom. AIAA Modeling and Simulation Technologies Conference and Exhibit 20-23， August 2007.

[3] Kwon J， Choi S. Aerodynamic characteristics of elliptic airfoil at high Reynolds number[J]. Journal of Aircraft，2008，45（2）：641-650.

[4] Chitta V， Dhakal T P， Walters D K. Prediction of aerodynamic characteristics for elliptic airfoils in unmanned aerial vehicle applications， Low Reynolds number aerodynamics and transition， Genc MS（ED.）， 2012，InTech.

[5] Benazza A， Blance E， Abidat M. 2D Detached-eddy simulation around elliptic airfoil at high Reynolds number[J]. Journal of applied Science， 2011.

[6] Hoerner S F，Borst H V. Fluid-dynamic Lift 2ed[M].1985.

[7] C.H. Spenny. Boom Performance Envelope Expansion for Aerial Refueling With the KC-135 Tanker， AIAA/AHS/ASEE Aerospace Design Conference， February 16-19，1993.