脉冲磁场传感器的设计与灵敏度修正方法

朱宇洁　郭晓东　宋佳玲

摘要：在武器设计研究中，对客体做闪光照相时需要用到脉冲磁场对某一个或几个用于聚焦打靶的电子束团进行调节。为清楚脉冲磁场的强度，分析时变聚焦的效果，基于法拉第电磁感应定律研制用于测量脉冲磁场的脉冲磁场传感器;同时，在分析传统传感器采用固定比例尺寸绕制的特点基础上，根据被测磁场源幅频特性，设计合理尺寸的单匝线圈作为传感器的探头线圈，克服了传统线圈中热噪声电压和由于匝数较多导致的对二次仪表不良影响，并提出解决单匝线圈在测量时“点”性不好的方法。通过实验数据和理论值的对比，验证了方法的有效性。

关键词：脉冲磁场;传感器;灵敏度;修正方法

中图分类号：TM936.7

文献标志码：A

文章编号：1674–5124（2019）03–0114–07

Design and sensitivity correction method of pulsed magnetic field sensor

ZHU Yujie， GUO Xiaodong， SONG Jialing（Metrology and Measurement center， China Academy of Engineering Physics， Mianyang 621900， China）

Abstract： In the weaponry research， when taking flash photography， it is necessary to use a pulsed magnetic field to adjust each of the electron beams for focusing the target. In order to ensure the clarity of the flash photography， a pulse magnetic field sensor for measuring pulsed magnetic field is developed based on Faraday's law of electromagnetic induction. At the same time， on the basis of the analysis of the shortcomings of conventional sensors with fixed proportion size， according to the Amplitude-Frequency characteristic of the measured magnetic field source， a single turn coil with reasonable size is designed as the probe coil of sensor， which overcomes the risk of the thermal noise in the traditional coil and the risk to the second instrument caused by the more turns， meanwhile， a method to solve the problem of “point” in single coil measurement is presented .The validity of the method is proved by comparing experimental data with theoretical values. Keywords： pulsed magnetic field; sensor; sensitivity ; correction method

0 引言

隨着科技的发展，脉冲磁场的应用越来越广泛，脉冲磁场的测量也逐渐发展起来[1-4]。在武器设计研究中，对客体做闪光照相时需要用到脉冲磁场对某一个或几个用于聚焦打靶的电子束团进行调节。因此，脉冲磁场的脉宽和幅值的准确度直接关系到对电子束团的差异性聚焦调节是否可控。然而实际情况是对脉冲磁场的脉宽、幅值等参数的测量仅仅是通过对产生脉冲磁场的励磁电流进行测量并结合产生脉冲磁场线圈尺寸估算得到，而不是对磁场进行直接测量。在此情况下，需要一种能方便应用于在线测量脉冲磁场磁感应强度、脉冲宽度等参数的测量装置。

为了完成对脉冲磁场的测试，国外一些厂家如MOTENA有商用化的用于脉冲磁场测量的探头，但由于探头接地方式复杂，需要整个探头平面接地，不能满足上述原位测量场景;国内一些科研机构也针对科研需要对脉冲磁场测量装置进行了研制，其中一部分利用单匝线圈的绕制方式完成了传感器的研制，如重庆大学针对超高压和特高压变电站内较恶劣的电磁环境研制了纳秒级的脉冲磁场测量装置[1]和军械工程学院对脉冲磁场的测量方法开展了探究[5-6]，然而在对测量线圈进行标定时，标定系统中标准磁场仅存在于亥姆霍兹线圈中心点，所设计的探头面积大于均匀区面积，此时被校探头存在因非“点”性测量而引入的误差;另一部分如上海交通大学为了评估雷电脉冲磁场对敏感信息设备的风险[3]，以及华中科技大学为了完成对脉冲强磁场的测量均采用多匝线圈绕制方式完成了脉冲磁场的测量系统的研制和标定[7]，却没有对多匝线圈产生的热噪声和对二次仪表的影响进行分析;此外，西北核技术研究所研制了积分型脉冲磁场探测器[2]，但没有对探测器的灵敏度进行标定，仅仅对脉宽的响应进行了研究。

综上所述，本文根据脉冲磁场对聚焦打靶的电子束团进行调节的具体场景，基于法拉第电磁感应定律，对现有传感器的优缺点进行了分析，在此基础上开展了脉冲磁场传感器的设计，并针对单匝传感器线圈灵敏度系数的修正方法进行了研究。

1 基本原理

1.1 测量的基本原理

对脉冲磁场测量的方法主要有法拉第电磁感应法、霍尔效应法和磁光效应法3种。霍尔效应法主要用于低频脉冲磁场测量，磁光效应主要用于高频脉冲磁场的测量。在意大利弗拉斯卡蒂召开的国际强磁场会议上，认为对脉冲磁场测量方法主要是法拉第电磁感应法，用磁光效应法作为辅助方法。在此次研究中主要采用法拉第电磁感应法作为测量的主要方法[4-5]。

根据法拉第电磁感应定律，感应电动势与穿过回路所围面积的磁通量的时间变化率成正比，脉冲磁场测量理论公式推导为：

式中：e——感应电动势;

N——线圈匝数;

φ——通过线圈的磁通量;

S——线圈面积;

B——被测磁场的磁感应强度。

如果B（0）=0，积分时间从0到被测时间tm出现峰值，此时脉冲磁场为：

由式（2）可知，为了完成脉冲磁场的测量，可以通过测量感应线圈的感应电动势再对其进行积分来完成。

1.2 脉冲磁场传感器的基本原理

传感器的灵敏度就是传感器输出信号与被测信号的比例[8-9]，若将积分后的信号u看作是传感器的输出信号，可得：

当用单匝线圈绕制成探头线圈时，N=1，在不考虑分布参数的情况下传感器的灵敏度就是线圈的有效面积：

2 感应线圈的设计

2.1 感应线圈匝数选取

脉冲磁场传感器的尺寸选取目前已经有了统一的规定：需要在点性足够好（可忽略其几何尺寸）的同时灵敏度又要足够高，选择圆柱形探头，并且在满足式（5）的前提下可以将通过线圈的磁通看作是均匀的[6]：

式中：R1——圆柱形探头的内径;

R2——圆柱探头的外径;

h——圆柱探头的高。

为满足式（5），探头需要做成具有多匝绕线的圆柱形探头，然而随着匝数的增加，有以下两点不利因素会影响测量结果：

1）由式（1）的推导可知随着探头匝数的增加对应的感应电动势也会增加，在测量高场强的过程中，探头输出的电压势必会对与探头相连的二次仪表产生较大危害。

2）根据最低热噪声电压公式可知，利用相同的传感器探头对脉冲磁场进行测量时，在频率固定的情况下，最低热噪声电压随着线圈匝数的增加而增加。最低热噪声电压公式为：

式中：UN——最低热噪声电压，V;

T——热力学温度，K;

kB——波尔兹曼常数，值为1.38×10–23J/K;

f——频率，MHz;

ρ——电阻率，Ω/m;

D——线圈直径，mm;

d——导线直径，mm。

如在1MHz频率点，在热力学温度为293K时，利用线径为0.001mm的漆包线绕制成直径为1mm的传感器线圈对脉冲磁场进行测量时，由热噪声电压引入的绝对误差可达1.35～135Gs（1Gs=10?4T），具体参数如表1所示。

若加上频率影响因素，如图1所示，在保证传感器探头上限截止频率足够宽的情况下，利用相同匝数的传感器在不同频率下对脉冲磁场进行测量时，频率越大，其最低热噪声电压也越高，这就使得由热噪声电压引入的绝对误差也越大，因此传感器探头对高频下的测量就更加不准。

根据以上分析，为减小对二次仪表的危害和熱噪声电压引入的误差，本文采用单匝线圈绕制的传感器探头来完成对脉冲磁场的测量。

2.2 感应线圈尺寸设计

单匝线圈直径R与其最高可测信号的最大频率fmax之间的关系[9-10]如式（7）所示，其中光速c=3×108m/s，因此对感应线圈的直径选择需要根据具体被测脉冲磁场源的频率来确定。

根据实际情况，如本次实验所用的脉冲磁场源主频为1MHz，那么感应线圈的直径需要小于190.9mm。

2.3 感应线圈形态设计

在对感应探头进行形态设计时，考虑到脉冲磁场产生线圈的具体形态，对感应线圈的设计采用线圈表面垂直于同轴信号传输杆的方式来完成。由于单匝线圈的线圈面积就是传感器的灵敏度，因此感应线圈要求不易形变且面积可准确测量，采用漆包线绕制在具有准确圆度的骨架上完成线圈的绕制，对线圈面积的计算可以通过对骨架截面面积的计算来完成。将探头绕线的一端与同轴线内导体相连，另一端与外导体相连，同轴线末端接SMA头以便通过电缆与示波器连接从而完成信号采集。感应探头实物如图2所示。

3 实验

3.1 实验系统简介

实验系统由可编程电源输出可调电压经过高压直流源提升至千伏级，再给由电容和电感组成的脉冲形成网络（PFN）充电，通过高压脉冲发生器产生触发脉冲触发三电极气体开关，在匹配负载上产生一个高压脉冲大电流，由罗科夫斯基线圈接示波器进行电流监测;同时，输出端经过电缆串联一个单匝线圈，通过该线圈可激发出一个脉冲磁场，该脉冲磁场应与脉冲大电流具有相同的脉宽，其幅度随脉冲大电流幅度的增加而增加。

根据安培环路定理，脉冲磁场的最大值出现在线圈的中心位置，因此将被测传感器探头通过三坐标机准确放置在磁场线圈中心位置，另一端通过同轴电缆接示波器来监测探头所测量到的微分信号，利用Matlab对微分信号进行数字积分从而还原被测磁场值。

3.2 标准脉冲磁场的产生

利用脉冲励磁电流激励对应的磁场线圈可以在线圈内产生脉冲磁场，脉冲磁场场强大小与脉冲磁场激励电流大小成正比[11-12]。线圈常数定义为通过线圈的单位电流所能激励出的磁场值，即k=B/I，知道了磁场线圈的线圈常数，就能通过测量流过的电流完成产生的标准场的计算，同时也反映出脉冲磁场波形和励磁电流波形具有一致性。

根据其尺寸对线圈常数的理论值计算如表2所示，通过该表可以发现，线圈常数随脉冲电流源的频率增加而增加，若要确定线圈常数，需要先确定脉冲磁场源的主频率。由于本次实验所用的脉冲磁场源主频为1MHz，通过表2可知，其线圈常数为0.2330084Gs/A。

3.3 传感器线圈尺寸的确定与测量

根据式（7），选用直径分别为4mm、6mm、10mm3种不同尺寸的骨架来完成磁感应线圈的加工。由于磁感应线圈的面积大小就是传感器的灵敏度，因此对3种尺寸的骨架直径进行多次标定，并取其平均值作为传感器线圈的直径值，3种骨架的标定值如表3所示。

3.4 实验结果

由传感器探头转换后的电信号是一个微分信号，如图3所示，因此需要对该微分信号进行积分从而完成对磁场的测量。本文采用数字积分的方式对微分信号进行积分，具体方式是将图3所示的信号经傅里叶变换后，用带通滤波器对两个集中能量区进行滤波，再对滤波后的时域信号进行积分，得到的积分信号的波形如图4所示，该信号与罗氏线圈所监测的电流信号（图5）具有相同的脉宽。

为了测出脉冲磁场的幅值，需要测量该积分电信号的幅值并通过式（2）进行计算，得出与之对应的磁场值。基于此，对3种不同尺寸的探头测量数据进行记录和计算，表4、表5、表6所记录的分别是直径为4mm、6mm、10mm的传感器线圈所采集的磁场信号。其中脉冲励磁电流由罗氏线圈测得;感应线圈积分电压幅值是传感器所测得的微分信号经数字积分器后所得信号的幅值;磁场强度是由积分信号根据灵敏度系数转换而来，转换方式如式（2）;线圈常数表示每单位电流所能激励出的磁感应强度，是磁場强度与脉冲励磁电流之比。

4 传感器探头的修正因子和灵敏度推算

由磁力线的分布可知，越靠近磁场线圈表面其磁力线分布就越密。若以中心点为圆心，用不同半径的感应线圈测量在该种状态下的磁场强度，其测量结果是不一样的，由式（1）进一步推导可知：

其中，B?（r）表示半径为r的线圈内的平均磁场强度。由式（8）可知，不同半径的磁感应线圈所测出

的磁场强度是通过该感应线圈所围面积的磁通所产生的磁场强度的平均值，因此磁场发生线圈中心点的磁感应强度可以用以中点为圆心、半径趋近于0的磁感应线圈来测量。

同时由于B=k·I，即磁场强度随着脉冲励磁电流的增加而线性增加，对表4、表5、表6中的磁场强度—脉冲磁场电流进行一次项拟合，结果如图6所示。

在图6中，红线表示直径为10mm线圈的磁场响应曲线，黑线表示直径为6mm线圈的磁场响应曲线，蓝线表示直径为4mm线圈的磁场响应曲线，其斜率即线圈常数。由于线圈常数与感应线圈面积相关，用k1（s）、k2（s）、k3（s）分别表示直径为10mm、6mm、4mm线圈所测得的线圈常数，可知k1（s）=0.3243Gs/A，k2（s）=0.3159Gs/A，k3（s）=0.3003Gs/A。

若用k（s）表示磁场发生线圈的实际线圈常数，那么：

其中，D表示感应线圈直径，f（D2）为线圈的场因子，均为D的二次项。

同时：

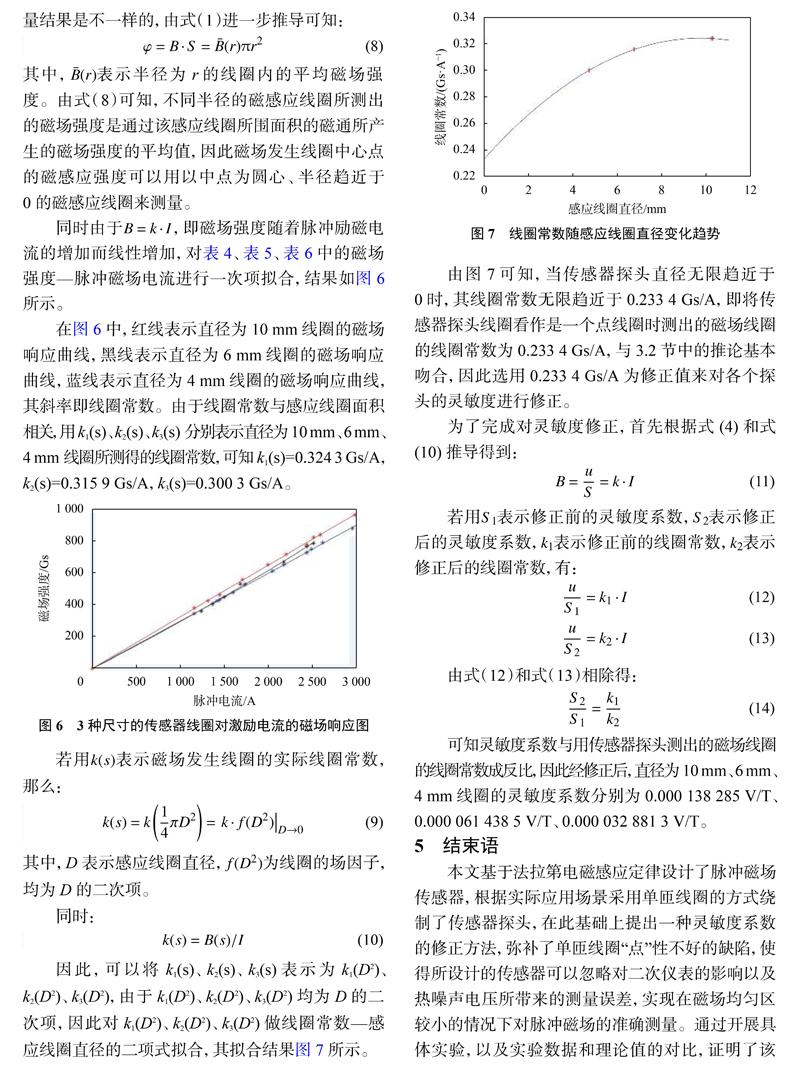
因此，可以将k1（s）、k2（s）、、、k：（s）表示为k（D）、k（D2）、k（D2），由于k（D2）、k（D2）、k（D2）均为D的二次项，因此对k（D2）、k（D2）、k（D2）做线圈常数—感应线圈直径的二项式拟合，其拟合结果图7所示。

由图7可知，当传感器探头直径无限趋近于0时，其线圈常数无限趋近于0.2334Gs/A，即将传感器探头线圈看作是一个点线圈时测出的磁场线圈的线圈常数为0.2334Gs/A，与3.2节中的推论基本吻合，因此选用0.2334Gs/A为修正值来对各个探头的灵敏度进行修正。

为了完成对灵敏度修正，首先根据式（4）和式（10）推导得到：

若用S1表示修正前的灵敏度系数，S2表示修正后的灵敏度系数，k1表示修正前的线圈常数，k2表示修正后的线圈常数，有：

由式（12）和式（13）相除得：

可知灵敏度系数与用传感器探头测出的磁场线圈的线圈常数成反比，因此经修正后，直径为10mm、6mm、4mm线圈的灵敏度系数分别为0.000138285V/T、0.0000614385V/T、0.0000328813V/T。

5 结束语

本文基于法拉第电磁感应定律设计了脉冲磁场传感器，根据实际应用场景采用单匝线圈的方式绕制了传感器探头，在此基础上提出一种灵敏度系数的修正方法，弥补了单匝线圈“点”性不好的缺陷，使得所设计的传感器可以忽略对二次仪表的影响以及热噪声电压所带来的测量误差，实现在磁场均匀区较小的情况下对脉冲磁场的准确测量。通过开展具体实验，以及实验数据和理论值的对比，证明了该方法的有效性，也为进一步研制高准确度的脉冲磁场传感器奠定了基础。

参考文献

[1]粱可道，米彦，李成祥，等.ns级脉冲磁场传感器的研制[J].高电压技术，2009，35（8）：1994-1999.

[2]马良，程引会，吴伟，等.积分型脉冲磁场探测器[C]//中国核学会2009年学术年会会议论文集，2009.

[3]任晓明，傅正财，黄晓红，等.脉冲磁场测量系统的研制与标定[J].上海交通大学学报，2010，44（7）：980-983.

[4]化中工学院强磁场测量科研组.感应法脉冲强磁场测量仪[J].科研报道，1976（1）：49-60.

[5]王锋，刘美金，范江玮.脉冲磁场测试方法及影响因素研究[J].电子测试，2014（1）：124-125.

[6]王锋，米东，徐璋逐.基于法拉第电磁感应法的脉冲强磁场测量方法[J].高电压技术，2008，33（4）：674-677.

[7]丁炜，彭涛，辜承林.脉冲强磁场探测系统的基本实现[J].核电子学与探测技术，2006，26（6）：998-1000.

[8]刘俊，徐雁.脉冲强磁场测量系统的设计与仿真分析[J].电测与仪表，2006，43（9）：11-14.

[9]毛振珑.磁场测量[M].北京：原子能出版社，1985：127-135.

[10]MOTOHISA KANDA.Standard probes for electromagnetic field measurements[J].IEEE Trans on Antennas as and Propagation，1993，41：1349-1364.

[11]张卫东，崔翔.光纤瞬态磁场传感器的研究及其应用[J].中国电机工程学报，2003，23（1）：88-92.

[12]王珏，张适昌，严萍，等.用自积分式罗氏线圈测量纳秒级高压脉冲电流[J].强激光与离子束，2004，16（3）：399-403.

（编辑：李刚）