民用飞机气动伺服弹性试飞激励响应仿真研究

雷鸣 杨飞 霍幸莉

摘要：为提高民用飞机气动伺服弹性试飞仿真预测能力，实现高效安全的民用飞机气动伺服弹性试飞。在民用飞机气动伺服弹性试飞方法的基础上，提出民用飞机气动伺服弹性试飞激励响应仿真方法。该方法以民用飞机全机动力学有限元模型为基础，建立带飞行控制律的飞机气动伺服弹性模型，通过副翼、升降舵和方向舵的激励分别实现对飞机的激励响应仿真，得到飞机结构响应量值。为进一步验证该方法的可行性，进行某民用飞机副翼脉冲激励响应仿真，并将仿真响应结果与试飞结果对比，响应幅值相差15.3%，满足工程要求。民用飞机气动伺服弹性试飞仿真很好地预测试飞激励的飞机响应，为试飞激励信号的优化以及结构响应的评估提供技术参考。

关键词：民用飞机;气动伺服弹性;飞行试验;激励响应;仿真

中图分类号：V211;V217 文献标志码：A 文章编号：1674-5124（2019）06-0146-07

收稿日期：2018-07-07;收到修改稿日期：2018-08-12

作者简介：雷鸣（1987-），男，陕西西安市人，工程师，硕士，主要从事飞行结构动力学研究。

0 引言

飞机气动伺服弹性（aeroservoelastic，ASE）是非定常气动力、飞行控制系统以及飞机结构动力（弹性力、惯性力）之间的耦合，会产生ASE不稳定现象[1]。现代飞机尤其是先进民用飞机、运输机和高性能战斗机，普遍采用了电传飞行控制系统[2]。随着现代飞机柔性的增大，飞机结构与飞行控制系统之间的耦合变得不可忽略，而且这种耦合对飞行稳定性的影响往往是不利的，因此刚体飞机已经不能满足飞行稳定性的要求。

美国的YF-16、YF-17、F-18、X-29飞机在早期飞行试验中就曾经遇到过这种气动伺服弹性不稳定现象。以YF-16为例[3]，理论分析表明其不存在不稳定现象，但是在飞行试验中出现了强烈振动;经对飞机的响应数据分析，确定这是一种气动伺服弹性不稳定现象，是由于翼尖导弹俯仰模态与控制系统横滚回路耦合所引起的一种不稳定问题。现代民用飞机普遍采用电传飞行控制系统，采用主动控制设计理念，加之对飞机质量的要求，飞机机翼柔性更大，更易发生ASE现象。对飞机进行气动伺服弹性稳定性分析及试验已经成为现代飞机开发研制过程中必不可少的环节。

飞机在设计阶段通过模型，根据经典的自动控制系统理论在频域内分析飞机气动伺服弹性的稳定性;而后通过飞机结构与飞控系统的地面耦合试验进一步分析气动伺服弹性稳定性，最后进行飞机气动伺服弹性飞行试验。

飞行试验过程中，需要对飞机施加一定的外激励扰动，从而获得飞机ASE系统的输入输出。激励的量值如何选取，飞机的响应结果如何，这都是飞行试验设计者所关心的。如果激励量值偏小，则飞机响应小，响应数据信噪比低;量值偏大会对飞行试验带来风险。因此，迫切需要对飞机ASE试飞激励进行仿真预测，为飞行试验激励方式、激励量值的选取提供仿真方法，保证飞行试验效率与安全。

国内外开展了大量的ASE试飞研究，如YF-17飞机的系统和飞机结构动力学耦合的增益响应研究[4]，YF-16飞机的控制系统和结构交互动力学特性研究[5]，狂风战机的滚转通道和俯仰通道的ASE稳定性研究[6]，F/A-18飞机带推力矢量的ASE分析模型研究[7]以及基于F/A-18C的飞行试验进行了ASE预测[8]研究等。

本文建立一种民用飞机ASE试飞激励响应仿真方法，该方法在民用飞机结构动力学模型、控制律模型以及非定常气动力模型的基础上，进一步建立操纵面激励响应仿真模型，实现了民用飞机ASE试飞激励响应仿真，为飞行试验设计提供激励响应仿真预测技术。

1 气动伺服弹性飞行试验概述

飞机ASE试飞是飞机ASE设计的最终环节，也是验证飞机ASE特性的最重要环节。民机ASE试飞属于适航条款25.629要求。25.629条款并没有对ASE试飞提出包线要求与裕度定量指标要求。民机ASE试飞稳定性要求参照军机ASE稳定性要求。

ASE试飞时飞控系统为闭环状态，用闭环的方法测试回路总的开环传递函数的频响特性，给出试飞状态点的氣动伺服弹性稳定裕度。试飞时激励输入信号类型包括正弦扫频信号和脉冲信号。在每个试验点上，飞机受到试验所需的副翼、升降舵和方向舵激励及其他激励，飞机产生一定的响应输出信号，通过输入和输出信号辨识飞机的开环传递函数，分析飞机ASE稳定性。ASE试飞时采用从高高度到低高度，从小表速到大表速逐渐接近飞行包线边界的方法进行，选择的速度增量应保证速压的增量接近于恒值，每次应根据对前几个试验点的数据处理结果确定速度或速压增加情况。

ASE试飞中，激励信号频率范围与激励信号幅值大小，一方面根据飞机本身结构及飞控系统特点选取;另一方面为保证试飞安全，根据以往试飞经验，激励信号都是从小到大依次选取，直到能够激起ASE系统的响应，获得较好的信噪比数据。

副翼反对称激励用于测试滚转回路ASE裕度;升降舵对称激励测试俯仰回路ASE裕度;方向舵激励测试偏航回路ASE裕度。在每次激励后留有足够时间使飞机的响应完全衰减后再进行下次激励。

2 民机气动伺服弹性试飞建模

2.1 结构动力学建模

ASE试飞动力学建模技术主要包括结构动力学建模技术、气动力建模技术和飞控系统建模技术。飞机结构动力学模型包括结构刚度、质量和阻尼，模态包括刚体模态和弹性模态。

结构刚度包括刚度及其刚度分布。全机机身、机翼、垂尾和平尾要按各个站位的刚度等效模拟，机身与机翼、机翼与平尾、机身与垂尾、机翼与发动机的连接刚度用柔度矩阵模拟。结构刚度和刚心根据薄壁结构闭室原理或力法计算确定。利用力（力矩）与变形的关系，得到相应的刚度计算关系式。

结构质量涉及质心、质量和惯量，包括结构质量、系统质量、燃油质量及其分布、商载质量及其分布，还包括操纵面质心、质量和绕轴转动惯量。重心，重心转动惯量是指绕零件自身重心的极惯性矩和惯性积。

结构阻尼影响结构的响应特性。响应分析中弹性模态阻尼系数一般取0.03，保守取0.02。颤振分析模型通常不考虑阻尼;如果需要考虑阻尼，可以采用全机地面共振试验的阻尼结果。

利用地面共振试验结果对基准状态的结构理论模型进行修正，修正后主要模态分析结果与试验结果相比，频率偏差应在5%以内，模态指示函数满足期望要求。

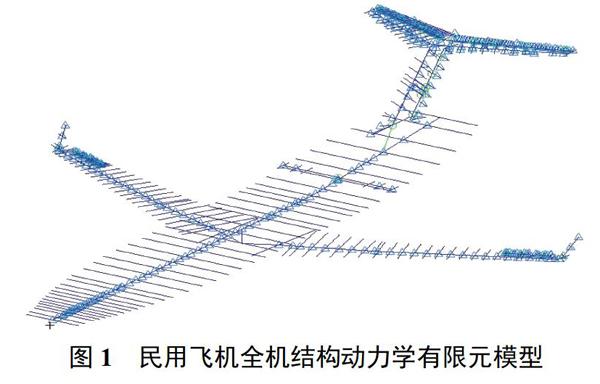
民用飞机全机结构动力学有限元模型如图1所示。

2.2 气动力建模技术

气动弹性稳定性分析中的气动力模型，对不可压缩或可压缩气流的非定常气动力，三元面元法可以获得更好的升力面间交互的气动力模型，使用气动力偶极子格网法进行计算。通常应该考虑主要翼面（机翼、平尾、垂尾）、操纵面（副翼、升降舵、方向舵、襟翼、缝翼）以及机身的气动力;对翼吊发动机必须考虑发动机气动力和吊挂气动力;对T型尾翼类升力面交互作用，应考虑如T尾效应类的升力面交互影响。

定义X轴为机身轴方向（顺气流方向），Y轴为垂直机身轴方向（侧向），z轴为垂直机翼平面方向（垂向），对每个片条6个自由度上的气动力加以分析，对应的气动力可表示为

F=[L_xL_yL_zM_xM_yM_z]^T（1）

用物理位移矩阵形式，F表示为

F=Aw，w=[δx δy δz φ α β]^T（2）式中：w——采用刚性片条假设，忽略其弦向变形的运动自由度;

δ_x——气流方向位移分量;

δ_y——侧向位移分量;

δ_z——垂向位移分量;

φ——绕x轴的滚转角;

α——绕y轴的俯仰角;

β——绕z轴的偏航角;

A——非定常气动力影响系数矩阵。

片条的物理坐标与模态坐标的关系为

w=Φq（3）式中：w——物理位移坐标;

q——模态坐标;

Φ=[φ₁，φ₂，φ₃，φ₄，φ₅，…，φ_n]——片条气动力参考点对应的n阶正则固有模态;

φ_i——第i阶正则模态对应的6个物理坐标的特征向量值[T₁T₂T₃R₁R₂R₃]。

非定常气动力矩阵为式中：m——平尾片条总数;

φ_j6×n——第j个片条对应的n阶模态列阵;

A_j6×6——第j个片条对应的气动力影响系数矩阵。

2.3 飞控系统建模技术

控制系统模型包括任何控制系统的传感器单元和结构模态之间的交互仿真，控制律传递函数与结构耦合。包括俯仰、滚转、偏航主回路控制系统模型，包括陷幅滤波器控制环节。将飞控系统的传感器布置在结构振动小的地方，机翼垂直一弯模态节线位置;在敏感频率加陷幅律波器控制回路总增益。

操纵面作动器、惯导设备（IRS等）和控制律都会对气动伺服弹性造成影响，但影响ASE问题和解决ASE问题的关键是结构陷幅滤波器。

在反馈控制回路中增加结构陷幅滤波器。其传递函数可表示为式中，ω₁，ω₂为陷幅中心频率。

3 民用飞机气动伺服弹性试飞激励响应仿真

3.1 激励响应仿真建模

飞机气动弹性响应分析，模态坐标系气动弹性频率响应分析方程表示为式中：M_hh——模態质量阵;

B_hh——模态阻尼阵;

K_hh——模态刚度阵;

Q_hh——气动力矩阵，为马赫数Ma和减缩频率

k=ωc/2V的函数;

ω=2πf——圆频率;

f——频率;

c——参考弦长;

V——气流速度;

ρ——气流密度;

g=2γ——人工阻尼;

γ——衰减率;

u_h——模态向量;

P（ω）——模态坐标下的载荷，包括气动力载荷PHF₂（ω）和非气动力载荷PHF（ω）动两个部分，即：{P（ω）}={PH₂F（ω）}+{PHF（ω）}。

将飞控系统模型加入式（6）可得ASE模型方程[9]如下式所示：式（7）是求解线性控制系统的基本方法。式中，ζ（s）是模态坐标矢量;M_ζδ为操纵面和飞机主模态耦合惯性力;M_δδ为操纵面广义质量矩阵;Q_ms为固有模态引起的广义非定常气动力系数;Q_CS是控制系统操纵面运动引起的广义非定常气动力系数;k为减缩频率;6（s）控制系统变形，包括操纵面变形，见下式：

{δ（s）}=[T（s）]{Y（s）}（8）式中[T（s）]是控制系统和作动器传递函数矩阵，{Y（s）}为传感器输入变形和偏度信号，见下式：

{Y（s）}=[Φ_y]{ζ（s）}（9）式中[Φ_y]是飞机机身陀螺仪位置传感器位置模态变形。

激励响应仿真分析模拟了飞机各个结构部件的惯性力、弹性力、气动力、控制律。根据各个试验点激励响应模拟仿真模型进行计算，能够输出任意有限元节点振动加速度或位移数据。

3.2 激励响应仿真分析方法

激励响应分析方法分为模态频率响应法和直接频率响应法，其中模态频率响应法适用于较大模型以激振频率范围广的激励响应仿真，因此选用模态频率响应法。基本方法如下：

利用模态坐标变换公式（10），将物理坐标下结构振动方程转换成模态坐标下的振动方程，利用固有模态振型的正交性，对方程进行解耦，得到模态坐标系下结构的振动方程：

将公式（11）写成单自由度形式为

用模态法求得：

模态位移响应公式为

由式（14）求得η_i和η_i，代入式（13）即可由模态加速度法求出系统的响应。将上述方法应用于ASE仿真模型方程式（7）即可进行激励响应仿真。

3.3 激励响应仿真

3.3.1 单机翼激励响应仿真

图2所示15°后掠单机翼颤振模型，是颤振分析标准模型[10]。该机翼颤振速度为147.2m/s，通过在机翼翼尖后缘施加脉冲激励输入，输出机翼翼尖中垂向位移响应，研究不同速度下其响应特性，在0.4s时间内施加2个脉冲激励。分析表明：当速度为127.0m/s时响应位移较小，迅速衰减，飞机稳定;146.0m/s响应位移变大，衰减缓慢，但飞机稳定，如图3所示。当速度等于颤振速度时，响应位移为等幅振荡，飞机临界稳定，如图4所示。当速度大于颤振速度，为148.6m/s时响应位移放大，迅速发散，飞机不稳定，如图5所示。

3.3.2 全机ASE激励响应仿真

下面以带飞行控制律的民机全机激励响应仿真模型进行ASE激励响应仿真计算。对飞机滚转通道进行副翼反对称扫频激励和脉冲激励。某飞行状态，扫频激励副翼偏度为0.2°，扫频范围0.1～100Hz。脉冲激励副翼偏度为3.0°。副翼脉冲激励舵面偏度时间历程如图6所示。

副翼扫频激励，机翼、副翼响应的振动加速度见图7;副翼脉冲激励，机翼、副翼响应的振动加速度见图8。

4 激励响应仿真与试飞结果对比

以某民用飞机飞行试验副翼反对称脉冲激励结果进行验证。某飞行状态，副翼偏度20脉冲激励，研究机翼翼尖的气弹响应特性。副翼脉冲激励副翼偏度时间历程如图9所示。试飞副翼脉冲结果如图10所示，激励响应仿真结果如图11所示。对比试飞数据和分析数据，试飞结果第1个峰加速度响应值为1.39，激励响应仿真结果第1个峰加速响应值为1.59，激励响应幅值相差15.3%，满足工程需要。

5 结束语

本文结合民用飞机气动伺服弹性试飞需求，研究了民用飞机气动伺服弹性试飞仿真预测技术。将副翼脉冲激励试飞激励响应结果与仿真预测激励结果进行对比，对比了机翼翼尖的结构振动响应，仿真结果比试飞结果结构振动幅值大15.3%，满足工程应用要求，证明了本文研究的工程应用价值。本方法能够预测气动伺服弹性试飞中的结构振动响应，使试飞工程师在开展试飞前，能够掌握飞机在激励时的振动响应水平，更好地开展安全监控，保障试飞安全。未来可利用该技术实现对试飞中激励信号选取进行优化以及振动传感器布置位置的优化。

参考文献

[1]杨超，黄超，昊志刚，等.气动伺服弹性研究的进展与挑战[J].航空学报，2015，36（4）：1011-1033.

[2]吴森堂，费玉华.飞行控制系统[M].北京：北京航空航天大学出版社，2009：139-144.

[3]LAWRENCE J，HUTTSELL R D，KROBUSEK，HOWARI）L，FARMER.Application of three aeroservoelastic stabilityanalysis techniques[R].AFFDL，1976.

[4]ARTHURS T D，GALLAGHER J T.Interaction betweencontrol augmentation system and airframe dynamic on the YF-17[C]//16th Structural Dynamics，and Materials Conference.AIAA，1975.

[5]PELOUBET R P.YF-16 active control system/structuraldynamic interaction instability[C]//16th Structural Dynamics，and Materials Conference.AIAA，1975.

[6]LOTZE A，SENSBURG O，KUHN M.Flutter investigation ofa Combat aircraft with a command and stability augmentationsystem[J].Journal ofAircraft，1976，14（4）：368-374.

[7]BRENNER M J.Aeroservoelastic modeling and validation ofthrust vectoring f/a-18 aircraft[R].NASA，1996.

[8]THOMPSON P M，KLYDE D H，FARHAT C，et al.Aeroservoelastic predictive analysis capability[C]//AIAAAtmospheric Flight Mechanics Conference and Exhibit.AIAA，2007.

[9]MUKHOPADHYAY V.Flutter suppression control lawdesign and testing for the active flexible wing[J].Journal ofAircraft，1995，32（1）：45-51.

[10]RODDEN W P，HARDERARDE.Aeroelastic addition toNASTRAN[R].NASA，3094.

（編辑：莫婕）