基于超像素的流形正则化稀疏约束NMF混合像元分解算法

李登刚 陈香香 李华丽 王忠美

摘 要：針对传统非负矩阵分解（NMF）法用于高光谱图像混合像元分解时产生的分解结果精度不高、对噪声敏感等问题，提出一种基于超像素的流形正则化稀疏约束NMF混合像元分解算法——MRS-NMF。首先，通过基于熵率的超像素分割来构造高光谱图像的流形结构，把原图像分割为k个超像素块并把每个超像素块中具有相似性质的数据点标上相同的标签，定义像素块内有相同标签的任意两个数据点之间的权重矩阵，然后将权重矩阵应用于NMF的目标函数中以构造出流形正则化约束项;第二，在目标函数中添加二次抛物线函数以完成稀疏约束;最后，采用乘法迭代更新法则求解目标函数以得到端元矩阵和丰度矩阵的求解公式，同时设置最大迭代次数和容忍误差阈值，迭代运算得到最终结果。该方法有效利用了高光谱图像的光谱和空间信息。实验结果表明，在模拟的高光谱数据中，与传统的流形稀疏约束的非负矩阵分解（GLNMF）、L1/2-NMF和顶点成分分析全约束最小二乘法（VCA-FCLS）等方法相比，MRS-NMF可以提高0.016～0.063的端元分解精度和0.01～0.05的丰度分解精度;而在真实的高光谱图像中，MRS-NMF较传统的GLNMF、顶点成分分析法（VCA）、最小体积约束的非负矩阵分解（MVCNMF）等方法可以平均提高0.001～0.0437的端元分解精度。所提MRS-NMF算法有效地提高了混合像元分解的精度，同时具有较好的抗噪性能。

关键词： 混合像元分解;非负矩阵分解;超像素分割;流形正则化;稀疏性

中图分类号：TP751.1

文献标志码：A

Abstract：For the problems such as poor unmixing results and sensitivity to noise of traditional Nonnegative Matrix Factorization （NMF） applied to hyperspectral unmixing， a Manifold Regularized Sparse NMF with superpixel （MRS-NMF） algorithm for hyperspectral unmixing was proposed. Firstly， the manifold structure of hyperspectral image was constructed by superpixel segmentation based on entropy. The original image was divided into k-superpixel blocks， and the data points in each superpixel block with same property were labeled the same label. Weight matrices were defined between any two data points with the similar label in a superpixel block， and then the weight matrices were applied to the objective function of NMF to construct the manifold regularization constraint. Secondly， a quadratic parabola function was added to the objective function to complete the sparse constraint. Finally， the multiplicative iterative update rule was used to solve the objective function to obtain the solution formulas of endmember matrix and abundance matrix. At the same time， maximum iteration times and tolerate error threshold were set to get the final results by iterative operation. The proposed method makes full use of spectral and spatial information of hyperspectral images. Experimental results show that on synthetic data the unmixing accuracies of endmember and abundance based on proposed MRS-NMF are 0.016-0.063 and 0.01-0.05 respectively higher than those based on traditional methods like Graph-regularized L1/2-Nonnegative Matrix Factorization （GLNMF）， L1/2NMF and Vertex Component Analysis-Fully Constrained Least Squares （VCA-FCLS）; while on real hyperspectral images， the average unmixing accurary of endmember based on proposed MRS-NMF is 0.001-0.0437 higher than that of traditional GLNMF， Vertex Component Analysis （VCA） and Minimum Volume Constrained Nonnegative Matrix Factorization （MVCNMF）. This proposed algorithm improves the accuracy of unmixing effectively with good robustness to noise.Key words： hyperspectral unmixing;Nonnegative Matrix Factorization （NMF）; superpixel segmentation; manifold regularization; sparseness

0 引言

随着卫星和高光谱成像技术的发展，高光谱图像拥有较高的光谱分辨率以及丰富的光谱波段。然而由于空间分辨率的限制，高光谱图像中常常会出现一个像素包含多种地物。地物是指地面上各种有形物（如山川、河流、森林等）和无形物（如省、县界等）的总称，从而形成了混合像元。混合像元的存在，使得传统基于像素级的高光谱图像分类等图像处理方法失去作用。为了解决这一问题，高光谱图像混合像元分解技术随之而生，混合像元分解是将混合的像元分解为各类物质的组成部分（端元）及其相应的组成比例（丰度）。作为一种新的有效的高光谱数据表述方式，混合像元分解技术近年来得到了广泛的关注[1-2]，目前已在农业调查、矿物挖掘、环境监测、军事监督等领域得到了广泛的应用。

近年来，学者们提出了多种混合像元分解方法，总的来讲，这些算法可以分成两类：基于几何学的方法和基于统计学的方法。基于几何学的方法将混合像元构成的空间看成为一个单形体，而各端元则位于单形体的顶点，这类方法需要图像中存在纯像元，常见的方法有：顶点成分分析法（Vertex Component Analysis， VCA）[3]、纯像素指数法（Pure Pixel Index， PPI）[4]、N-FINDR[5]、自动形态学端元提取法（Automated Morphological Endmember Extraction， AMEE）[6]。得到端元后，通常通过全约束的最小二乘法（Fully Constrained Least Squares， FCLS）[7]来求解丰度。基于统计学的方法则将混合像元分解看成盲信号分离问题，因为不需要原图像中存在纯净像元，并且可以同时得到端元和豐度，故该方法非常适用于端元高度混合的复杂场景中。常见的基于统计学的方法是独立成分分析法（Independent Component Analysis， ICA）[8]和非负矩阵分解法（Nonnegative Matrix Factorization， NMF）[9-14]。

NMF作为一种基于统计学的方法，不需要原图像存在纯像元，并且能够同时得到端元和丰度，目前广泛应用于混合像元分解领域。然而由于目标函数的非凸性，在求解过程中，NMF不能求得全局最优解。因此，根据高光谱图像端元和丰度的相关属性，在NMF的目标函数中加入了不同的约束项。

如利用端元几何特性作为目标函数约束项的方法：

最小体积约束的非负矩阵分解（Minimum Volume Constrained Nonnegative Matrix Factorization， MVCNMF）[9]、端元相异性约束的非负矩阵分解（Endmember Dissimilarity Constrained Non-negative Matrix Factorization， EDCNMF）[10]等。以及利用高光谱图像丰度分布稀疏性作为约束项的方法，如L1/2稀疏约束的非负矩阵分解（L1/2 Sparsity-Constrained Nonnegative Matrix Factorization， L1/2NMF）[11]、稀疏性和平滑性约束的非负矩阵分解（Sparse and Smooth Nonnegative Matrix Factorization， SSNMF）等[12]。稀疏性是指在实际的高光谱图像中，各类端元的分布往往会集中在局部区域，而不会充满整个图像空间[3]，是高光谱图像的一种本质属性。还有利用流形正则化作为约束项的方法，如流形稀疏约束的非负矩阵分解（Graph-regularized L1/2-NMF， GLNMF）[13]、图正则化稀疏约束的非负矩阵分解（Graph-regularized NMF， GNMF）[14]等。

研究[15]发现，不能通过图像数据来填充满高维欧氏空间，因此这些数据间存在一个潜在的流形结构。如果原数据空间中的两个数据点很相近，那么在新的空间中，它们仍然会保持相似，这就是流形假设[16]。而对于高光谱图像，如果两个像元在空间结构中相近，那么在丰度图像中，它们也将保持这种相近的关系。

传统的非负矩阵分解方法仅考虑了丰度的稀疏性或者流形结构信息，导致分解精度不高、对噪声敏感等问题。为此，本文充分利用了高光谱图像的相关特性，将流形正则化约束和稀疏约束同时加入到了NMF模型中，提出了基于超像素的流形正则化稀疏约束NMF混合像元分解算法——MRS-NMF（Manifold Regularized Sparse NMF）。

与传统算法相比，该算法既有效地利用了光谱信息，同时又充分挖掘了空间信息。此外，使用超像素分割来建立流形正则项，可以很好地描述像元之间的相似性。合成的模拟数据实验和真实的高光谱图像数据实验结果表明，与其他传统算法相比，该算法可以获得更高的分解精度和更好的抗噪性能。

1 相关理论背景

1.1 线性混合模型

1.2 非负矩阵分解（NMF）

非负矩阵分解是由Lee等[17]提出，其核心思想是把一个非负矩阵分解为另外两个非负矩阵的乘积，给定一个非负矩阵X∈Rn×m，NMF旨在寻找另外两个非负矩阵A∈Rn×r和S∈Rr×m（rmin（m，n）），使得：

正如式（1）与式（4）所示，如果忽略噪声和误差，并且在NMF模型中加入丰度和为1约束：1TPS=1，那么NMF非常适合应用于混合像元分解问题。通过计算X与AS的欧氏距离，从而得到NMF的目标函数如下：

通过乘法迭代更新法则求解式（5），可以得到端元矩阵和丰度矩阵的解。但是在式（5）中，端元A和丰度S的解非唯一，对于任意一个可逆的矩阵D，如果A和S为目标函数的解，那么AD、D-1S也将是目标函数的解。因此，为了获得全局最优解，需要根据实际的物理意义在目标函数中加入约束项以使端元和丰度的解唯一。

2 本文算法

本文提出的MRS-NMF算法旨在提高高光谱图像混合像元分解精度及抗噪性。为了完成这一目标，流形正则化约束和丰度稀疏性约束被添加到了目标函数中。通过超像素分割来表示高光谱图像的流形结构信息，同时通过二次抛物曲线来模拟丰度图像的稀疏性。最后通过最优化算法来求解目标函数，从而得到最终结果。MRS-NMF算法的模型定义如下：

2.1 构造流形正则化约束

为了充分利用高光谱图像的光谱和空间结构信息，本文算法通过基于熵率的超像素分割（Entropy Rate Superpixel， ERS）[18]来构造流形结构。首先把原图像分割为k个超像素块，那么每个超像素块中的各个数据点将具有相似的性质，给它们标上相同的标签。对于具有相同标签的像素块内任意两个数据点xi和xj，定义它们之间的权重矩阵为权重矩阵应设为0。而当两个数据点之间的空间距离越近时，它们之间的权值越大，空间距离越远时，权值越小。通过上述分析，将权重矩阵应用于NMF的目标函数中，构造出流形正则化约束项如下：

其中：N表示像元的数量。由式（7）可知，当两个数据点xi和xj之间的距离越小时，Wij相对较大，使约束项f1（S）最小，从而丰度si和sj越相似。

2.2 构造丰度稀疏约束

正如Qian等[11]所述，使用L1/2范数作为丰度的稀疏约束项，存在着对噪声鲁棒性能差等问题。

本文采用了文献[5]和文献[19]中使用的方法，通过向目标函数添加二次抛物线函数来完成稀疏约束。二次抛物线定义为：

其中：P为端元个数;ξ用来控制稀疏度。通过式（8）对整个丰度图像进行累加操作，从而得到了稀疏约束项如下：

根据上述分析，本文MRS-NMF算法的目标函数如下：

2.3 目标函数求解

得到了目标函数后，最后的问题为目标函数的求解，这里采用乘法迭代更新法则来求解式（10）所示的目标函数。得到端元矩阵和丰度矩阵的求解公式如下：从式（12）可以看出，端元和丰度矩阵的计算方法中只存在加法和乘法运算，从而保证了结果的非负性约束（ANC）。此外，为了使丰度满足和为1约束（ASC），在端元和丰度矩阵每次迭代更新前按照式（13）进行扩展。

其中：δ为控制和为1约束（ASC）的权重参数，本文参考文献[9，11]将δ设为15，1TP和1TN分别为P个元素和N个元素全为1的行向量。在每次迭代计算前，先通过代替A，代替X，计算完成后再从和中取出A和X。再进行式（13）所示的扩展，进行下一次迭代计算，达到迭代停止条件时，停止迭代求出结果。

接下来的问题是迭代停止条件，采用设置最大迭代次数和容忍误差。本文参考文献[9-12]，将最大迭代次数设置为3000，容忍误差设置为10-6。即当连续10次的迭代误差都小于10-6或者计算达到最大迭代次数时，停止迭代得到最终结果。

本文MRS-NMF算法步骤如下。

算法1 MRS-NMF算法。

输入 高光谱图像X，端元个数P。

输出 端元矩阵A和丰度矩阵S。

步骤1 设置参数λ、 μ和K。

步骤2 使用ERS超像素分割构造权重矩阵W。

步骤3 初始化端元矩阵A和丰度矩阵S，对丰度矩阵S的列作归一化处理。

步骤4 按照式（11）迭代计算矩阵A。

步骤5 按照式（13）扩展矩阵A和X分别为和。

步骤6 按照式（12）迭代计算矩阵S。

步骤7 返回步骤4继续计算，直到满足迭代停止条件时为止。

步骤8 达到迭代停止条件时，停止迭代，得到最终结果。

3 实验与结果分析

3.1 评价指标

本章通过合成的模拟数据实验和真实的高光谱图像数据实验来验证本文MRS-NMF算法的有效性。本文采用两个评价指标来衡量算法的性能，分别是用来评价端元的光谱角距离（Spectral Angle Distance， SAD）和用来评价丰度的均方根误差（Root Mean Squared Error， RMSE）。SAD和RMSE的定义如下：

其中：a为参考的端元向量;为估计的端元向量;s为参考的丰度向量;为估计的丰度向量;N为丰度图像像素的数量。从定义式可以看出，SAD和RMSE越小，估计值和真实值越相近，分解的结果精确度越高。

3.2 实验条件

本文所有的数据计算均在硬件环境为Intel Core i3-2330，内存4GB，主频2.2GHz，软件环境为Matlab R2014b的计算机上进行。

3.3 模拟数据实验

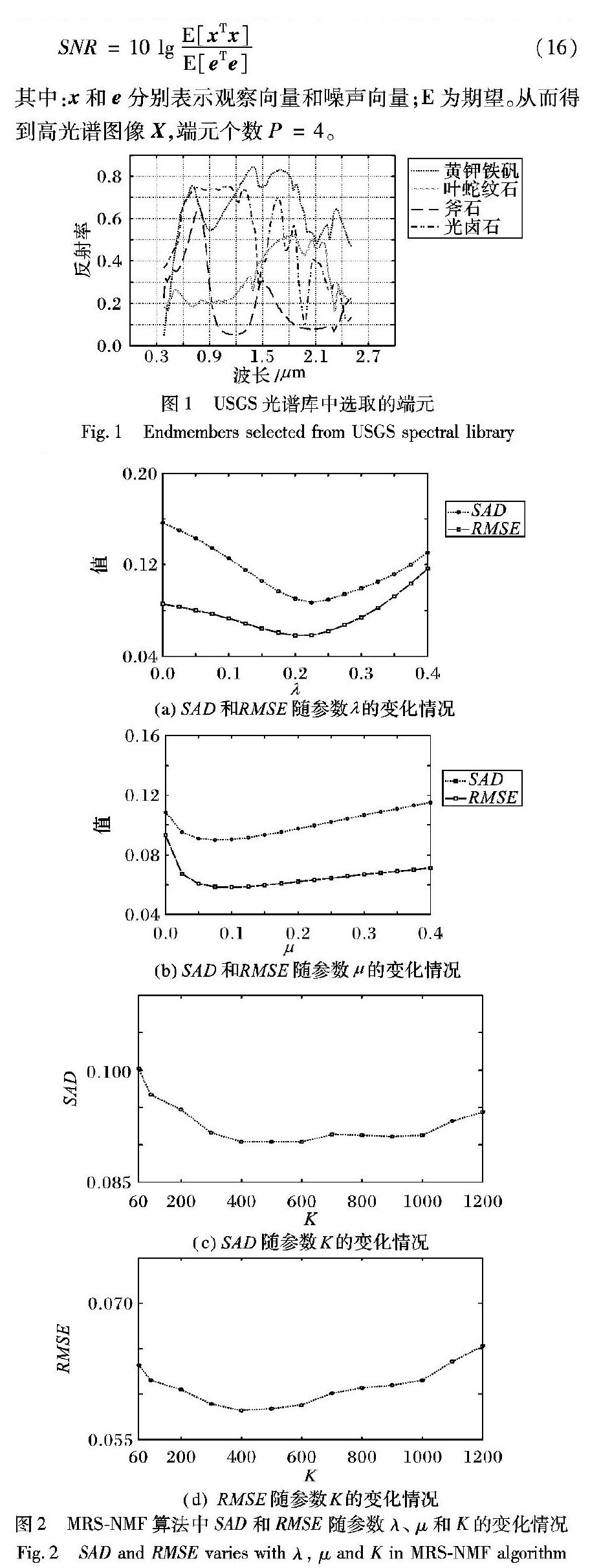
为了测试本文算法的性能以及确定算法中各个参数的最优值，从美国地质勘测局（United States Geological Survey， USGS）的光谱库中选取了4种矿物光谱曲线来合成模拟图像数据。这些光谱包含了224个光谱波段，波长范围在0.38～2.5μm。图1为这4种物质的光谱曲线，它们分别是黄钾铁矾、叶蛇纹石、斧石和光卤石。参考MVCNMF[9]中的方法，通过下述步骤来合成模拟图像：1）将尺寸大小为64×64的图像平分为8×8的小块;2）从光谱库中随机选取任意一种纯像元来填充上述各个小块，这样每个小块的像素均为纯像元;3）使用一个7×7的低通滤波器来产生混合像元，这样可以得到每個像元的丰度比例;4）为了更进一步去除图像中的纯像元，并且控制丰度的稀疏程度，对于丰度大于0.8的像素，将会被上述4种端元均匀填充，这样各种端元的丰度均为1/4。为了更进一步贴近真实的高光谱图像，充分考虑可能出现的误差和噪声，通过向图像添加不同信噪比（Signal-to-Noise Ratio， SNR）的零均值高斯白噪声来实现。SNR定义为：

在本实验中，需要确定三个参数值：流形正则化约束参数μ、稀疏约束参数λ和超像素的个数K。其中：参数λ用来控制丰度的稀疏度，参数μ用来控制结构信息所占的权重，而参数K则由图像本身特点决定。将模拟数据中的信噪比SNR设为20dB，端元矩阵A和丰度矩阵S选择随机初始化，并在每次实验中保持不变。

参考文献[12-13]中的参数设置，首先通过固定参数μ=0.1，K=400来确定参数λ的最优值，将λ以0.025的步长从0增加到0.4。按照算法1中的步骤，首先求解出端元矩阵和丰度矩阵，然后根据式（14）和（15）分别计算出不λ同下SAD和RMSE的值。图2（a）表示所提出MRS-NMF在不同λ值下SAD和RMSE的变化情况。从图2可看出：在0～0.2的区间范围内，SAD和RMSE都随着λ的增加而减小;而在λ大于0.2后，SAD和RMSE则随着λ的增加而增加。所以，这里选择λ的最优值为0.2。

然后固定λ=0.2，K=400，改变μ以0.025的步长从0增加到0.4。同样按照算法1中的步骤，先求解出端元矩阵和丰度矩阵，根据式（14）和（15）计算出不同μ下，SAD和RMSE的值。不同μ值下，所提出方法求得的SAD和RMSE如图2（b）所示。由图2（b）可知：当μ位于0～0.1的区间范围内时，SAD和RMSE都随着μ的增加而减小;当μ大于0.1后，SAD随着的μ增加而增加，而RMSE则保持相对平稳。所以综合考虑SAD和RMSE的变化情况，这里选择μ的最优值为0.1。

最后固定λ和μ的值分别为0.2和0.1，改变K的值在60～2000内变化。采用同样的方法，求解出不同K值下SAD和RMSE的值。图2（c）、（d）为在不同K值下，SAD和RMSE的变化情况。从中可看出：随着K的增加，SAD和RMSE均呈现出一个先降后升的过程，且SAD和RMSE都在K=400时取得最优值，由于K与图形本身特征有关，所以在此选择K的最优值为400。

通过上述实验，从而确定了算法中各个参数的最优值分别为：λ=0.2， μ=0.1，K=400。

3.3.2 不同算法比较

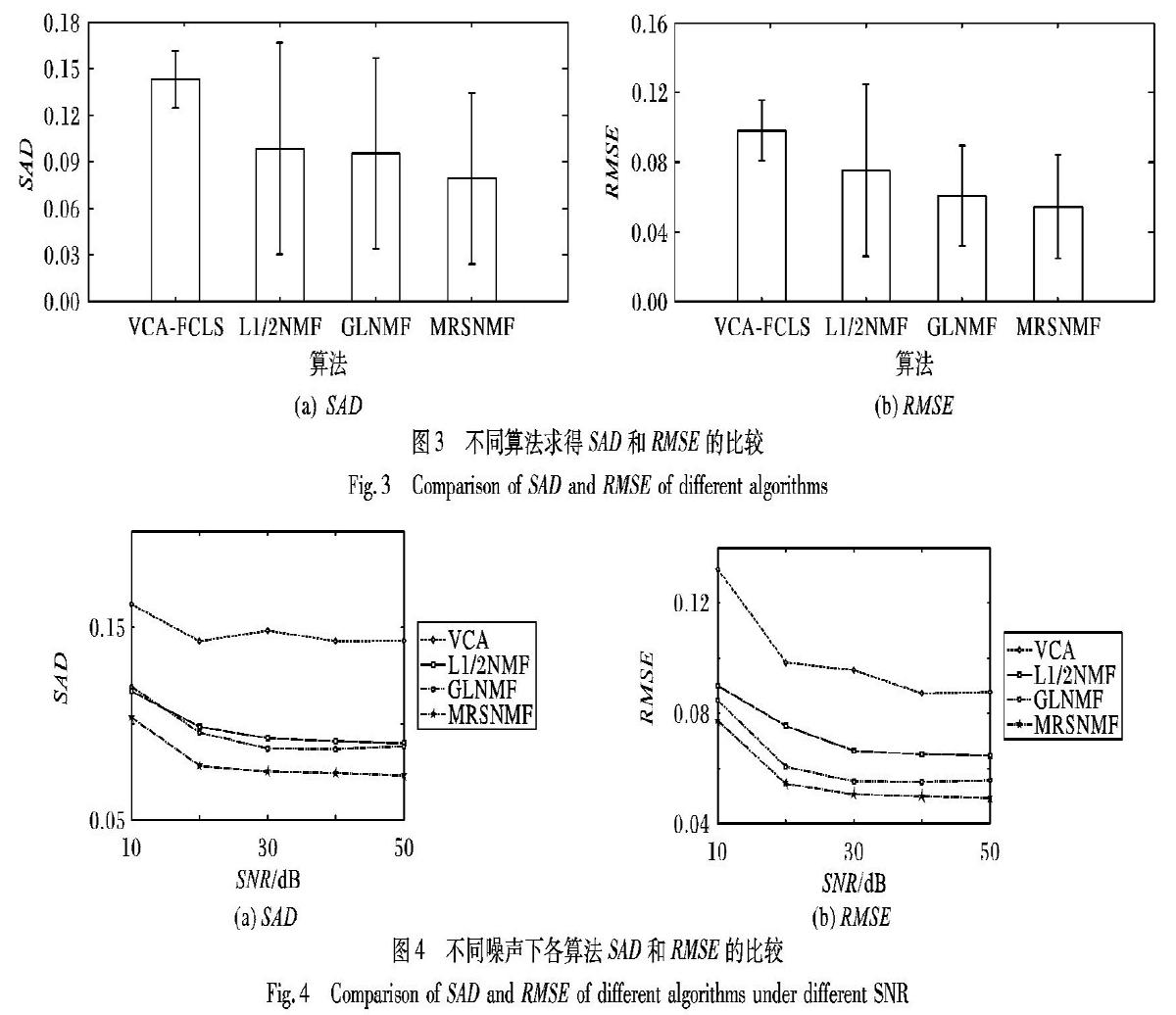
将本文MRS-NMF算法同其他流行的混合像元分解方法就解混的性能进行了比较，对比算法包括：顶点成分分析全约束最小二乘法L1/2NMF[11]、GLNMF[13]。在本实验中，设置信噪比SNR=30dB，基于NMF的方法端元和丰度的初始化方法均采用随机初始化，并且在各方法的对比实验中都采用相同的初始值，实验中的其他参数与上文一致。首先按照算法1中的步骤求解出端元矩阵和丰度矩阵，然后根据式（14）和（15）计算出SAD和RMSE。图3为上述模拟数据重复20次实验时，不同方法所求得的SAD和RMSE的均值和方差。从图3可看出：无论是SAD还是RMSE，VCA-FCLS算法分解性能最差，这是因为VCA算法在纯像元存在时，才能提取出端元，而本实验则不存在纯像元。另一方面，VCA-FCLS算法的标准差比基于NMF的算法都要小，稳定性相对较好，这是因为基于NMF的算法本身不存在全部最优解，且算法对初始值依赖性较大。最后比较所有方法，发现本文MRS-NMF算法分解精度最好，说明新方法有效地利用了高光谱图像的空间信息和光谱信息以及丰度的稀疏性从而提高了分解效果。最后在所有基于NMF的方法中，本文MRS-NMF算法的标准差最小，这也说明本文算法比其他算法拥有较好的稳定性。

3.3.3 抗噪性能比较

本部分通过向模拟数据添加不同程度的噪声，以测试各方法的抗噪能力。实验中的其他参数与上文一致，仅改变所添加噪声的信噪比SNR，以10dB为步长，将SNR从10dB增加到40dB以及考虑SNR为无穷大（无噪声）的情况。采用同样的方法，按照算法1中的步骤以及式（14）和（15）计算出SAD和RMSE。图4为不同信噪比SNR下各算法的分解结果，其中基于NMF的方法，采用了随机初始化方法，并且在各对比实验中初始值保持一致，所有的算法均取运行20次后的平均值。从图4可看出：VCA-FCLS算法的分解效果最差，同样是因为模拟图像中不存在纯像元，而基于NMF的方法则不需要纯像元的存在，效果较VCA-FCLS均要好。同时随着信噪比的增加，各算法的解混性能均趋于好转，且本文MRS-NMF算法比其他几种方法要好，这也说明本文算法结合空间和光谱信息以及丰度的稀疏性后具有较好的抗噪性能。

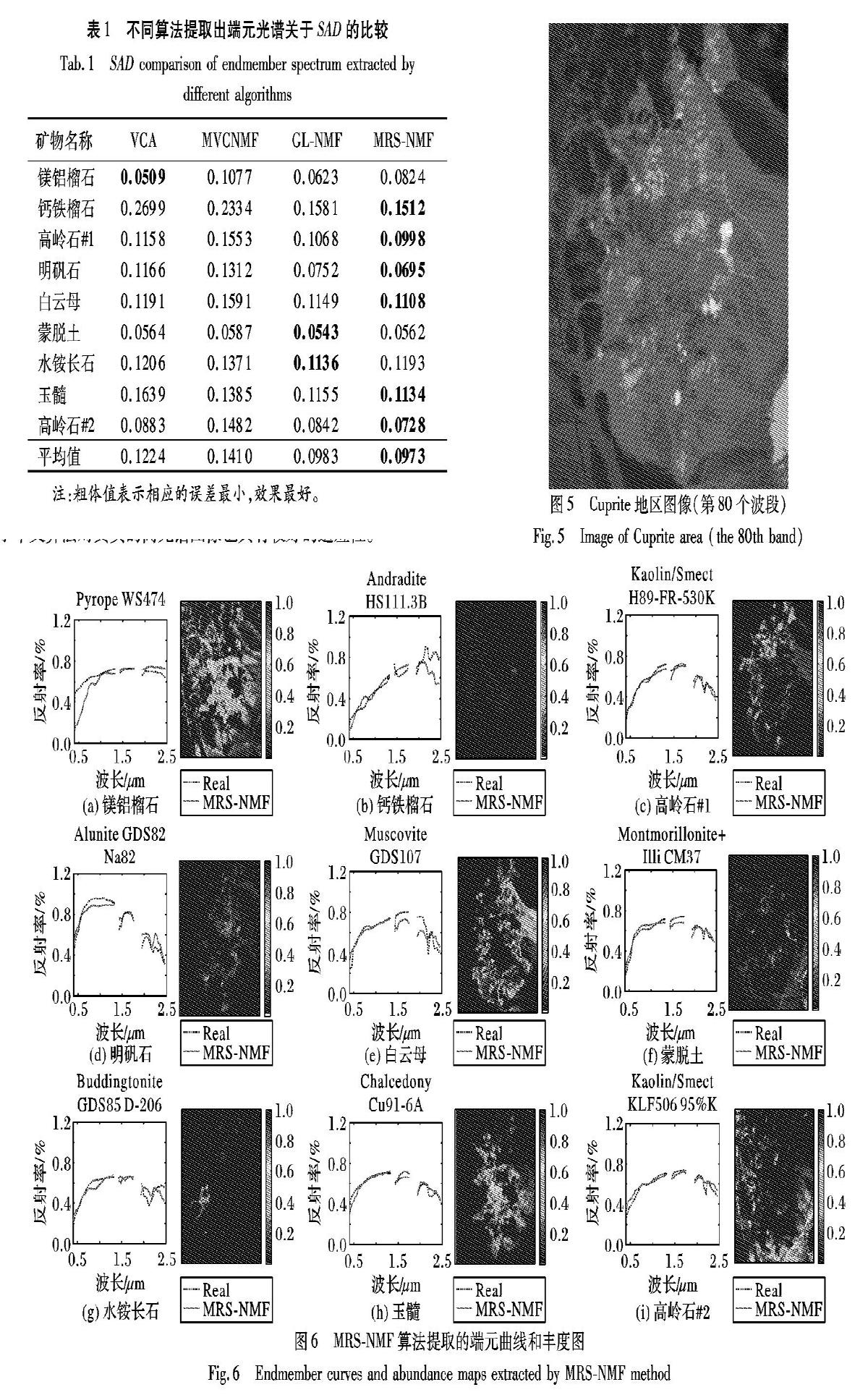
采集的美国内华达州Cuprite区域图像来完成这一实验。该区域各类矿物分布错综复杂，混合现象十分严重，被广泛应用于混合像元分解领域[9-14，19]。原始图像包含了224个光谱波段，波长范围为0.37～2.48μm，光谱分辨率为10nm，去除那些低信噪比以及被水蒸气吸收的波段，在本实验中仅采用188个波段做后续的处理。同时，为了减轻计算负担，提高运算效率，本实验仅计算大小为250×191的子图像区域。图5为该子图像的第80个波段。

根据虚拟维度算法[20]以及目前现有知识对该地区矿物的分析情况[9，19]，选择端元个数为9。同时，在本实验中采用VCA-FCLS方法作为端元矩阵和丰度矩阵的初始化方法，以期提高计算速度。最大迭代次数设置为3000作为迭代停止条件，按照算法1中的步骤求解出端元矩阵和丰度矩阵。图6列出了本文MRS-NMF算法所求解出来的端元曲线与光谱库中参考端元曲线的对比情况以及分解后的丰度图像。从图6中可以看出，估计的端元曲线和参考曲线非常相近，另外和已经公布的丰度参考图像（http：//speclab.cr.usgs.gov/PAPERS/tetracorder/FIGURES/fig9b.cuprite95.tgif.2.2um_map.gif）相比，本文算法在豐度图像上也获得了较好的效果。求解的端元和参考端元之间的定量比较如表1所示。

由于MVCNMF只考虑了端元的几何信息，而忽略了流形结构信息，故也加入本次实验进行对比。

從表1也可看出，本文MRS-NMF算法对大多数矿物都有较好的分解性能，同时误差的平均值最小，精度最高。这也说明本文算法结合光谱和空间信息以及丰度稀疏性后能够提高混合像元分解的性能，同时也说明了本文算法对真实的高光谱图像也具有较好的适应性。

4 结语

本文提出了一种基于超像素的流形正则化稀疏约束NMF混合像元分解算法——MRS-NMF。该算法基于NMF模型，不需要原图像存在纯净像元，并且可以同时得到端元和丰度。MRS-NMF算法利用超像素分割来获取高光谱图像的流形结构信息，同时在目标函数中有效结合了流形结构信息和丰度图像稀疏特性。最后合成的模拟图像和真实的高光谱图像实验结果表明，本文算法较传统混合像元分解具有更好的分解效果和抗噪性能。在下一步的研究工作中，将根据图像的本身特性，设置算法自动确定超像素的个数，从而提升混合像元分解的效率。

参考文献（References）

[1] 徐晨光， 邓承志， 朱华生. 近似稀疏约束的多层非负矩阵分解高光谱解混[J]. 红外与激光工程， 2018， 47（11）： 257-265. （XU C G， DENG C Z， ZHU H S. Approximate sparse regularized multilayer NMF for hyperspectral unmixing[J]. Infrared and Laser Engineering， 2018， 47（11）： 257-265.）

[2] 王瀛， 何欣， 左方. 基于最大整体包容度约束非负矩阵分解的高光谱遥感图像混合像元分析算法[J]. 光子学报， 2018， 47（3）： 136-144. （WANG Y， HE X， ZUO F. Mixed data analysis algorithm based on maximum overall coverage constraint nonnegative matrix factorization for hyperspectral image[J]. Acta Photonica Sinica， 2018， 47（3）： 136-144.）

[3] NASCIMENTO J M P， DIAS J M B. Vertex component analysis： a fast algorithm to unmix hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing， 2005， 43（4）： 898-910.

[4] BOARDMAN J W， KRUSE F A， GREEN R O. Mapping target signatures via partial unmixing of AVIRIS data [EB/OL]. [2019-01-10]. http：//www.hgimaging.com/PDF/boardman95.PDF.

[5] WINTER M E. N-FINDR： an algorithm for fast autonomous spectral end-member determination in hyperspectral data[J]. Proceedings of the SPIE， 1999， 3753： 266-275.

[6] PLAZA A， MARTINEZ P， PEREZ R， et al. Spatial/spectral endmember extraction by multidimensional morphological operations[J]. IEEE Transactions on Geoscience and Remote Sensing， 2002， 40（9）： 2025-2041.

[7] HEINZ D C， CHANG C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing， 2001， 39（3）： 529-545.

[8] WANG J， CHANG C. Applications of independent component analysis in endmember extraction and abundance quantification for hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing， 2006， 44（9）： 2601-2616.

[9] MIAO L， QI H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing， 2007， 45（3）： 765-777.

[10] WANG N， DU B， ZHANG L. An endmember dissimilarity constrained non-negative matrix factorization method for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2013， 6（2）： 554-569.

[11] QIAN Y， JIA S， ZHOU J， et al. Hyperspectral unmixing via L1/2 sparsity constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing， 2011， 49（11）： 4282-4297.

[12] WU C， SHEN C. Spectral unmixing using sparse and smooth nonnegative matrix factorization[C]// Proceedings of 21st International Conference on Geoinformatics. Piscataway： IEEE， 2013： 1-5.

[13] LU X， WU H. Manifold regularized sparse NMF for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing， 2013， 51（5）： 2815-2826.

[14] RAJABI R， GHASSEMIAN H. Sparsity constrained graph regularized NMF for spectral unmixing of hyperspectral data[J]. Journal of the Indian Society of Remote Sensing， 2015， 43（2）： 269-278.

[15] CAI D， HE X， HAN J， et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2011， 33（8）： 1548-1560.

[16] BELKIN M， NIYOGI P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]// Proceedings of the 14th International Conference on Neural Information Processing Systems. Cambridge， MA： MIT Press， 2001： 585-591.

[17] LEE D D， SEUNG S H. Learning the parts of objects by non-negative matrix factorization[J]. Nature， 1999， 401（6755）： 788-791.

[18] LIU M Y， TUZEL O， RAMALINGAM S， et al. Entropy rate superpixel segmentation[C]// Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2011： 2097-2104.

[19] LI D G， LI S T， LI H L. Hyperspectral image unmixing based on sparse and minimum volume constrained nonnegative matrix factorization[C]// Proceedings of the 6th Chinese Conference on Pattern Recognition. Berlin： Springer， 2014： 44-52.

[20] CHANG C， DU Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing， 2004， 42（3）： 608-619.