基于拼接缝自适应消除和全景图矫直的快速图像拼接算法

杨春德 成燕菲

摘 要：针对图像拼接存在色差过渡不均匀、图像倾斜扭曲及拼接效率低的现象，提出一种基于拼接缝自适应消除和全景图矫直的快速图像拼接算法。首先，用尺度不变特征变换（SIFT）提取图像指定区域特征点并用双向K近邻（KNN）算法进行图像配准，有效提高算法效率;其次，利用动态规划思想提出自适应公式找到最优拼接缝并用图像融合算法对其自适应消除，解决拼接缝色差过渡不均匀问题;最后，针对累积拼接误差形成全景图倾斜的现象，利用边缘检测算法提出自适应拟合四边形矫直模型，把原始全景图矫直为一个全新的全景图。所提算法与分块图像拼接和二叉树图像拼接算法相比，图像质量提升了5.84%～7.83%，拼接时间仅为原来的50%～70%。

实验结果表明，该算法不仅通过自适应更新机制减少不同图像背景下拼接缝色差过渡不均匀的现象，从而提高了图像质量;而且提高了拼接效率，降低了全景图倾斜扭曲程度。

关键词： 尺度不变特征变换;最优拼接缝;图像融合;自适应消除;图像矫直

中图分类号：TP391.41

文献标志码：A

Abstract：Aiming at the phenomenon that image mosaic， to a certain extent， has uneven chromatic aberration， distortion and low efficiency， an adaptive elimination of image stitching seam and panorama alignment based fast image mosaic algorithm was proposed. Firstly， the Scale-Invariant Feature Transform （SIFT） was used to extract feature points of the specified area of the image and image registration was performed by using bidirectional K-Nearest Neighbor （KNN） algorithm， effectively improving the algorithm efficiency. Secondly， focusing on the uneven chromatic aberration transition of stitching seam， an adaptive formula for finding the optimal stitching seam was proposed based on dynamic programming， and then the seam was adaptively eliminated by image fusion. Finally， for the phenomenon of panoramic tilt caused by accumlated stitching error， an adaptive fitting quadrilateral alignment model based on edge detection algorithm was proposed to make the original panorama into a completely new panorama. Compared with the image mosaic algorithm based on block and the image mosaic algorithm based on binary tree， the proposed algorithm has the image quality improved by 5.84%-7.83% and the stitching time shortened to only 50%-70% of the original. Experimental  results show that the proposed algorithm not only reduces the unevenness of chromatic aberration transition of stitching seam in different image backgrounds through adaptive update mechanism， so as to improve the image quality， but also increases the stitching efficiency and reduces the distortion degree of panorama.

Key words：  Scale-Invariant Feature Transform （SIFT）; optimal stitching seam; image fusion; adaptive elimination; image alignment

0 引言

图像拼接技术[1]是将同一场景下数幅有序且有重复区域的图像拼接成一幅全景图，在无人机航拍、遥感图像等领域应用广泛。图像拼接一般分为特征提取、图像配准和图像融合三个部分。

目前，在图像处理领域，国内外专家都做了大量的研究。其中，郑悦等[2]提出邻域最短距离法寻找最佳拼接缝算法，仍没能解决拼接缝两侧过渡不均的问题;Wei等[3]提出快速多波段融合算法，实现对高空间低光谱分辨率图像和低空间高光谱分辨率图像的融合，仍存在拼接缝明显问题;Tong等[4]提出基于剪切和小波變换的异构传感器网络压缩感知图像融合算法，可以在低采样率下获得理想融合结果;Laraqui等[5]提出应用于图像拼接的多尺度图像预处理算法，可以校正图像之间的尺度差异，以减少异常值和对齐误差;邹佳彬等[6]提出的基于提升静态小波变换与联合结构组稀疏表示的多聚焦图像融合算法，可以较好保留图像的纹理与边缘等细节信息，融合图像效果比较好。

本文为提高图像质量和拼接效率，同时降低图像扭曲误差，提出一种基于最优拼接缝自适应消除和全景图矫直的快速图像拼接算法。

该算法改进了SIFT（Scale Invariant Feature Transform， SIFT）算法[7]，只提取图像指定区域的特征，并使用双向K近邻（K-Nearest Neighbor， KNN）算法剔除误匹配特征点，完成图像配准;然后，在图像重叠区域运用动态规划思想寻找最优拼接缝，再对最优拼接缝限定区域进行多分辨率拉普拉斯融合;最后，建立自适应拟合四边形矫直模型，可以自适应地对全景图进行误差矫直，有效消除扭曲现象，完成图像拼接。

1 图像配准

特征配准是两幅含有重叠区域图像的特征点进行配准，首先要提取特征点。传统SIFT算法提取特征点由四个关键步骤组成：尺度空间极值检测[8];定位关键点;确定关键点方向;生成特征描述子。基于传统SIFT算法因提取整幅图像特征导致算法计算量大，并易造成后续匹配错误和计算冗余。本文改进SIFT算法，在尺度空间进行极值检测时，以数像素点的方式只检测图像指定区域特征点，缩短图像检测范围，在保证特征提取准确度的同时，有效提高时间效率。

SIFT特征提取后，分别对参考图像和目标图像建立K-D树（K-Dimensional Tree），并分别取其中一个为参考进行KNN匹配，提取两次匹配操作的公共匹配对作为初始匹配。获得初始匹配结果后，采用随机采样一致性（RANdom SAmple Consensus， RANSAC）算法[9-10]剔除外点，保留内点，降低误匹配率，并估算图像之间的仿射变换矩阵。初始匹配得到的匹配对中随机选取a对点对集合，θ′为图像旋转角度，u、v为图像沿x轴与y轴方向的水平位移。经过多次迭代，估算出矩阵模型H的参数，如式（3）：

2 最优拼接缝的自适应消除图像融合

传统的图像融合算法对配准后的多幅有序图像直接融合，会产生十分明显的拼接缝并且出现色差过渡不连续和伪影的现象[11-12]。因此，本文提出一种最优拼接缝自适应消除的图像融合算法。

寻找最优拼接缝[13]的常用算法有狄克斯特拉算法、贪婪算法等。这些算法不能自适应地应用于各种场景，并且时间复杂度较高无法满足实时拼接的需求。本文提出一种基于动态规划思想寻找最优拼接缝的算法，可以有效解决这个问题。本文算法核心是扫描图像重叠区域的像素信息，找到每行像素点在重叠部分图像色差最小且结构与周围像素点最相似的位置，即计算当前像素点的能量值是否为每行像素点的最小值。能量值的取值与重叠部分图像的色差和纹理差有关。这些位置的像素点集合，就是要找的最优拼接缝。

找到最优拼接缝后对待拼接图像直接拼接，会出现拼接缝的痕迹。为了消除拼接缝，需要对拼接图像进行图像融合。本文使用改进的最优拼接缝拉普拉斯图像融合算法，对融合区域ξ进行限制，消除伪影和拼接缝，提高融合效率和图像质量。

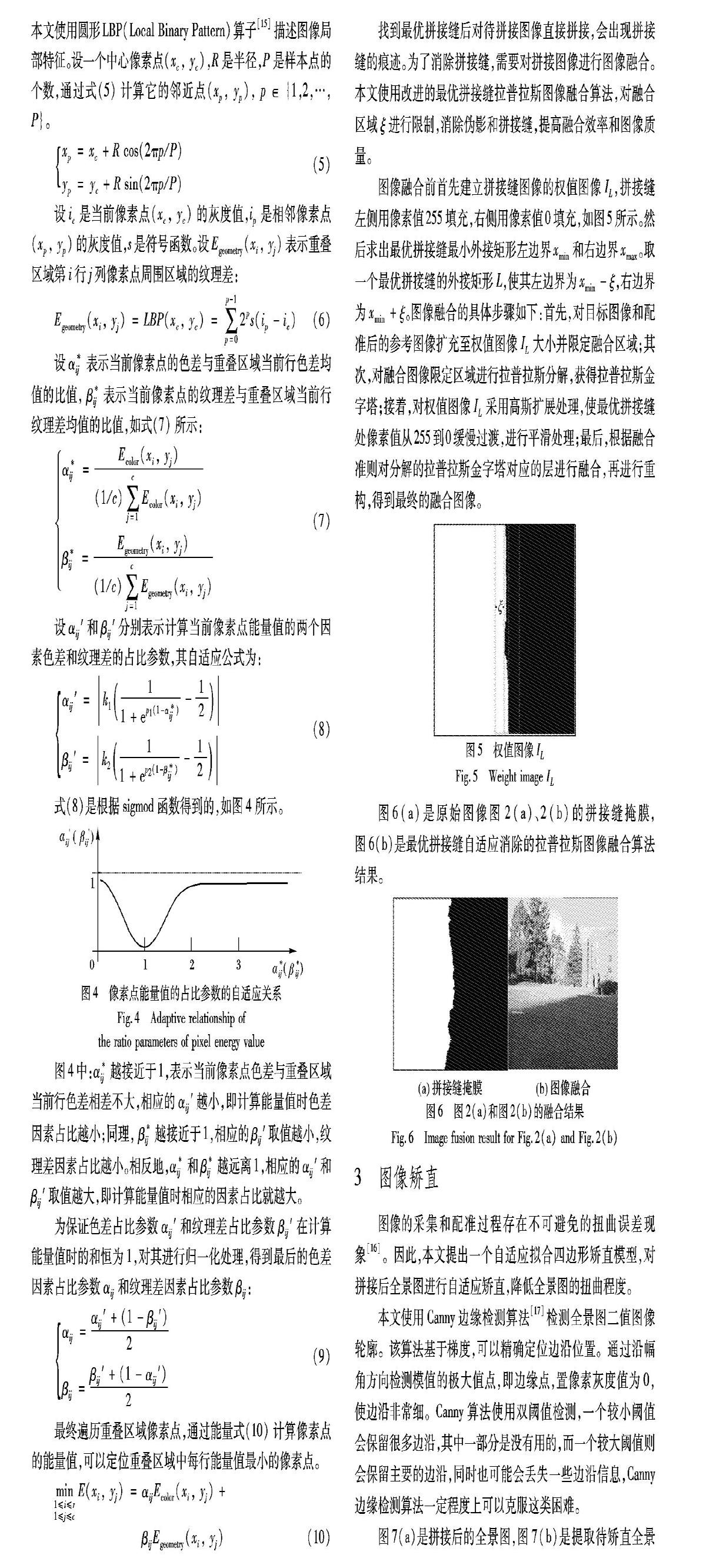
图像融合前首先建立拼接缝图像的权值图像IL，拼接缝左侧用像素值255填充，右侧用像素值0填充，如图5所示。然后求出最优拼接缝最小外接矩形左边界xmin和右边界xmax。取一个最优拼接缝的外接矩形L，使其左边界为xmin-ξ，右边界为xmin+ξ。图像融合的具体步骤如下：首先，对目标图像和配准后的参考图像扩充至權值图像IL大小并限定融合区域;其次，对融合图像限定区域进行拉普拉斯分解，获得拉普拉斯金字塔;接着，对权值图像IL采用高斯扩展处理，使最优拼接缝处像素值从255到0缓慢过渡，进行平滑处理;最后，根据融合准则对分解的拉普拉斯金字塔对应的层进行融合，再进行重构，得到最终的融合图像。

3 图像矫直

图像的采集和配准过程存在不可避免的扭曲误差现象[16]。因此，本文提出一个自适应拟合四边形矫直模型，对拼接后全景图进行自适应矫直，降低全景图的扭曲程度。

本文使用Canny边缘检测算法[17]检测全景图二值图像轮廓。该算法基于梯度，可以精确定位边沿位置。通过沿幅角方向检测模值的极大值点，即边缘点，置像素灰度值为0，使边沿非常细。Canny算法使用双阈值检测，一个较小阈值会保留很多边沿，其中一部分是没有用的，而一个较大阈值则会保留主要的边沿，同时也可能会丢失一些边沿信息，Canny边缘检测算法一定程度上可以克服这类困难。

将提取的边缘拟合成四条直线，形成一个近似四边形，如图8（a）是基于图7（b）全景图拟合的四边形。设θ是图像矫直角度，θi（i=1，2）是拟合四边形中两条水平向边的倾斜角度，li.x、li.y是两条水平向边上的任意一点坐标值。θ的取值为：

本文具体算法步骤如下：

输入 有重叠区域的有序图像序列S（S1，S2，…，SN）。

输出 一幅拼接并矫直的全景图。

步骤1 针对拼接图像Si和Si+1（i∈[1，N-1]），图像配准。

1）判断相邻图像是目标图像还是参考图像，并确定m的取值0.4j，得到限定区域[i，m]。

2）对限定区域提取特征点，使用双向KNN算法，计算欧氏距离，将初始匹配特征点集合和数目保存在数组FeatureSet和NumF中。

3）使用RANSAC算法剔除误匹配后，计算Si和Si+1之间的仿变换模型，保存在数组HF中。

4）返回步骤1）继续下一组相邻图像的图像配准，直到完成所有图像序列间的配准为止。

步骤2 根据数组HF通过式（3）计算仿射变换矩阵H，使目标图像与参考图像在相同坐标系下。

步骤3 利用式（4）找到最优拼接缝并使用多分辨率拉普拉斯融合算法进行图像融合。

步骤4 转到步骤2执行下一幅图像拼接直到图像序列S只有一幅图像为止。

步骤5 对拼接后全景图使用边缘检测算法，并利用式（11）和（12）对全景图进行矫直，得到矫直后的全景图。

算法流程如图9所示。

4 实验与结果分析

4.1 主观评价

本文算法对多个场景图像进行图像拼接和矫直实验，实验在CPU为Intel i5处理器、内存为4GB的Windows 7系统下完成，实验环境是Visual Studio （OpenCV 2.4.9）。实验中的参数a=3。

图11（a）、图13（a）和15（a）是基于分块图像拼接算法的结果[18]，图11（b）、13（b）和15（b）是基于二叉树图像拼接算法的结果[19]，图11（c）、13（c）和15（c）是本文改进算法的拼接结果。从图11的实线方框以及放大细节图中的实线圆框可以明显看出，其他两种算法得到的拼接图像仍存在明显的拼接痕迹，甚至出现图像扭曲、失真的现象，而本文算法对拼接缝周围的色差过渡有显著效果。因此，从视觉上明显看出，本文算法得到的全景图更能够满足人们对图像的视觉要求。

4.2 实验参数及客观评价

为了更客观地反映本文算法的优越性，通过计算图像的统计参数获得相对客观的量化指标，对图像拼接算法进行客观评价[20-21]。

全景图扭曲程度越大，全景图中无用黑色像素随之增多，信息比参数越小。

要使式（8）中的函数在[0，2]以α*ij（β*ij）=1为对称轴，就要使式（8）中的参数p1=4， p2=4，如图4所示。同时，经过多次实验，参数k1=1.8、k2=1.7时图像清晰度最好，结果对比如表1所示

从表2可明显看出，本文算法在全景图的清晰度、倾斜角度和信息比方面都有较为明显的进步，

而且随着图像数据集的增加，

这些优势会越明显。在本文图像数据集中，与基于分块的图像拼接算法和基于二叉树的图像拼接算法对比，清晰度比前者平均提高7.83%，比后者平均提高5.84%;倾斜度比前者平均降低1.57°，比后者平均提稿1.14°;信息比比前者平均提升2.54%，比后者平均提高2.87%。因此，本文的拼接算法改善了图像拼接中的扭曲现象，同时提高了拼接后全景图的质量。

本文算法的运行时间由三个阶段组成：

图像配准、图像融合和图像矫直。由式（2）可知，图像配准的时间效率λ与图像分辨率和限定提取特征的区域参数m有关;由式（10）以及融合范围可知，图像融合的时间效率与图像分辨率和限定融合范围参数ξ有关;由式（11）和（12）可知，图像矫直的时间效率与全景图分辨率有关。因此，本文算法的时间效率是由图像

分辨率以及参数m和ξ决定的，ξ的经验阈值为30。而本文算

法是与其他两种算法的时间进行比对，因此，针对同样的图像数据集，图像分辨率的因素不考虑在内，m的取值在参考了黄金分割比0.618以及对本文图像数据集的分析，考虑m的取值范围在0.35j～0.55j，经过多次实验，取得最优经验阈值0.4j，实验效果最好，见表3。同时，通过式（2）计算得到的λ可知，配准算法的时间可以缩短近60%。图16是本文算法与其他两种对比算法的时间对比。

从表3可以看到，虽然提取整幅图像的SIFT特征点个数比较多，但对比提取指定区域图像的SIFT特征点，它们的匹配对数是相似的，但时间花销明显少很多，甚至经过RANSAC剔除誤匹配后本文算法的匹配率更高，平均在87%左右。结合图16的全景图拼接时间的对比，可以明显看出，虽然本文算法的图像融合时间对比其他算法会有小幅度增加，但图像配准的时间在拼接算法中的时间占比是最重的。因此，本文算法比传统的SIFT特征匹配方法具有更强的鲁棒性。拼接算法消耗的时间是分块图像拼接算法的70%，是二叉树图像拼接算法的50%。

5 结语

在传统的图像拼接算法基础上，本文算法首先限定了SIFT特征的提取区域，在保证特征匹配准确率的同时，大幅缩短了算法的时间。同时，在此基础上提出了基于最优拼接缝的自适应消除图像融合算法，通过提出的自适应能量公式找到最优拼接缝并进行消除，有效地解决了伪影以及模糊像素点导致的色差问题。最后，对拼接后的全景图进行拟合四边形矫直，进一步改善图像失真问题。实验结果表明，本文算法有效提高了图像拼接质量和图像清晰度，有效保留了全景图信息;同时，提高了算法效率，实现了序列图像快速拼接。

参考文献（References）

[1] ALCANTARILLA P F， NUEVO J， BARTOLI A. Fast explicit diffusion for accelerated features in nonlinear scale spaces[C]// Proceedings of the 24th British Machine Vision Conference. Durham： BMVA Press， 2013： 1-11.

[2] 郑悦， 程红， 孙文邦. 邻域最短距离法寻找最佳拼接缝[J]. 中国图象图形学报， 2014， 19（2）： 227-233. （ZHENG Y， CHENG H， SUN W B. Finding an optimal seam-line through the shorted distance in the neighborhood[J]. Journal of Image and Graphics， 2014， 19（2）： 227-233.）

[3] WEI Q， DOBIGEON N， TOURNERET J. Fast fusion of multi-band images based on solving a Sylvester equation[J]. IEEE Transactions on Image Processing， 2015， 24（11）： 4109-4119.

[4] TONG Y， CHEN J. Compressive sensing image fusion in heterogeneous sensor networks based on shearlet and wavelet transform[J]. EURASIP Journal on Wireless Communications and Networking， 2017， 2017： 52.

[5] LARAQUI A， SAAIDI A， SATORI K. MSIP： multi-scale image pre-processing method applied in image mosaic[J]. Multimedia Tools and Applications， 2018， 77（6）： 7517-7537.

[6] 鄒佳彬， 孙伟. 基于提升静态小波变换与联合结构组稀疏表示的多聚焦图像融合[J]. 计算机应用， 2018， 38（3）： 859-865. （ZOU J B， SUN W. Multi-focus image fusion based on lifting stationary wavelet transform and joint structural group sparse representation[J]. Journal of Computer Applications， 2018， 38（3）： 859-865.）

[7] BROWN M， LOWE D G. Automatic panoramic image stitching using invariant features[J]. International Journal of Computer Vision 2007， 74（1）： 59-73.

[8] MIKOLAJCZYK K， SCHMID C. An affine invariant interest point detector[C]// Proceedings of the 2002 European Conference on Computer Vision， LNCS 2350. Berlin： Springer， 2002： 128-142.

[9] FISCHLER M A， BOLLES R C. Random sample consensus： a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM 1981， 24（6）： 381-395.

[10] WAINE M， ROSSA C， SLOBODA R， et al. 3D shape visualization of curved needles in tissue from 2D ultrasound images using RANSAC[C]// Proceedings of the 2015 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2015： 4723-4728.

[11] TANG Y， SHIN J， LIAO H C. De-ghosting method for image stitching[J]. International Journal of Digital Content Technology & Its Applications， 2012， 6： 17-24.

[12] ZHANG B， LIU Q， IKENAGA T. Ghost-free high dynamic range imaging via moving objects detection and extension[C]// Proceedings of the 2015 Asia-Pacific Signal and Information Processing Association Summit and Conference. Piscataway： IEEE， 2015： 459-462.

[13] HUANG C， LIN S， CHEN J. Efficient image stitching of continuous image sequence with image and seam selections[J]. IEEE Sensors Journal， 2015， 15（10）： 5910-5918.

[14] 方贤勇， 潘志庚， 徐丹. 图像拼接的改进算法[J]. 计算机辅助设计与图形学学报， 2003， 15（11）： 1362-1365. （FANG X Y， PAN Z G， XU D. An improved algorithm for image mosaics[J]. Journal of Computer-Aided Design & Computer Graphics， 2003， 15（1）： 1362-1365.）

[15] AHONEN T， HADID A， PIETIKINEN M. Face recognition with local binary patterns[C]// Proceedings of the 2004 European Conference on Computer Vision， LNCS 3021. Berlin： Springer， 2004： 469-481.

[16] CHOI H C， AHN B H. Image alignment by parameter hypersurface learning[J]. Electronics Letters， 2016， 52（18）： 1526-1527.

[17] CANNY J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1986， 8（6）： 679-698.

[18] QU Z， WANG T， AN S Q， et al. Image seamless stitching and straightening based on image block[J]. IET Image Processing， 2018， 12（8）： 1361-1369.

[19] QU Z， WEI X， CHEN S. An algorithm of image mosaic based on binary tree and eliminating distortion error[J].  PLoS One， 2019， 14（1）： e0210354.

[20] 張小利， 李雄飞， 李军. 融合图像质量评价指标的相关性分析及性能评估[J]. 自动化学报， 2014， 40（2）： 306-315. （ZHANG X L， LI X F， LI J. Validation and correlation analysis of metrics for evaluating performance of image fusion[J]. Acta Automatica Sinica， 2014， 40（2）： 306-315.）

[21] 黄学优， 张长江. 双树复小波域的MRI图像去噪[J]. 中国图象图形学报， 2016， 21（1）： 104-113. （HUANG X Y， ZHANG C J. MRI denoising based on dual-tree complex wavelet transform[J]. Journal of Image and Graphics， 2016， 21（1）： 104-113.）