求解旅行商问题的多样化搜索帝国竞争算法

陈孟辉 刘俊麟 徐健锋 李向军

摘 要：帝国竞争算法是一种局部搜索能力较强的群智能优化算法，但过度的局部搜索会导致多样性丢失并陷入局部最优。针对这一问题提出基于多样化搜索的帝国竞争算法（MSSICA）。将国家定义为一条可行解，将王国定义成四种特性不同的组合人造解方式。在搜索时使用区块机制保留各自的优势解片段，并对不同的帝国使用差异化的组合人造解方式以搜索不同解空间的有效可行解信息。在陷入局部最优时，使用多样化搜索策略注入均匀分布的可行解替换较无优势的解以提升多样性。实验结果显示，多样化搜索策略可以有效地改善帝国算法的求解多样性，并提升求解质量与稳定性。

关键词：组合性问题;人造解;帝国竞争算法;全局搜索

中图分类号：TP301.6

文献标志码：A

Abstract：  The imperialist competitive algorithm is a swarm intelligence optimization algorithm with strong local search ability， but excessive local search will lead to the loss of diversity and fall into local optimum. Aiming at this problem， an Imperialist Competitive Algorithm based on Multiple Search Strategy （MSSICA） was proposed. The country was defined as a feasible solution and the kingdoms were defined as fourmechanisms of combinatorial artificial chromosome with different characteristics. The block mechanism was used to retain the dominant solution fragment during search and differentiated mechanisms  of combinatorial artificialchromosomewas used for different empires to search the effective and feasible solution information of different solution spaces. When it come to the local optimum， the multiple search strategy was used to inject a uniformly distributed feasible solution to replace a less advantageous solution to enhance the diversity. Experimental  results show that the multiple search strategy can effectively improve diversity of the imperialist competitive algorithm and improve the quality and stability of the solution.Key words：  combinatorial problem; artificial chromosome; imperialist competitive algorithm; global search

0 引言

旅行商問题（Traveling Salesman Problem， TSP）[1-3]是经典的NP-Hard组合优化问题，它的描述如下：设一位商人需要到N个城市推销商品，依次不重复地访问每个城市，最终回到起始城市，求解其访问路线的最短回路。生活中常见的电路板布线问题、最短物流配送问题、车间调度问题等，都可抽象为TSP从而进行求解，因此研究TSP具有较高的实际价值和理论意义。

该类问题的求解主要有完全算法和近似算法两大方向。完全算法如动态规划法等可以保证搜索到最优解，但由于其时间复杂度过高，在大规模问题上往往难以满足性能要求。而近似算法如启发式算法[4-6]等只能找到近似解，不过可以在多项式时间内结束，但对于较为复杂的非线性问题，容易陷入局部最优。因此，如何有效优化启发式算法，改善其全局搜索能力，成为广大学者关注和研究的热点。

2007年Atashpaz-Gargari等[7-9]受到人类社会政治演化过程的启发，从帝国间的殖民竞争到最终称霸的过程中提出了帝国竞争算法（Imperialist Competitive Algorithm， ICA）。Forouharfard等[10]在接驳式转运问题上的实验数据显示，该算法在求解效果、收敛速度和运行时间上都比基因算法更优越，但依然存在搜索空间分布不均、搜索后期帝国多样性降低导致过早收敛等明显缺陷。针对上述问题，国内外很多学者基于帝国竞争算法提出了不同的改进方法。孟洪潮[11]采用拉丁超立方抽样改善帝国初始化阶段，引入人工蜂群算法中引领蜂与跟随蜂之间的信息反馈机制，但在迭代到一定次数后，蜜蜂容易在局部最优解的邻域附近发生停滞。Chang等[12]使用区块机制，在搜索过程中保留优势解序列区块，有效加速收敛，但优化效果有限且在大型复杂例题效果仍然不尽如人意。此类启发式算法求解组合性问题效果的关键在于算法的全局搜索与局部搜索的能力：当算法的设计偏重于局部搜索时，易导致演化的群体过度偏向局部的优势解区域，虽然可以快速提升解的质量，但过多的局部优势解将使解群体的多样性不足;如果没有避免陷入局部优化的机制，则解群体将难以获得全局范围内的其他优势解。

为改善帝国竞争算法的全局搜索性能，保留搜索过程中的优势片段构建区块，根据区块信息对不同的解群体使用不同的搜索策略，组合出不同的人造解注入母体。

本文所提出的基于多样化搜索策略的帝国竞争算法（Imperialist Competitive Algorithm based on Multiple Search Strategy， MSSICA），

可以在演化群体陷入局部优化时，保留该世代具有优势的解，注入均匀分布的可行解替换较无优势的解，以在后续世代有效地探索不同解空间的信息，改善帝国竞争算法的全局搜索能力。

1 帝国竞争算法

帝国竞争算法的基本假设：在ICA中，每一个国家代表一个可能的候选解，国家的强弱则由解的优劣定义。根据各个国家的兴盛程度可将国家分为帝国与殖民地两大类，每一个殖民地隶属于某一个帝国。王國由一个帝国和其控制的所有殖民地构成，每一个殖民地的国力受到所属帝国的统治影响而日益强盛，即同化作用。若殖民地的国力高过所属帝国的国力，该殖民地就会取代原本的所属帝国成为新的帝国，而原先的帝国则沦为殖民地。

帝国彼此之间也会互相竞争，王国中最弱的殖民地被其他帝国抢夺，即竞争作用。

当帝国内没有殖民地时，代表该帝国已经灭亡。如此重复帝国竞争，帝国个数会逐渐减少，直至剩下最后一个帝国，此帝国为ICA所搜索的最优解。

帝国竞争算法的主要步骤如下： 1）国家初始化。定义国家为要优化的目标变量值数组：

通常，在遗传算法中，这个数组被称为染色体。在N维优化变量问题中，国家是N维数组，代价函数定义为：

1）为了提高帝国竞争算法的收敛速度，采用区块机制挖掘出有效的区块，即通过保留搜索过程中有效的可行解片段以保留优势信息。

2）定义四种不同的组合人造解（Artificial Chromosome， AC）的机制，即根据概率模型所提供的信息，使用不同的策略人工产生解，以避免陷入局部最优，增加母体中可行解的多样性。

3）将国家定义为一条可行解，即一个满足要求的城市序列。将王国定义成四种特性不同的组合人造解方式，将母体划分成四个不同的王国。每一个王国会分布在不同的解空间上，形成四个不同的搜寻范围。初始的四个王国会分配到相同数量的殖民地，且各王国会依照特定组合人造解机制，通过竞争作用，占领更多殖民地创造多样性母体以供竞争。

4）根据高竞争优势群体的概率信息，改变搜索解的方向进行全局搜索，有效拓展解空间，提高求解的质量与多样性。

2.1 概率模型

为了能有效地利用帝国竞争算法搜索过程中的可行解信息，本文根据两个城市的相连关系构建优势矩阵。根据优势矩阵在世代迭代中挖掘出区块信息，并根据适应度更新优势矩阵。

构建优势矩阵：首先将优势矩阵初始值设为0，将当前世代母体中的解依照适应度函数值升幂排列挑选优秀解集合μ，用μ更新优势矩阵，将每条解在路径上存在存在相邻关系的城市记录到优势矩阵，且所对应的位置累加1。

其中：Xkij表示解序列的路径中的城市相连关系;i与j代表城市序号（i≠j），i， j=1，2，…，n（n代表城市数目）;k代表解序列的号码;m代表被选出用来更新矩阵的解的数目;t代表目前世代数。因本文的问题是对称路线的旅行商问题，故Cij（t）=Cji（t），优势矩阵是对称型矩阵。

2.2 区块挖掘与组合人造解

在经典帝国竞争算法的演化过程中，各个国家通过竞争作用和同化作用会不断出现可行解片段，这些固定出现的可行解片段往往就是具有优势的可行解片段。为了加速收敛，本文引入区块概念，即在演化过程中具有较高适应度函数值的可行解片段，对任一可行解可记为S={X1，X2，…，Xn}，区块可表示为任一Xij=1（i， j=1，2，…，n）且为连续序列。使用区块机制其主要目的是在迭代时保留高适应度函数值的片段，以此减少迭代次数从而显著提高搜索效率。

区块挖掘是根据优势矩阵随机选择一个起始城市，以起始城市为出发点，将优势矩阵转换成概率，任意概率大于阈值的路径记为有效路径。若所有城市概率均小于阈值，则以路径最短的记为有效路径。根据目前可供挑选的有效路径，以轮盘选择法挑选一条路径作为本次产生的区块。

挖掘出区块后将这些具有高竞争优势的信息结合为人造解。本文采用四种不同的组合人造解机制，通过将人造解注入母体来提高求解质量。

四种方式的具体描述如下：

方式一 使用轮盘选择法根据优势矩阵的概率选择。首先，随机选择初始城市，其余位置根据优势矩阵的概率用轮盘选择法选择，已被挑选进入人造解的城市不再参与选择。在区块比对部分，每当人造解添加新的城市时，会将该城市与区块数据库中的区块进行比对，若区块中含有该城市且另一与其相连的城市未被选择，则将该区块复制到人造解中;若另一与其相连的城市已被挑选到人造解，则该区块无效，从复制后的下个连接城市开始继续选择下一个城市，直到完成人造解。

方式二 根据最短距离进行选择。首先，随机产生初始城市，其余位置根据最短距离选择，已被挑选进入人造解的城市不再参与选择。在区块比对部分，采用的比对方法与方式一相同，直到完成人造解。

方式三 首先从区块数据库随机复制区块到暂存区块数据库。随机产生初始城市，其余位置根据优势矩阵的概率用轮盘选择法选择，已被挑选进入人造解的城市不再参与选择。在区块比对部分，使用暂存区块数据库对比，其他与方式一相同，直到完成人造解。

方式四 首先从区块数据库随机复制区块到暂存区块数据库。随机产生初始城市，其余位置根据最短距离选择，已被挑选进入人造解的城市不再参与选择。在区块比对部分，采用的比对方法与方式三相同，直到完成人造解。

四种组合人造解机制根据两个不同策略来筛选资源：

1）根据城市筛选。

方式一与方式三都应用轮盘选择法选择下一相连城市，以轮盘选择法选择的特性来增加人造解的多样性;

方式二与方式四都是用最短距离选择下一个相连城市，以此提高人造解的收敛速度。

2）根据资源筛选。

方式一与方式二都使用相同的资源，确保人造解的质量来取得更佳的资源;

方式三与方式四则为了避免陷入局部最优和增加解的多样性，随机采用已挖掘的区块资源。

经过人造解的注入和各国家的演化机制，母体中会产生许多新的子代，本文使用精英保留策略，筛选原始母体与子代的精英可行解，选择出新的母体进入下一世代演化。首先，将原始母体与新产生的子代，放入选择池，将选择池中所有的可行解按照适应度函数升幂排序，取前N名解组合成为新母体进入下一世代演化，其余部分使用随机可行解填充，增加母体中可行解的多样性，避免陷入局部最优化。

在本文中，王国被定义成四种特性不同的组合人造解方式，各个王国通过竞争作用抢夺殖民地。若更多的国家（可行解）使用该方式组合人造解，将更大程度地积累优势进入下一世代迭代。

2.3 多样化搜索策略

在搜索过程中，如果持续不断地按照一个方向搜索，很容易陷入局部最优，导致不断地重复搜索。因此，本文算法将母体中竞争优势较小的解舍弃，并用随机产生的可行解补充，增加母体中可行解的多样性，避免陷入局部最优化，对下一世代的区块挖掘和组合人造解具有指导作用。

在算法后期，如果持续搜索不同的区域，可能会产生较多噪声，进而影响求解方向与质量。因此当世代数达一定比例时，将清空优势矩阵，恢复到最初的搜索范围，以具有竞争优势的解来领导求解方向。

2.4 算法步骤

综上所述，本文提出的MSSICA步骤如下：

Step1 初始化解：随机产生N条初始可行解作为母体（N为母体大小），定义n为优势解的百分比。

更新概率矩阵：根据适应度函数（Fitness）

计算每一条可行解的适应度，采用前N×n个具较高优势的解更新概率模型。

Step3 区块挖掘：根据概率模型，组合出具有优势的区块。

Step4 组合人造解：使用四种方式组合人造解，产生N条人造解注入母体。

Step5 竞争作用：强盛的帝国从较弱小的帝国抢夺殖民地，筛选出母体和子代中具有竞争优势的解，成为新的母体进入下一世代演化。

Step6 判断最优解是否更新，若未更新跳转到Step7，若已经更新且若未达到结束条件则重复执行Step2～6直至满足停止条件时算法结束。

Step7 判断K是否达到阈值，达到阈值时使用多样化搜索策略更新优势矩阵，改变探索信息的范围，舍弃母体中较无优势的可行解，并随机生成可行解填充，并重复执行Step2～6。

MSSICA时间复杂度分析如下：

定義变量N为产生的初始解个数，t为演化的总世代数，X（X≤N）为优势解的数量，m为城市数量。

1）初始化解。由于此阶段仅进行一次，故T（n）=O（N）。

2）更新概率矩阵。本文求解的问题是对称型的TSP，对每个优势解需要计算m2/2次城市间距离信息，因此每个世代T（n）=O（X×m2/2）=O（X×m2）。

3）区块挖掘。区块随机从每个可能的城市挖掘，故每个世代T（n）≤O（m）。

4）组合人造解。产生数量为N的人造解，T（n）=O（N）。

5）竞争作用。重新分配帝国与帝国间的国家数量，所以每个世代T（n）=O（N）。

6）多样化搜索。假设执行了K次执行多样化搜索，且K≤T，每次将会进行再次产生N个随机解并重置概率矩阵，故T（n）=O（t×（N+1））=O（t×N）。

所以MSSICA执行t个世代的时间复杂度为：

3 对比实验

本章将通过旅行商问题编程实现进行验证，以此显示该算法对于组合性问题具有优秀的求解能力。实验环境为： Ubuntu 18.04 LTS操作系统，2 * Intel Core i9-9900k处理器，64GB内存，编程环境为Jetbrains Rider 2018.1 EAP与.NET Core 2.1。从TSPLIB95数据库（https：//wwwproxy.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/tsp）中选择21个中小型测试例题，并与BBICAHybird、BBEA、RABNET（Real-valued Antibody NETwork）[15]、SME[16]进行比较。

本文所研究的启发式算法的时间开销不会随数据复杂度呈指数增长，而是取决于演化的世代数，且本文所比较的BBICAHybird等算法中并未载明其运行时间。因此实验采用统一的参数，即母体数为100，世代数为城市数量×50，区块长度为2。

本文以误差率（Error Rate， ER）作为各算法比较的基准，且在各例题中进行30次实验并取平均值。其中误差率分为平均解误差率（Mean Error Rate，MER）和最优解误差率（Best Error Rate，BER），其计算公式分别为：

其中：Best表示该例题上使用该算法的最优解;Mean表示该例题上使用该算法的平均解;Opt代表该例题目前已知的最优解。

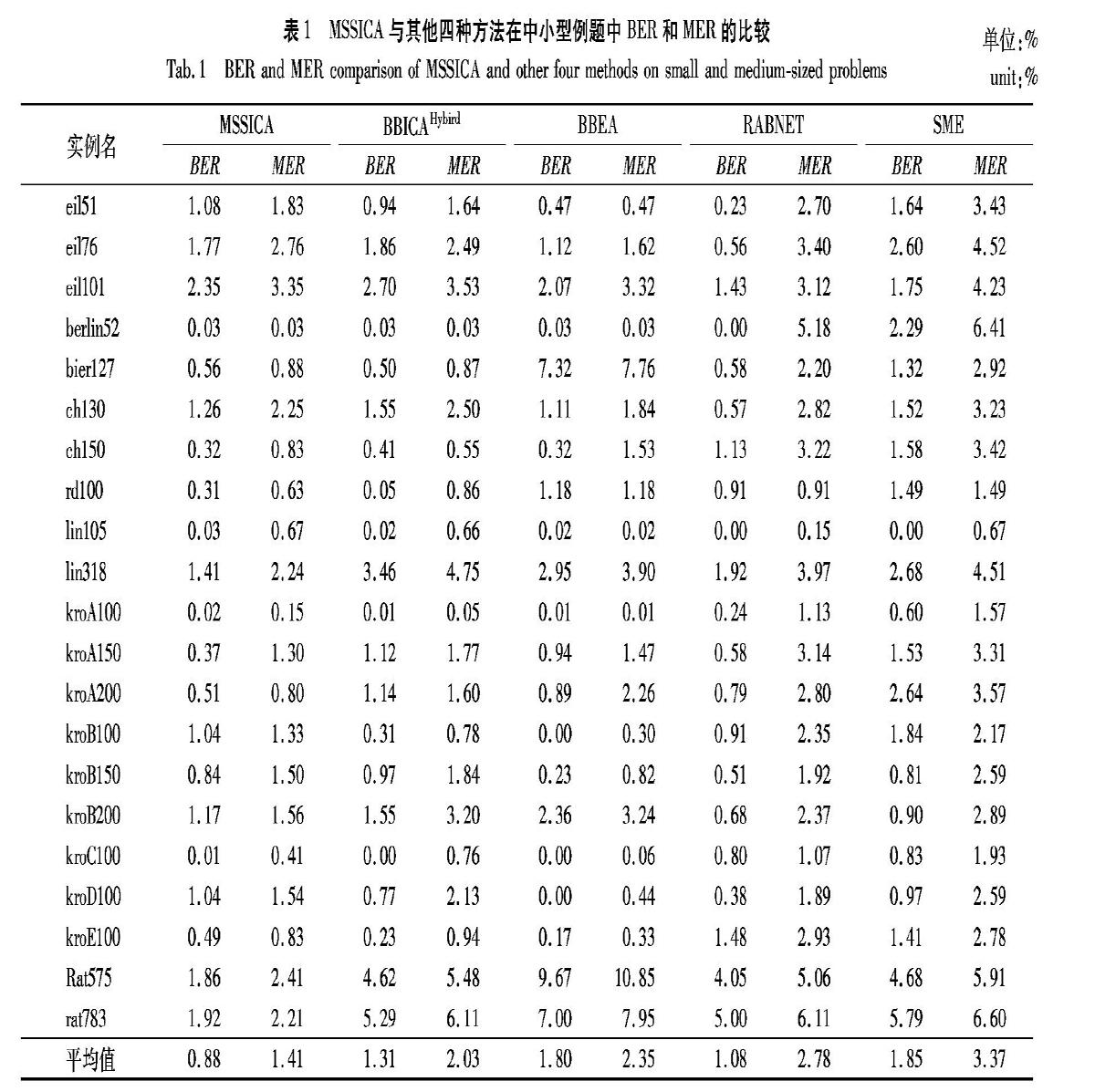
由表1可知，MSSICA在复杂度较小的例题中并不算出色;但在中型例题上，其求解能力甚为优越，以整体性能来看，求解质量明显优于其他方法。在求解稳定性方面，以30次实验次数所求得平均值的平均误差率来看，所求得的解优于其他方法，这也表明了MSSICA拥有稳定的求解能力。

在复杂度较高的例题上，若没有良好的全局搜索能力，往往容易陷入局部最优解。因此，为了验证MSSICA具有良好的全局搜索能力及稳定的求解能力，从TSPLIB数据库选择3个大型例题进行测试。

如表2的实验数据所示，MSSICA在复杂度较大的三个例题上，相较BBICAHybird及BBEA而言，在同等的时间复杂度下具有较好的求解质量和求解稳定性。

4 结语

本文改善了帝国竞争算法的国家调配机制及王国内的搜索策略，提出了多样化搜索策略。

该策略在可能陷入局部最优时保留母体中具有竞争优势的国家并舍弃母体中其他国家，然后以随机产生国家的方式填满母体。在可行解空间里由随机产生国家的方式在不同的解空间进行搜索，由概率模型及区块的方式记录正确信息，有效增加求解的多样性且不失去原有的求解质量。最后通过与同类算法比较，验证了本文所提出的基于多样化搜索策略的帝国竞争算法具备良好的全局搜索效果，也代表着本文方法可有效应用于旅行商等组合性问题。

在后续的研究中将继续关注此类问题，并使用一些新型的启发式算法求解该类问题并提高其全局搜索能力; 另一方面，将使用分布式架构，设计有效的并行算法以提高算法的效率。

参考文献（References）

[1] GOLDBERG D E， LINGLE R， Jr. Alleles， Loci， and the traveling salesman problem [C]// Proceedings of the 1st International Conference on Genetic Algorithms. Hillsdale： L. Erlbaum Associates Inc.， 1985： 154-159.

[2] ISMKHAN H， ZAMANIFAR K. Developing improved greedy crossover to solve symmetric traveling salesman problem[EB/OL].[2018-10-10]. https：//arxiv.org/ftp/arxiv/papers/1209/1209.5339.pdf.

[3] 袁豪. 旅行商问题的研究与应用[D]. 南京： 南京邮电大学， 2017： 5-6. （YUAN H. Research and application of traveling salesman problem [D]. Nanjing： Nanjing University of Posts and Telecommunications， 2017： 5-6.）

[4] ARSHAD S， YANG S. A hybrid genetic algorithm and inver over approach for the travelling salesman problem[C]// Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Piscataway： IEEE， 2010： 1-8.

[5] 王艷， 王秋萍， 王晓峰. 基于改进萤火虫算法求解旅行商问题[J]. 计算机系统应用， 2018， 27（8）： 219-225. （WANG Y， WANG Q P， WANG X F. Solving traveling salesman problem based on improved firefly algorithm[J]. Computer Systems & Applications， 2018， 27（8）： 219-225.）

[6] KIRKPATRICK S， GELATT C D， VECCHI M P. Optimization by simulated annealing[J]. Science， 1983， 220（4598）： 671-680.

[7] ATASHPAZ-GARGARI E， LUCAS C. Imperialist competitive algorithm： an algorithm for optimization inspired by imperialistic competition[C]// Proceedings of the 2007 IEEE Congress on Evolutionary Computation. Piscataway： IEEE， 2007： 4661-4666.

[8] 李明， 雷德明. 基于新型帝国竞争算法的高维多目标柔性作业车间调度[J].控制理论与应用， 2019， 36（6）：893-901. （LI M， LEI D M. Novel imperialist competitive algorithm for many-objective flexible job shop scheduling[J]. Control Theory and Applications， 2019， 36（6）：893-901.）

[9] KAVEH A， TALATAHARI S. Optimum design of skeletal structures using imperialist competitive algorithm[J]. Computers & Structures， 2010， 88（21）： 1220-1229.

[10] FOROUHARFARD S， ZANDIEH M. An imperialist competitive algorithm to schedule of receiving and shipping trucks in cross-docking systems[J]. The International Journal of Advanced Manufacturing Technology， 2010， 51（9/10/11/12）： 1179-1193.

[11] 孟洪潮. 多策略改進的混合帝国竞争算法[J]. 价值工程， 2018， 37（14）： 193-195. （MENG H C. Improved imperialist competitive algorithm based on quantum behavior[J]. Value Engineering， 2018， 37（14）： 193-195.）

[12] CHANG P， HUANG W， WU J， et al. A block mining and re-combination enhanced genetic algorithm for the permutation flowshop scheduling problem[J]. International Journal of Production Economics， 2013， 141（1）： 45-55.

[13] CHEN M H， CHEN S H， CHANG P C. Imperial competitive algorithm with policy learning for the traveling salesman problem[J]. Soft Computing， 2017， 12（7）： 1863-1875.

[14] HUANG W H， CHANG P C， WANG L C， et al. A fast block-based evolutional algorithm for combinatorial problems[J]. International Journal of Computer， Electrical， Automation， Control and Information Engineering， 2012， 6（7）： 889-895.

[15] PASTI R， de CASTRO L N. A neuro-immune network for solving the traveling salesman problem[C]// Proceedings of the 2006 IEEE International Joint Conference on Neural Networks. Piscataway： IEEE， 2006： 3760-3766.

[16] SOMHOM S， MODARES A， ENKAWA T. A self-organizing model for the travelling salesman problem[J]. Journal of the Operational Research Society， 1997， 48（9）： 919-928.