强化最优和最差狼的郊狼优化算法及其二次指派问题应用
张新明 王豆豆 陈海燕 毛文涛 窦 智 刘尚旺

摘 要:针对郊狼优化算法(COA)优化性能不足的问题,提出一种强化最优和最差狼的COA(BWCOA)方法。首先,对于组内最差郊狼的成长,在最优郊狼引导的基础上引入全局最优郊狼引导操作,以提高最差郊狼的社会适应能力(局部搜索能力);然后,在组内最优郊狼的成长过程中嵌入一种随机扰动操作,即以郊狼之间的随机扰动促进成长,发挥组内每个郊狼的能动性,提高种群的多样性进而强化全局搜索能力;
最后,组内其他郊狼的成长方式保持不变。将BWCOA运用到复杂函数优化和以医院科室布局为例的二次指派问题(QAP)中。
在CEC-2014复杂函数上的实验结果表明,与COA以及其他最先进的算法相比,BWCOA获得1.63的平均均值排名和Friedman检验中1.68的秩均值,均排名第一。另外,在6组QAP上的实验结果表明,BWCOA获得了5次均值最优的结果。
实验结果均表明BWCOA具有更强的竞争性。
关键词: 智能优化算法;郊狼优化算法;全局最优;二次指派问题;医院科室定位
中图分类号:TP181
文献标志码:A
Abstract: In view of poor performance of Coyote Optimization Algorithm (COA), a Best and Worst coyotes strengthened COA (BWCOA) was proposed. Firstly, for growth of the worst coyote in the group, a global optimal coyote guiding operation was introduced on the basis of the optimal coyote guidance to improve the social adaptability (local search ability) of the worst coyote. Then, a random perturbation operation was embedded in the growth process of the optimal coyote in the group, which means using the random perturbation between coyotes to promote the development of the coyotes and make full play of the initiative of each coyotes in the group to improve the diversity of the population and thus to enhance the global search ability, while the growing pattern of the other coyotes kept unchanged. BWCOA was applied to complex function optimization and Quadratic Assignment Problem (QAP) using hospital department layout as an example. Experimental results on CEC-2014 complex functions show that compared with COA and other state-of-the-art algorithms, BWCOA obtains 1.63 in the average ranking and 1.68 rank mean in the Friedman test, both of the results are the best. Experimental results on 6 QAP benchmark sets show that BWCOA obtains the best mean values for 5 times. These prove that BWCOA is more competitive.Key words: intelligent optimization algorithm; Coyote Optimization Algorithm (COA); global optimal; Quadratic Assignment Problem (QAP); hospital department location
0 引言
現实生活中随处存在着优化问题,以往人们依靠生活经验和数学分析的方法来求得最优解。但随着科学技术的发展,需要解决的优化问题越来越复杂,越来越多样,传统的方法不能很好解决这些问题[1]。因此,许多受某些自然现象和生物信息启发的智能优化算法被提出,如粒子群优化(Particle Swarm Optimization, PSO)算法[2]、人工免疫算法(Artificial Immune Algorithm, AIA)[1]、生物地理学优化(Biogeography-Based Optimization, BBO)算法[3]、灰狼优化(Grey Wolf Optimizer, GWO)算法[4]、蛙跳算法(Shuffled Frog Leading Algorithm, SFLA)[5]和萤火虫算法(Firefly Algorithm, FA)[6]。这些算法易于实现,能较好地解决各种复杂的优化问题,受到广大学者的关注。但是“无免费午餐定理”[4]表明某个算法不可能解决所有的问题,因此,新算法和改进的算法不断地产生来解决复杂优化问题。
二次指派问题(Quadratic Assignment Problem, QAP)是一个复杂的优化问题,在不同的领域中有广泛的应用,比如医院科室布局问题[7]、求解物流设施[8]、任务分配问题和航班调度问题等[9]。用智能优化算法来解决QAP也是热点之一,比如使用混合分布估计算法求解物流设施QAP,利用水循环优化算法求解QAP,提出混合搜索算法解决QAP等[8]。
受分布在北美的犬种的灵感,2018年Pierezan等[10]提出了郊狼优化算法(Coyote Optimization Algorithm, COA),模拟郊狼群生活、成长、生死、被组驱离和接纳等现象。在COA中,每一头郊狼代表一个候选解,每个解向量由郊狼的社会状态因子构成,这些状态因子包括郊狼内在因素和外在因素,每一个状态因素代表一个决策变量,用社会适应能力来衡量一头郊狼的好坏。
虽然COA与GWO都是狼群优化算法,但COA的不同之处在于:GWO根据动物的等级和狩猎方式来进行搜索,而COA关注狼的社会结构和文化背景;GWO中使用三头等级较高的灰狼来引导其他的灰狼捕猎,而COA中仅仅使用一头最好的狼来引导郊狼成长。
COA与SFLA在结构上比较相似,都是把一个种群分成几组子群来进行迭代,但SFLA的子群中只对最差的青蛙进行更新,而COA对子群中的每一头郊狼实施成长过程。
COA是一种新颖的智能优化算法,有着独特的搜索模型和框架,有较好的开采能力和探索能力。但由于COA提出时间短,仍有许多地方需要完善以及拓展应用领域。
因此,本文提出了一种强化最优和最差狼的COA(Best and Worst coyotes strengthened COA, BWCOA)來增强COA的优化性能。
在COA的基础上,对于组内最差郊狼成长,引入全局最优郊狼引导操作,提高局部搜索能力。对于组内最优郊狼成长,嵌入一种随机扰动操作,提高种群的多样性进而强化全局搜索能力。如此形成BWCOA。
另外,将COA的贪心算法替换为静态贪心算法,以提高算法的稳定性和增强全局搜索能力;并将种群分组参数设置为动态调整提高可操作性。
整个迭代完成之后,选择最能适应环境的郊狼作为问题的全局解决方案。从算法1可以看出,COA有以下优点:1)COA把郊狼群随机分为多个子狼群,有较好的搜索模型和框架,与PSO等算法相比,具有更好的探索能力;2)通过alpha狼和cult对郊狼的成长引导,COA具有较强的开采能力;3)通过出生死亡和环境因素影响的变异操作,COA具有较强的探索能力;4)COA对组内每个解进行更新,与SFLA相比,有更高的获得最优解的概率;5)随机分组,并在每次演化中,子组随机选择驱离和接受郊狼,使得种群多样性增强;6)采用贪心算法(步骤7))获得成长后的郊狼又参与随后郊狼的成长过程,可以加速收敛,这种贪心算法称为动态贪心算法。
2 强化最优和最差狼的郊狼优化算法
2.1 COA存在的问题及改进的动机
虽然COA有许多优点,但由于提出时间短,仍有许多地方需要完善,如在处理某些复杂优化问题时,优化性能不足。从算法1可以看出,在组内郊狼成长中,依靠组内最优郊狼的引导,可能会导致算法陷入局部最优。郊狼的出生和死亡操作虽有一定的全局搜索能力,但在处理一些复杂优化问题时,探索能力不足。另外,依据行政管理学的“抓两头带中间”的思想,即在一个单位人员管理中,抓好先进和后进就可以带动中间人员的积极性,以便提高整个单位人员的工作效率。因此,为了提高郊狼算法的优化性能,本文提出了一种强化最优和最差狼的COA(BWCOA)。
2.2 全局最优郊狼引导强化最差郊狼
在COA中,每组郊狼生长是根据组内的最优郊狼和组文化趋势以及两头随机郊狼来更新的,局部搜索能力受限。本文在最差郊狼在组内成长过程中,嵌入了一种全局最优郊狼引导操作。如式(10)和(11)所示:
其中:rand(1,D)是D维的随机变量;Cg是全局最优郊狼;Cl是组内最优郊狼;Cw是组内最差的郊狼。选择对最差郊狼进行全局最优郊狼的引导,可以保证最差的郊狼向着最优位置趋近,提高算法的局部搜索能力。
另外,为了保证算法在开采和探索之间保持平衡,在搜索的前期,采用式(10)进行组内最差郊狼成长操作,从式(10)可以看出,在全局最优郊狼、组内最优郊狼和组内最差郊狼的差值的基础上乘以系数(2*rand(1,D)-1),其范围为-1到1,且每一维都在随机扰动,在组内最差郊狼的每一状态因子周围大范围的搜索,以此在提高算法局部搜索能力的同时兼顾全局搜索能力。在搜索的后期,更注重局部开采,使用式(11)来进行组内最差郊狼成长操作。从式(11)可以看出,在全局最优郊狼、组内最优郊狼和组内最差郊狼的差值的基础上乘以系数(0.5+0.5*rand),其范围为0.5到1,且此系数对于每一维都是一样的,在组内最差郊狼的周围小范围地搜索,更强化算法的局部搜索能力。
2.3 随机扰动强化最优郊狼
在COA中,郊狼的生死算子能获得全局搜索能力,从算法1可以看出,组内郊狼成长算子能获得局部搜索能力,但是每一次迭代,组内郊狼成长执行Np*Nc次,而郊狼的生死只执行Np次。全局搜索能力与局部搜索能力不能很好地保持平衡。而依据现代智能理论,一个优化算法只有在全局搜索能力与局部搜索能力达到平衡时,才能获得最佳的优化性能。因此,为了提高全局搜索能力,在子群的最优郊狼成长过程中嵌入一种随机扰动操作见式(12):
其中:a和b是在种群中随机选择的两头郊狼的标号。从式(12)可以看出,组内最优郊狼受两部分的影响:第一部分是组内最差郊狼;第二部分是全局最优郊狼和最差郊狼的差值加上两个随机郊狼的差值。全局最优郊狼和组内最差郊狼的区别较大,两者相减范围较大,再加上两个随机选择的郊狼差值,使得郊狼的成长过程不仅受到全局最优郊狼的影响,而且也受子群中郊狼的相互影响,增加了种群的多样性,进而提高全局搜索能力。
3.4 收敛性分析
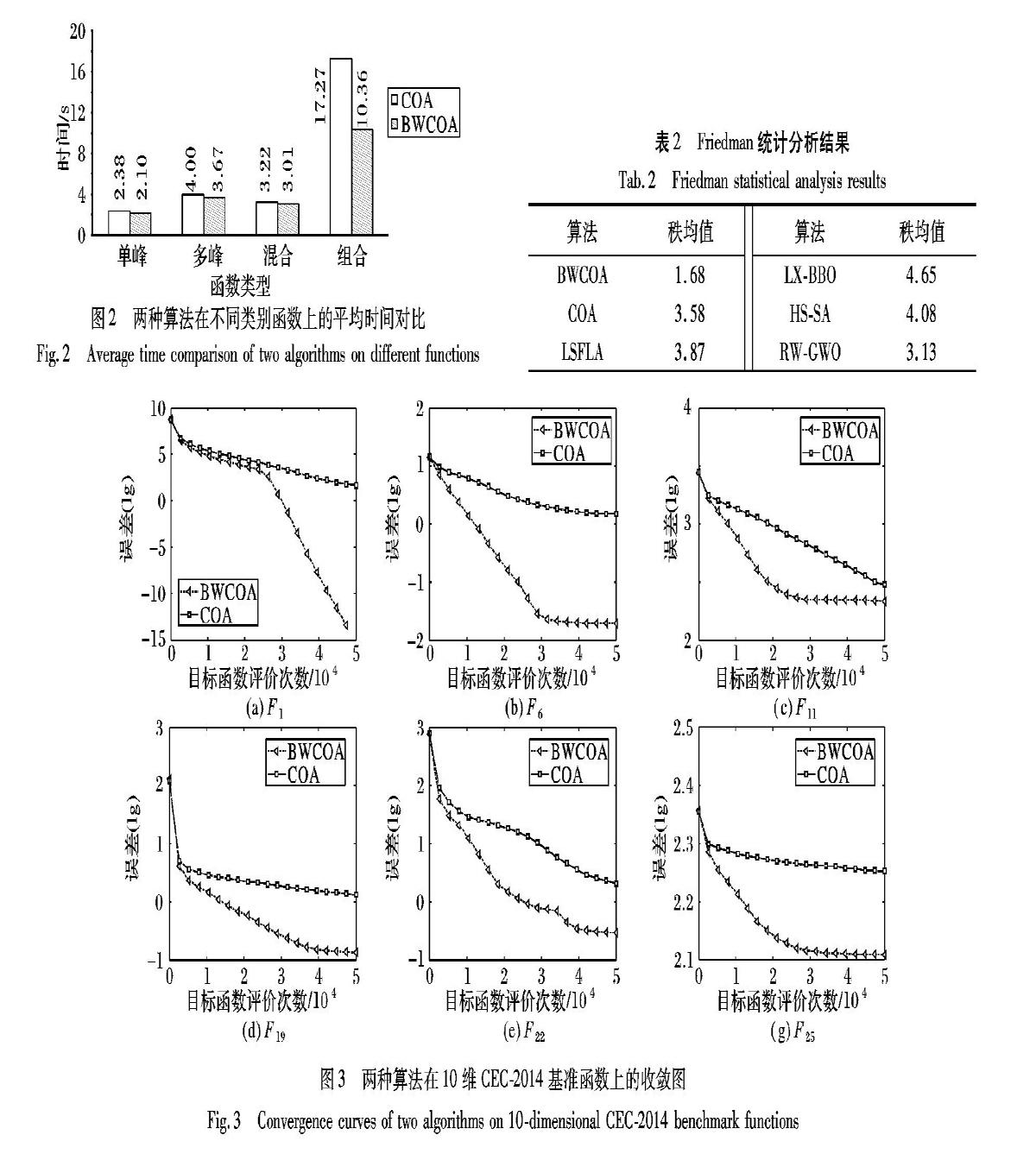
本文是对COA的改进算法,因此,本节只对BWCOA和COA进行收敛性分析。两种算法在CEC-2014基准函数上做实验,公共参数如下:D=10,MaxNFs为10000*D,Run为51,N为40。选取部分函数做收敛性分析,选取的函数与3.1节相同。代表性函数的收敛如图3所示。
从图3可以看出,在6个函数上,BWCOA的收敛速度都明显优于COA的收敛速度。在单峰函数(图3(a))上,BWCOA的收敛速度大幅度地优于COA的收敛速度,特别是在迭代25000次之后,表明BWCOA提高了算法的开采能力和寻优精度;在多峰函数(图3(b)、(c)),BWCOA的收敛速度都比COA的收敛速度快,特别是在迭代5000次之后,BWCOA的收敛速度大幅度地优于COA,表明BWCOA提高了探索能力,很好地平衡探索与开采;在混合函数(图3(e)和组合函数(图3(f))上,BWCOA的收敛速度比COA的收敛速度快,特别是在迭代2000次之后,BWCOA的收敛速度大幅度地优于COA,表明BWCOA在处理复杂优化函数时,表现优异。因此,BWCOA提高了COA的收敛速度。
3.5 在二次指派问题上的应用
QAP是多项式时间内不可解的组合优化问题,最早由Koopmans和Beckmann在1957年提出[17],QAP可以描述为将一组设施分配给一组位置的问题,这些位置之间有给定的距离,且设施之间有给定的流。求解QAP是根据任意两个位置之间的距离和任意两个设备之间的流,将一组设备分配到一组位置的问题,以最小化成本见式(13)。
常用两个矩阵来表示设施(F)和位置(L),每个矩阵的大小为T*T。 fxy是每对设施之间的流或权重,代表从设施x到设施y的流或权重。dxy表示位置x到位置y的距离。
QAP可以应用到许多实际的问题上,例如,医院科室定位的建模,以优化科室的配置,减少每个病人的时间消耗,提高医院为病人服务的效率。例如一个简单的例子,在一间医院的某单层,
在某单层中,每个科室的重要程度不一样,人流多的科室比较重要;相反,人流少的科室次重要,两个科室之间的重要度由流表示。矩阵F代表两个部门之间的流,矩阵L代表两个位置之间的距离。下一步是将这组科室分配到这组地点,使患者在科室之间的成本最小化。
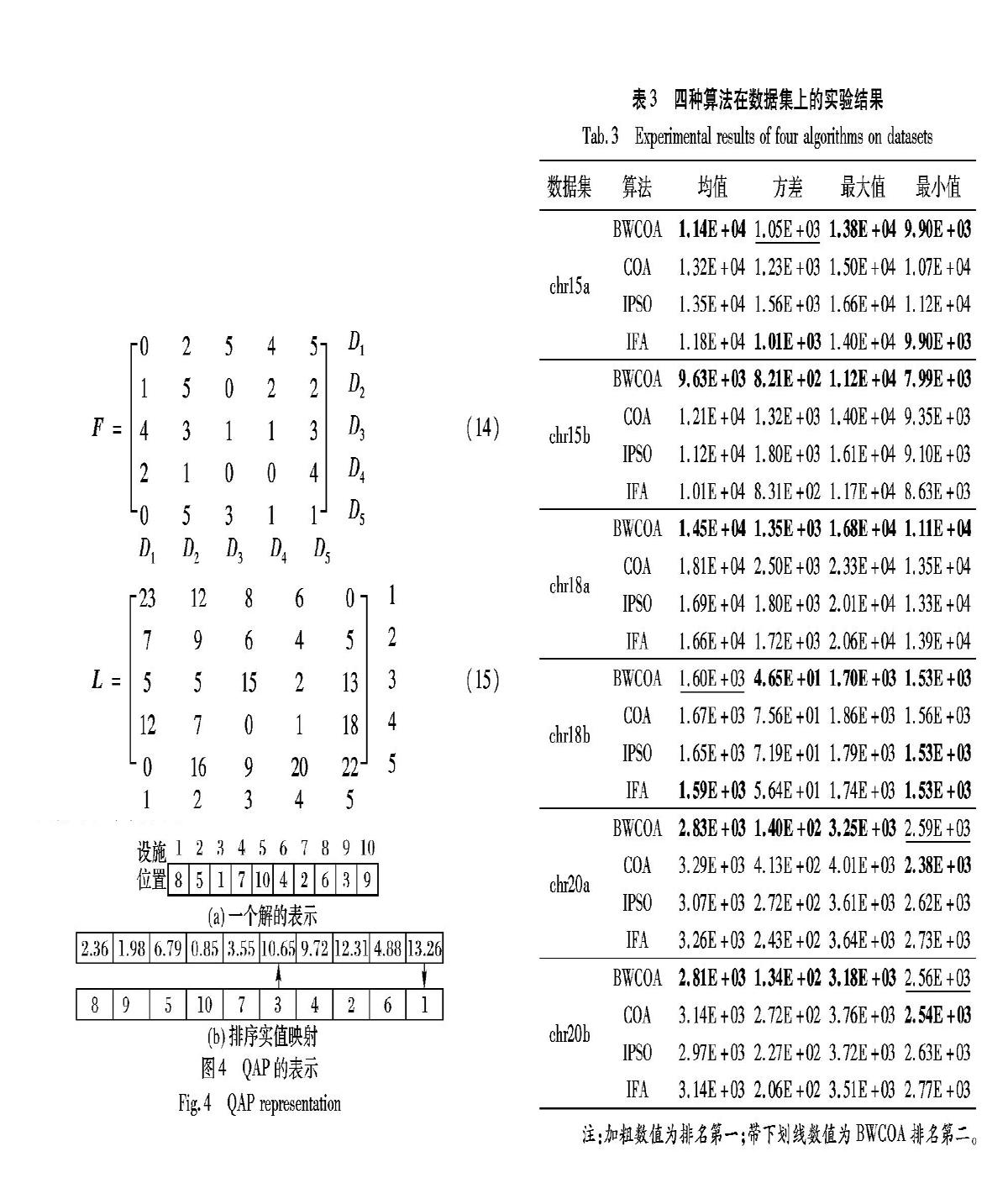
使用BWCOA解决QAP,首先应解决如何将用于连续优化问题的BWCOA用于离散优化问题。本文借鉴文献[7]的方法,每个解的维数代表QAP中位置或者设施的数量,每个解代表不同位置的排列,对应一种位置分配方案,通过算法循环迭代,找到最优的分配方案。假设一个QAP,有10个设施点,需要分配到10个位置点,如图4(a)所示。1号设施分配到8号位置,2号设施分配到5号位置,3号设施分配到1号位置,等等。QAP被认为是一个排列离散问题,因此当智能优化算法解决QAP时,使用最大实值将实值映射成排列序列,如图4(b)所示。
本文用BWCOA来解决QAP,对比算法采用COA、IPSO(Improved PSO)和IFA(Improved Firefly Algorithm)。IPSO和IFA来自网站(http://yarpiz.com/359/ ypap104-quadratic-assignment-problem),是PSO和FA的改进算法,擅长解决QAP,因此,具有较强的可比性。
4种算法的参数设置如下:N是100,Run为30,最大迭代次数是1000。实验记录了每个算法在数据集上的均值、方差、最大值和最小值。在表3中,基准数据来自文献[7],一直作为解决QAP的标准集。
从表3可以看出:在数据集chr15a的方差、chrl8b的均值、chr20a的最小值和chr20b的最小值上,BWCOA排第二,其他的均排第一。总的来说, BWCOA能较好地处理QAP。
4 結语
COA是最近提出的一种智能优化算法,需要改进完善和扩展应用领域,因此,本文针对COA优化性能不佳,提出了一种改进的COA,即强化最优和最差狼的COA(BWCOA),并应用于QAP。首先,为了提高收敛速度,对于最差郊狼,在组内最优郊狼引导的基础上,嵌入全局最优郊狼引导操作。其次,为了进一步弥补全局搜索能力不足,对于组内的最优郊狼,在其成长过程中嵌入一种随机扰动操作,即以郊狼的相互作用影响成长过程,增强种群的多样性。最后,组内其他郊狼仍采用原成长方式不变,并采用静态贪心算法。CEC-2014基准函数的实验结果表明,与COA和其他对比算法相比,在总体上,BWCOA的优化性能优于对比算法。QAP的实验结果也表明与对比算法相比,BWCOA有更强的竞争性。在未来,将进一步完善COA,提高优化性能,并扩展其应用领域。
参考文献(References)
[1] SAVSANI P, JHALA R L, SAVSANI V. Effect of hybridizing Biogeography-Based Optimization (BBO) technique with Artificial Immune Algorithm (AIA) and Ant Colony Optimization (ACO) [J]. Applied Soft Computing, 2014, 21: 542-553.
[2] 张新明, 王霞, 涂强, 等. 融合榜样学习和反向学习的粒子群优化算法[J]. 河南师范大学学报(自然科学版), 2017, 45(6): 91-99. (ZHANG X M, WANG X, TU Q, et al. Particle swarm optimization algorithm combing example learning and opposition learning[J]. Journal of Henan Normal University (Natural Science Edition), 2017, 45(6): 91-99.)
[3] 張新明, 康强, 王霞, 等. 差分迁移和趋优变异的生物地理学优化算法[J]. 小型微型计算机系统, 2018, 39(6): 1168-1177. (ZHANG X M, KANG Q, WANG X, et al. Biogeography-based optimization with differential migration and global-best mutation[J]. Journal of Chinese Computer Systems, 2018, 39(6): 1168-1177.)
[4] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
[5] 陈暄, 徐见炜, 龙丹. 基于蚁群优化-蛙跳算法的云计算资源调度算法[J]. 计算机应用, 2018, 38(6): 1670-1674, 1681. (CHEN X, XU J W, LONG D. Resource scheduling algorithm of cloud computing based on ant colony optimization-shuffled frog leading algorithm[J]. Journal of Computer Applications, 2018, 38(6): 1670-1674, 1681.)
[6] AYDILEK I B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems[J]. Applied Soft Computing, 2018, 66: 232-249.
[7] ABDEL-BASSET M, MANOGARAN G, EL-SHAHAT D, et al. Integrating the whale algorithm with Tabu search for quadratic assignment problem: a new approach for locating hospital departments[J]. Applied Soft Computing, 2018, 73: 530-546.
[8] 戢守峰, 罗蓉娟, 孙琦, 等. 一种求解物流设施二次分配问题的混合分布估计算法[J]. 运筹与管理, 2018, 27(1): 74-83. (JI S F, LUO R J, SUN Q, et al. A hybrid estimation of distribution algorithm for quadratic assignment problem[J]. Operations Research and Management Science, 2018, 27(1): 74-83.)
[9] 牟廉明, 戴锡笠, 李坤, 等. 求解二次指派问题的最优迭代最大最小蚂蚁算法[J]. 计算机应用, 2014, 34(1): 199-203. (MOU L M, DAI X L, LI K, et al. Optimal iterative max-min ant system for solving quadratic assignment problem[J]. Journal of Computer Applications, 2014, 34(1): 199-203.)
[10] PIEREZAN J, COELHO L D S. Coyote optimization algorithm: a new metaheuristic for global optimization problems[C]// Proceedings of the 2018 IEEE Congress on Evolutionary Computation. Piscataway: IEEE, 2018: 1-8.
[11] LIANG J J, QU B Y, SUGANTHAN P N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization[EB/OL]. [2018-12-10]. http://bee22.com/manual/tf_images/Liang%20CEC2014.pdf.
[12] TANG D, YANG J, DONG S, et al. A levy flight-based shuffled frog-leaping algorithm and its applications for continuous optimization problems[J]. Applied Soft Computing, 2016, 49: 641-662.
[13] GARG V, DEEP K. Performance of Laplacian biogeography-based optimization algorithm on CEC 2014 continuous optimization benchmarks and camera calibration problem[J]. Swarm and Evolutionary Computation, 2016, 27: 132-144.
[14] ASSAD A, DEEP K. A hybrid harmony search and simulated annealing algorithm for continuous optimization[J]. Information Sciences, 2018, 450: 246-266.
[15] GUPTA S, DEEP K. A novel random walk grey wolf optimizer[J]. Swarm and Evolutionary Computation, 2019, 44: 101-112.
[16] 王艳娇, 史新梦. 跳跃海豚群算法[J/OL]. 控制理论与应用 [2019-03-05]. http://www.doc88.com/p-0087875377721.html. (WANG Y J, SHI X M. Jumping dolphin swarm algorithm[J]. Control Theory and Applications [2019-03-05]. http://www.doc88.com/p-0087875377721.html.)
[17] KOOPMANS T C, BECKMANN M J. Assignment problems and the location of economic activities[J]. Econometrica, 1957, 25(1): 53-76.
This work is partially supported by the National Natural Science Foundation of China (U1704158), the Key Research Project of Higher Education Institutions in Henan Province (19A520026).

