基于多目标蝗虫优化算法的移动机器人路径规划
黄超 梁圣涛 张毅 张杰

摘 要:在静态多障碍物环境下的移动机器人路径规划问题中,粒子群算法存在容易产生早熟收敛和局部寻优能力较差等缺点,导致机器人路径规划精度低。为此,提出一种多目标蝗虫优化算法(MOGOA)来解决这一问题。根据移动机器人路径规划要求将路径长度、平滑度和安全性作为路径优化的目标,建立相应的多目标优化问题的数学模型。在种群的搜索过程中,引入曲线自适应策略以提高算法收敛速度,并使用Pareto最优准则来解决三个目标之间的共存问题。实验结果表明:所提出的算法在解决上述问题中寻找到的路径更短,表现出更好的收敛性。该算法与多目标粒子群(MOPSO)算法相比路径长度减少了约2.01%,搜索到最小路径的迭代次数减少了约19.34%。
关键词:路径规划;移动机器人;蝗虫优化算法;多目标
中图分类号:TP242.6;TP23
文献标志码:A
Abstract: In the mobile robot path planning problem in static multi-obstacle environment, Particle Swarm Optimization (PSO) algorithm has the disadvantages of easy premature convergence and poor local optimization ability, resulting in low accuracy of robot path planning. To solve the problem, a Multi-Objective Grasshopper Optimization Algorithm (MOGOA) was proposed. The path length, smoothness and security were taken as path optimization targets according to the mobile robot path planning requirements, and the corresponding mathematical model of multi-objective optimization problem was established. In the process of population search, the curve adaptive strategy was introduced to speed up the convergence of the algorithm, and the Pareto optimal criterion was used to solve the coexistence problem of the above three targets. Experimental results show that the proposed algorithm finds shorter paths and shows better convergence while solving the above problems. Compared with the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm, the proposed algorithm has the path length reduced by about 2.01 percentage, and the number of iterations reduced by about 19.34 percentage.
Key words: path planning; mobile robot; grasshopper optimization algorithm; multi-objective
0 引言
在移动机器人导航系统中,规划一条最优路径成为近年来一个重要的课题,引起了众多研究者的关注[1]。移动机器人的最优路径规划问题,就是依据某些优化准则(工作代价最小如行走路线最短等),在其工作空间中找到一条从起始状态到目标状态并且能避开障碍物的最优路径。
当前在移动机器人路径规划中常用的粒子群(Particle Swarm Optimization, PSO)算法[2]属于进化算法的一种,与模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解,利用适应度来评价解的品质,并通过追随当前搜索到的最优值来寻找全局最优。该算法的优点是实现容易、精度高、收敛快;但容易产生早熟收敛,局部寻优能力较差。贾会群等[3]为了提高路径规划的精度,对基本粒子群算法进行改进,将各阶段惯性因子和加速因子使用三角函数方式进行自适应调节,并且引入了鸡群算法中的母鸡更新方程和小鸡更新方程,提高了算法的搜索能力。多目标进化算法结合粒子群算法的研究在国内外已经取得了研究成果,2018年杨景明等[4]将帕累托(Pareto)解集与“多点变异”引入粒子群算法中,避免了算法陷入早熟收敛。但是多目标粒子群(Multi-Objective PSO, MOPSO)算法在解集分布性、收敛性方面仍然存在不足。
近年来,一些学者提出了元启发式方法[5]来克服经典方法的不足。特别是在大范围和高自由度问题中,蝗虫优化算法(Grasshopper Optimisation Algorithm, GOA)[6]由Saremi等于2017年1月提出。蝗虫算法相较于粒子群算法[7]具有良好的全局搜索能力和收敛速度。因为该算法的提出时间较短,目前对该算法的研究文献较少,现在主要是对算法的应用场景和算法自身的改进两个方面。2017年,Tumuluru等[8]利用蝗虫优化算法更新癌症分级问题中神经网络的权值;2017年,Barman等[9]将蝗虫优化算法应用于电力负荷预测问题中的向量机参数估计问题中。在算法改进的方面,2017年Mirjalili等[10]提出了一种多目标蝗虫优化算法(Multi-Objective Grasshopper Optimization Algorithm, MOGOA);2018年閆旭等[11]将量子旋转门引入基本蝗虫优化算法,并应用到车间调度问题;2017年,程泽新等[12]首次将蝗虫算法应用到解决无人机(Unmanned Aerial Vehicle, UAV)三维航迹规划问题中,并能够规划出一条较优路径。但由于UAV所处的环境障碍物较少、环境简单,将蝗虫优化算法引入移动机器人路径规划当中,其所处的环境相较于空中环境要复杂,所以容易陷入局部最优和收敛精度不足。本文提出应用曲线调整策略自适应更新c参数来平衡局部搜索能力和全局搜索能力,提高算法的搜索能力;然后引入多目标最优方法来获得合适的导航路线;最终提高了算法的收敛性及稳定性。
为了平衡种群搜索和开发,需要用c参数动态调整蝗虫群的勘探和开发,同时应减小与迭代次数成比例的舒适区,采用曲线自适应更新策略刚好弥补这一不足。式(15)中采用的是余弦自适应方式,余弦函数在开始和结束时下降速率小,余弦自适应调整参数c在前期的值比式(16)线性调整的值大,增加蝗虫的搜索能力,随着迭代次数的增加,搜索的效率提高,蝗虫群会朝目标位置附近收敛;后期c参数的比式(16)中的小,可以缩小蝗虫的搜索范围,增加蝗虫的局部搜索能力。这些特点使得在不陷入局部最优的情况下,极大地提高了算法的收敛速度。
2)添加外部储存archive集来保存搜索过程中的非支配解。每次迭代过程对支配解集B进行位置更新,并对更新后的支配解集B与archive中的粒子进行比较,若xi∈B,且xj∈archive,使得xi支配xj,则删除xj,使xi加入A更新外部archive,全局最优解从外部储存archive中选出。具有最短和最光滑路径约束的多目标路径规划优化模型的主要目标是获得多目标Pareto最优解,因此,根据决策空间可行解集λ和Pareto最优解F(p*),
MOGOA的主要目的是确定通过确定保存在archive中的Pareto最优解集X的支配关系,
若新的候选解优于当前解,则优胜劣汰,不断更新当前解和全局最优解解。
2.2.2 算法流程
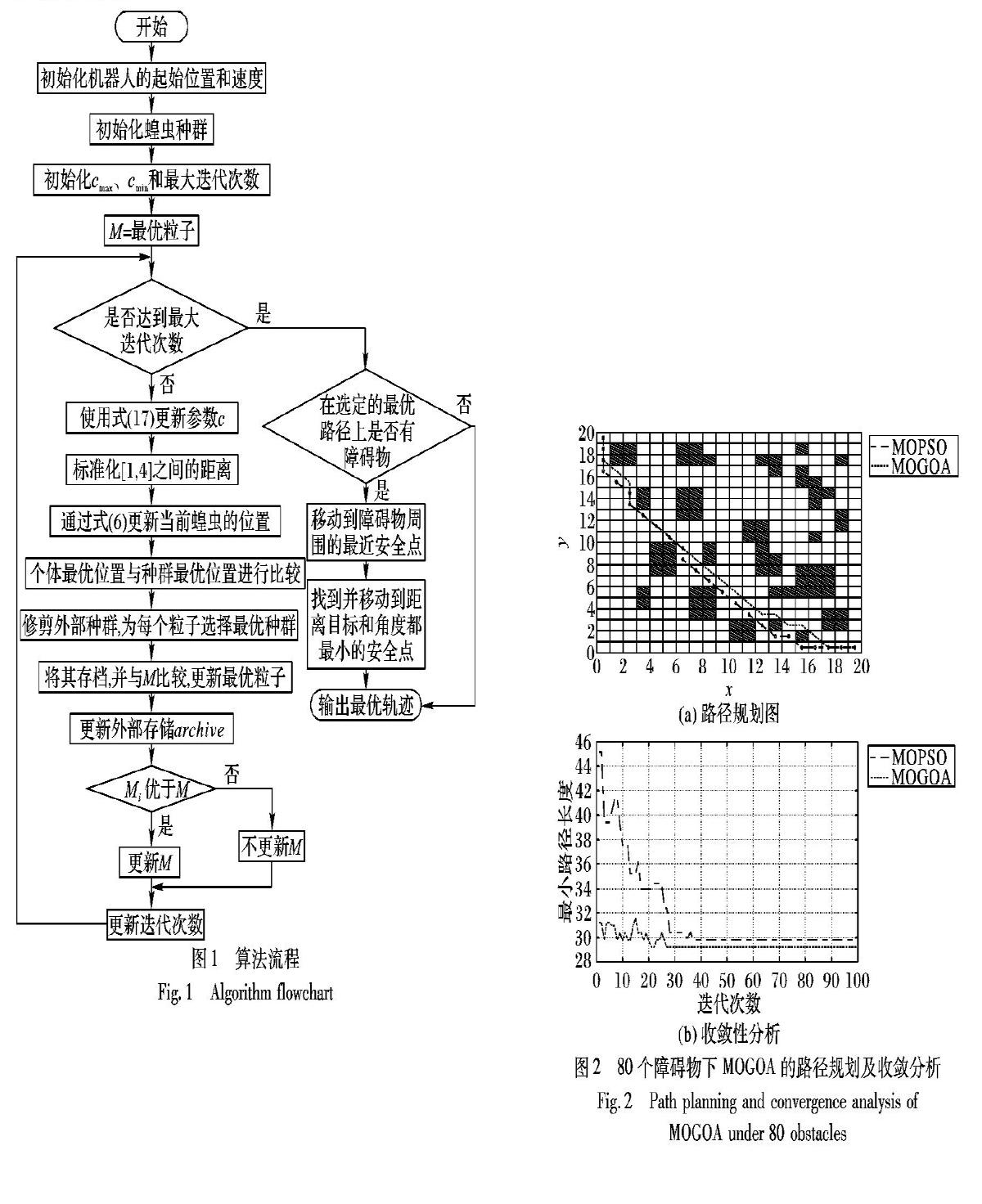
算法流程见图1,具体算法步骤如下:
1)初始化蝗虫种群的初始位置、種群规模及算法中的各参数,如:cmax、cmin、最大迭代次数;
2)计算蝗虫群每个搜索个体的适应度值,并找出当前全局最优解;
3)M=最优粒子;
4)使用式(17)更新参数c;
5)标准化区间在[1,4]的蝗虫之间的距离;
6)通过式(6)更新当前粒子的位置;
7)修剪外部种群,为每个粒子选择全局最优位置;
8)计算并选择每个粒子的个体历史最优位置和种群最优位置进行比较;
9)将每个粒子的最优位置粒子存档,与M进行比较,更新最优粒子;
10)根据新的非支配解与已存档的非支配解的比较,更新外部存储archive;
11)移动机器人绕开障碍物,选择距离目标最安全的点,输出最优轨迹。
2.2.3 评价指标该算法在多个障碍物且数目不同的环境中进行了性能和效率的测试。
第一个测试标准是最优解错误率(Error Ratio, ER)[16],本文使用一个标准来评估多目标优化算法的性能,测量解是否为实际Pareto最优解的概率,ER是评价帕累托最优解算法精度的一个很好指标。计算方法如下:
其中:m为Pareto最优解的个数。当xi=0时,得到的解是Pareto最优解;否则,xi=1。
第二个测试标注是最优解覆盖率SCM(Set Coverage Metric)[17],计算公式如下:
其中:A和B是目标空间中的两个非支配解,即覆盖率是B中的非支配解被A中非支配解覆盖的个数在B中所占比例[18];|B|表示集合B中元素的个数;表示Pareto占优。
由式(19)可知,SCM(A,B)∈[0,1]。SCM(A,B)值越大,表示解集A覆盖解集B的程度越高,也就是说A优于B的程度也越高,当SCM(A,B)>SCM(B,A)时,表示解集A覆盖解集B的比例要小于解集B覆盖解集A的比例,说明解集A中的非支配解要优于解集B中的非支配解集。
3 实验与结果分析
仿真实验所用软件是Matlab R2014,在具有Intel i7处理器(2.8 GHz)CPU和16 GB RAM的联想笔记本上实现。最大迭代次数为100,cmax=1,cmin=0.00001。MOPSO的参数组合为:c1=c2=1.5,权重系数为0.8,最大最小权重系数分别为0.2和0.9。在环境1和环境2中,蝗群规模和粒子群规模均设置为500。
为了验证该算法相较于粒子群算法的优越性,与文献[19]中的多目标粒子群(MOPSO)算法进行比较。实验环境均采用20×20方格,初始位置的坐标为(0,20),目标位置的位置为(20,0),黑色阴影部分表示环境中的障碍物。
在环境1中,将障碍物的数量设置为80,图2是MOGOA与MOPSO在80个障碍物数目下的路径规划结果和收敛性分析。
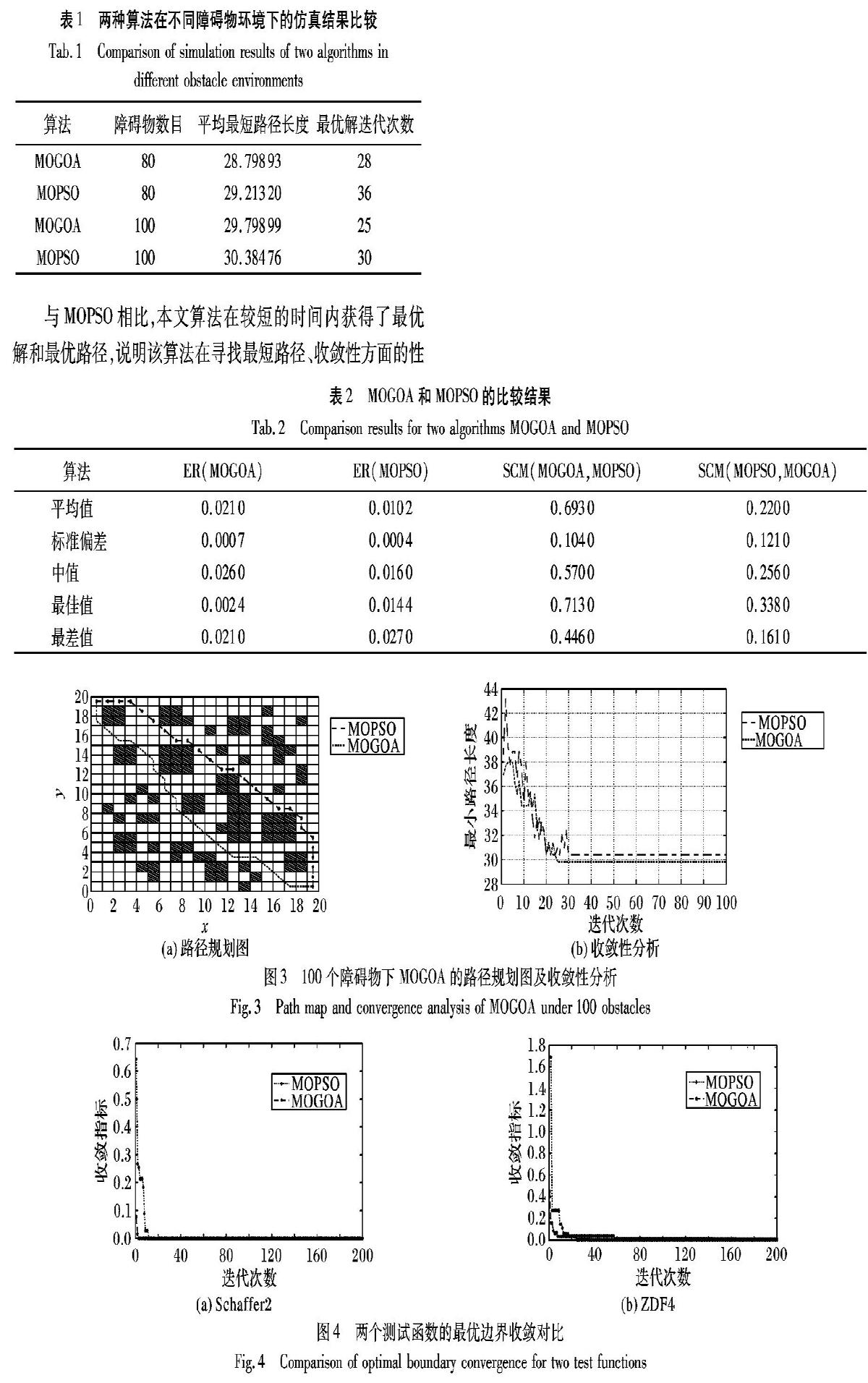
在环境2中,将障碍物的数量增加为100。图3是MOGOA与MOPSO在100个障碍物数目下的路径规划结果和收敛性分析。
在环境1和环境2不同的障碍物数目下得到的路径长度和迭代次数进行比较分析。从表1可看出,不论在环境1还是环境2中,MOGOA在路径长度均小于MOPSO,且收敛速度较快。多目标蝗虫群算法(MOGOA)与多目标粒子群(MOPSO)算法相比路径长度缩短了约2.01%,搜索到最小路径的迭代次数相比减少了约19.34%。本文算法提高了蝗虫优化算法的搜索能力,同时也提高了算法的收敛速度。
表2为MOGOA和MOPSO在ER和SCM两个指标的运算结果,为通过算法10次独立运行后获得。从表2可以明显看出,MOGOA的解集错误率都明显低于MOPSO,同时在解集覆盖度SCM(MOGOA,MOPSO)也都大于SCM(MOPSO,MOGOA),表明MOGOA在Pareto最优解精度方面优于MOPSO。因此,实验结果表明,MOGOA能很好地收敛于帕累托最优解。与MOPSO相比,本文算法在较短的时间内获得了最优解和最优路径,说明该算法在寻找最短路径、收敛性方面的性能优于PSO算法。
为了验证MOGOA的性能,将MOPSO和MOGOA在Schaffer2和ZDF4两个多目标测试函数上进行对比,它们的最优边界收敛对比结果如图4所示。Schaffer2和ZDF4具有不同的复杂度情况:Schaffer是一个一维两个极小值点的函数;ZDT4是一个多维多个极小值点的函数。
[11] 閆旭, 叶春明.混合蝗虫优化算法求解作业车间调度问题[J]. 计算机工程与应用, 2019, 55(6): 257-264. (YAN X, YE C M. Hybrid grasshopper optimization algorithm solves job-shop scheduling problem [J]. Computer Engineering and Applications 2019, 55(6): 257-264.)
[12] 程泽新, 李东生, 高杨.基于蝗虫算法的无人机三维航迹规划[J]. 飞行力学, 2019, 37(2): 46-50, 55. (CHENG Z X, LI D S, GAO Y. UAV three-dimensional path planning based on grasshopper algorithm[J]. Flight Dynamics, 2019, 37(2): 46-50, 55.)
[13] HUA Y, JIN Y, HAO K. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts[J]. IEEE Transactions on Cybernetics, 2019, 49(7): 2758-2770.
[14] THABIT S, MOHADES A. Multi-robot path planning based on multi-objective particle swarm optimization[J]. IEEE Access, 2018, 7: 2138-2147.
[15] MAC T T, COPOT C, TRAN D T, et al. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization[J]. Applied Soft Computing, 2017, 59: 68-76.
[16] COELLO C A C, LAMONT G B, van VELDHUIZEN D A. Evolutionary algorithms for solving multi-objective problems[M]. Boston: Springer, 2002.
[17] SHIM M, SUH M, FURUKAWA T, et al. Pareto-based continuous evolutionary algorithms for multiobjective optimization[J]. Engineering Computations, 2002, 19(1): 22-48.
[18] FENG W, ZHANG L, YANG S, et al. A multiobjective evolutionary algorithm based on coordinate transformation[J]. IEEE Transactions on Cybernetics, 2019, 49(7): 2732-2743.
[19] DI L, ZHENG Z, XIA M. Robot path planning based on an improved multi-objective PSO method[C]// Proceedings of the 2016 International Conferenceon Computer Engineering, Information Science & Application Technology. Paris: Atlantis Press, 2016: 496-501.

