无梁楼盖结构不同计算方法分析比较
牛 寅,郝 济,李振清
(1.国家建筑工程质量监督检验中心,北京 100013;2.北京市住房城乡建设委员会,北京 101100;3.鄂尔多斯市建设工程质量监督站,内蒙古 鄂尔多斯 017000)
0 引 言
无梁楼盖结构是在柱、内墙、外墙上直接支撑楼板,柱间不设置框架梁或仅在楼板内设置暗梁,通过配筋的不同在楼板内区分柱上板带和跨中板带,为满足抗冲切要求,板、柱连接处一般设置有柱帽,柱帽可采用矩形柱帽或斜柱帽,荷载通过楼板直接传递至柱或墙体。无梁楼盖体系不需要设置框架梁,在满足建筑净高要求的前提下可有效减少结构层高、减少地下车库开挖深度、便于顶板通风喷淋等系统设备的布置,降低建设成本。
1 受力特点及结构计算模型建立
在无梁楼盖承载力分析时,可将楼板简化为支承在柱上的等代梁,再根据支承及约束情况的不同将等代梁划分为柱上板带和跨中板带进行受力分析。结构计算时,将柱两侧相邻楼板 1/4 跨度之和定义为柱上板带,将柱上板带范围外的楼板定义为跨中板带。内力分析时,按划分的板带及柱组成多跨连续梁进行计算。
2 常用计算方法
无梁楼盖结构计算常用的方法有等代平面框架法、经验系数法和有限元法。
其中经验系数法、等代平面框架法是将空间无梁楼盖结构体系简化为多跨连续梁进行求解。按经验系数法计算时,应先算出楼板受所有垂直分布荷载产生的板的总弯矩设计值然后按照弯矩分配系数确定柱上板带和跨中板带跨中及支座处的弯矩设计值;等代框架法是将柱、墙体、楼板等代梁组成平面等代框架后,分别计算平面等代框架在竖向荷载和水平荷载下的内力。
有限元分析方法是通过有限元计算软件将无梁楼盖结构进行网格划分后,由有限元软件进行求解。近年来,随着有限元计算软件的不断发展与完善,有限元法在无梁楼盖的计算中应用越来越广泛。目前国内常用的有限元计算软件有中国建筑科学研究院有限公司PKPM 系列软件和北京某公司的盈建科结构计算软件。这两款结构计算软件中,都针对无梁楼盖结构体系设置了专门的计算模块,结构计算时,先建立整体结构模型,在无梁楼盖计算模块中输入柱帽并完成板带划分,模型建立后由软件进行网格划分及计算分析。
3 工程实例
河北省廊坊市某住宅小区地下车库,建筑面积2 万 m2,采用无梁楼盖结构体系。车库柱网尺寸端跨6.0 m×8.1 m、内跨 8.1 m×8.1 m,层高 4.0 m,车库顶板厚度为 450 mm,柱帽尺寸 2.5 m×2.5 m×0.45 m,混凝土设计强度等级为 C 35,钢筋强度等级为 HRB 400 级,车库顶覆土厚度 1.0 m。基于工程实例,分别采用经验系数法、等代框架法、PKPM 中的楼板计算软件分别进行模型建立和内力分析,并将计算结果进行比对。
根据 GB 50009-2012《建筑结构荷载规范》钢筋混凝土容重取 25kN/m3,板底吊挂荷载重取 0.4 kN/m3,覆土容重取 20 kN/m3,活荷载按板顶有消防车通过取值 20 kN/m2,荷载组合设计值:q=1.2×q恒+1.4q活=65.98 kN/m2,结构几何尺寸如图1 所示,标准荷载如图2 所示。
3.1 经验系数法计算结果
按经验系数法计算时应先算出所有垂直分布荷载产生的板的总弯矩设计值,然后按确定柱上板带和跨中板带的弯矩设计值M0(Mx=(1/8)qby(lx-(2/3)C)2、My=(1/8)qbx(ly-(2/3)C)2)[1](注:公式中 C-柱帽在弯矩方向的有效宽度,无柱帽时取 0)。求得跨中弯矩设计值M0后,即可将此弯矩按一定比例分配为柱上板带的支座弯矩和跨中弯矩以及跨中板带的支座弯矩和跨中弯矩四部分,板带弯矩值如表1 所示,根据经验系数法的分配系数求得各部位弯矩结果如表2 所示。
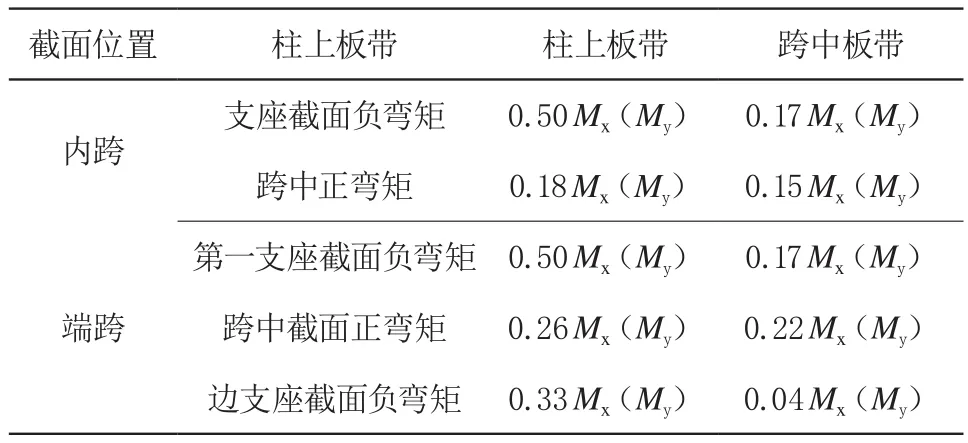
表1 经验系数法板带弯矩值
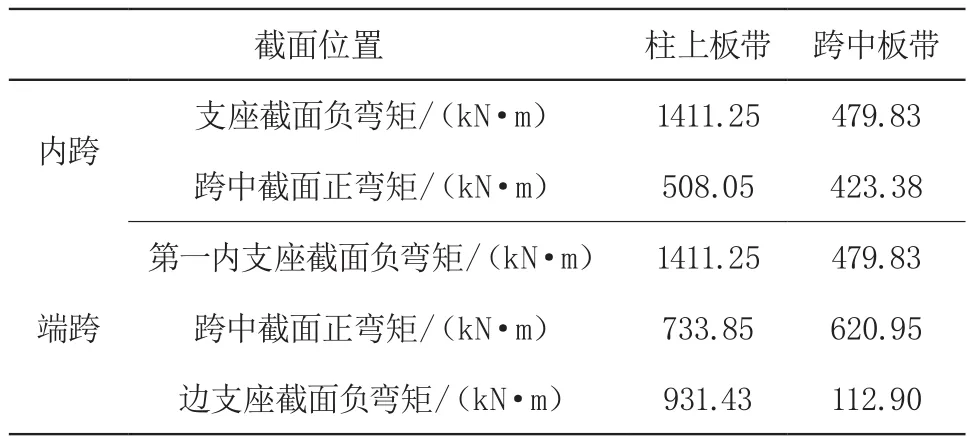
表2 经验系数法计算结果
3.2 等代框架法计算结果
等代框架法是以支柱为中心,取一定宽度的楼板当做“等代梁”,组成等代框架,然后在两个方向分别计算平面框架。计算采用理正工具箱 TBS5.7 版中无梁楼盖等代框架模块进行,计算弯矩如图3 所示,计算得到的各部位弯矩结果如表3 所示。

图1 结构几何尺寸简图(单位:mm)
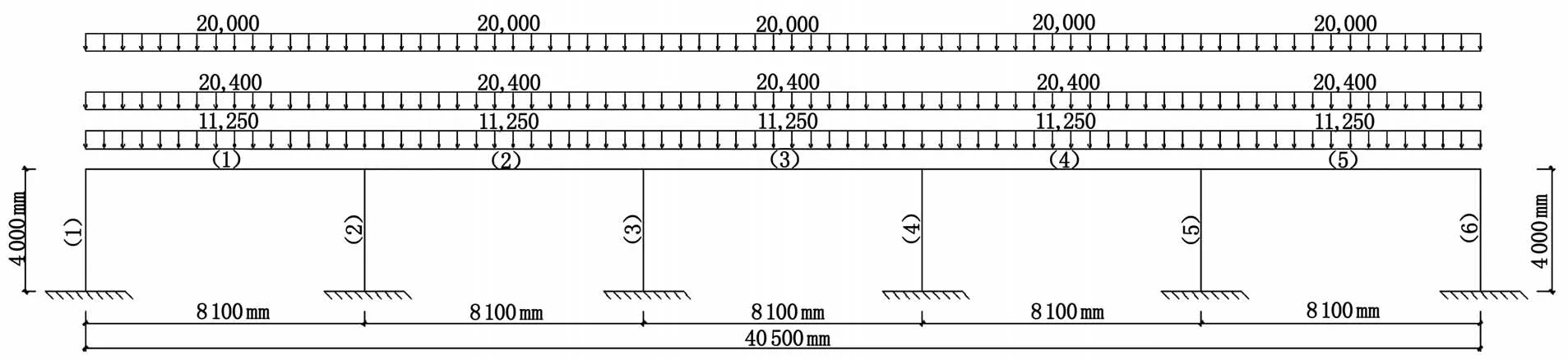
图2 荷载标准值简图(单位:kN/m2)

图3 等代框架弯矩计算结果
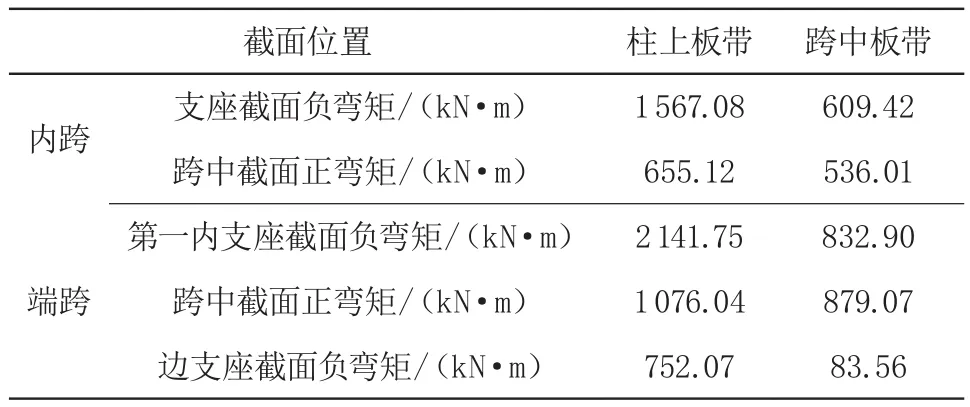
表3 等代框架法计算结果
3.3 有限元法计算结果
采用中国建筑科学研究院有限公司 PKPM(V3.1.5)系列中的楼板计算软件对无梁楼盖结构进行建模验算。有限元法计算分析结果如表4 所示。
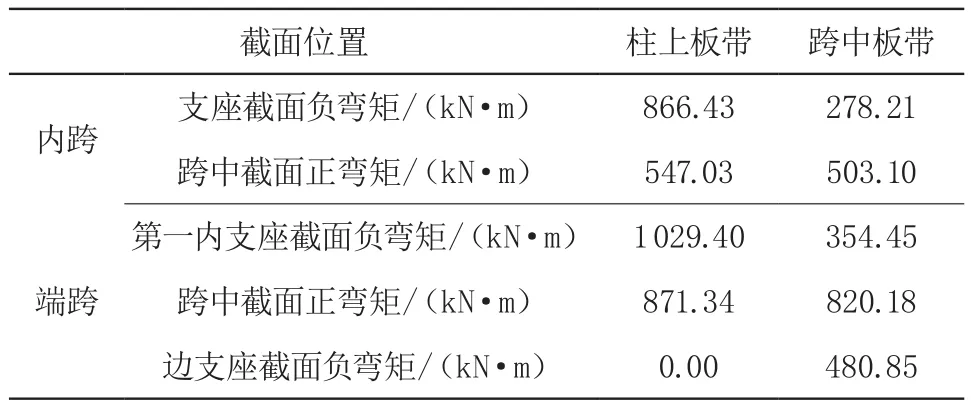
表4 有限元法计算分析结果
3.4 计算结果对比分析
3 种方法计算所得弯矩结果比较如表5 所示,有限元法计算所得弯矩云图如图4、图5 所示。3 种计算方法计算所得内跨柱上板带、跨中板带的跨中截面正弯矩均相差不大,其中等代框架法计算所得跨中截面正弯矩最大,与经验系数法计算结果相比大 29 %;3 种计算方法所得内跨支座截面负弯矩、端跨计算弯矩均存在明显差异,这与计算中是否考虑外墙对内力分布影响有关,其中等代框架法计算中考虑了结构外墙对内力的影响,计算模型相对经验系数法更合理。

表5 计算分析结果比较

图4 板顶弯矩云图
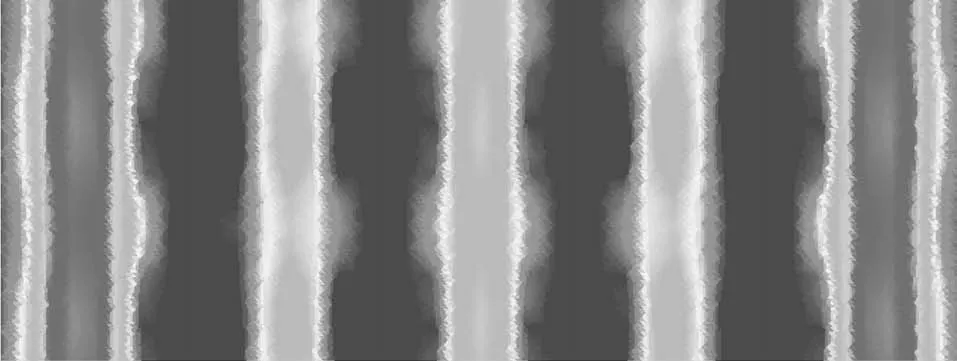
图5 板底弯矩云图
有限元法计算时,将结果划分为细小的单元,各单元之间变形协调,有限元法计算真实地反映了楼板的实际受力过程,计算结果更接近于实际内力分布情况,通过观察有限元法计算弯矩云图,无梁楼盖受力按照板带分布特征明显[2]。
4 结 语
通过对不同方法计算结果的分析,由于等代框架法和经验系数法计算模型的不同,引起计算所得设计弯矩产生区别,从而对无梁楼盖构件截面选择和钢筋配置产生影响,因两种方法计算模型的特点,这两种方法仅适用于建筑规模不大、结构布置相对规则的建筑,实际工程中,推荐使用结构模型相对合理的等代框架法进行简单的结构计算。然而近年来实际工程案例中,无梁楼盖常用于地下车库的结构设计中,地下车库结构存在建筑规模大、地库上部荷载情况复杂、结构布置不规则等特点,在这种情况下,有限元软件通过精细的网格划分,对柱帽、支座处内力计算更准确,极大地提高了复杂柱网下无梁楼盖结构计算的精度与效率,具有明显优势,有限元法将是无梁楼盖结构计算方法的发展方向。

