薄壁与厚壁管材力学性能的统一评价方法—广义缺口环法
聂光临,包亦望,万德田
薄壁与厚壁管材力学性能的统一评价方法—广义缺口环法
聂光临,包亦望,万德田
(中国建筑材料科学研究总院有限公司,绿色建筑材料国家重点实验室,北京 100024)
管材作为一类重要的材料制品结构形式,其力学性能的准确测试对于保障管材构件服役安全性与可靠性至关重要。目前所提出的缺口环法为测试管材力学性能提供了可行方案,但缺口环法测试管材弹性模量与弯曲强度的计算公式仅适用于薄壁管材。为实现厚壁管材力学性能的准确测试,本研究将径向力与切向力对管材试样的变形能考虑在内,基于曲杆分析理论,提出了适用范围更广的广义缺口环法。以三点弯曲法测得的石英玻璃梁试样弹性模量(72.08±1.87 GPa)与弯曲强度(73.84±6.67 MPa)作为参比,分别利用缺口环法与广义缺口环法测得了同一批次石英玻璃管材试样的弹性模量与弯曲强度,测试结果表明:随着管材壁厚的增加,缺口环法测试结果与广义缺口环法测试结果的相对偏差逐渐增大;且广义缺口环法测得的石英玻璃弹性模量和弯曲强度值与三点弯曲法的测试结果更接近,即广义缺口环法的测试结果更准确;同时表明了广义缺口环法既适用于薄壁管材的力学性能测试,也适用于厚壁管材的力学性能测试。
管材;弹性模量;弯曲强度;缺口环法;广义缺口环法
0 引言
陶瓷、玻璃、水泥基材料制成的各类管/环状构件在工程中得到广泛应用,例如:氧化铝陶瓷耐磨管、石英玻璃管液位计、混凝土给排水管道等。这些管材制品在服役期间均会承受外载作用,因此其力学性能的准确可靠性评价对于管材构件的选材、安全设计、寿命预测等至关重要。弹性模量与弯曲强度作为重要的力学性能参数,可衡量材料抵抗弹性变形的能力与确定构件的承载极限,是保障构件安全服役的前提,因此管材力学性能的准确测试评价直接关系到管材构件的安全可靠性和对破坏的预测性。
目前广泛使用的管/环状材料力学性能测试方法——缺口环法仅适用于薄壁管材(内半径与外半径之比/>9/11)[1,2],因为缺口环法测试管材弹性模量的计算公式在推导过程中,忽略了径向力与切向力对缺口环试样在压缩过程中变形能的影响,即按照直梁的计算方法推导了缺口环法测试弹性模量的计算公式。然而,常使用的管材不仅包括薄壁管材,而且厚壁管材也占据了一定比 例[3,4],且通常为了提高管材的承载能力、抗渗性及服役寿命,也需要加大管材构件的壁厚。对于这类厚壁管材弹性模量的测试评价,可将其减薄后,再按照缺口环法测试其弹性模量;但是管/环状异形构件的加工较为困难,因此管材壁厚减薄存在一定的操作困难。因此,针对厚壁管材弹性模量的准确测试评价尚处于研究空白,需要提出一种适用于厚壁管材弹性模量测试的方法。为填补这一研究空白,本文基于曲杆分析理论提出了广义缺口环法,其适用范围更广,既适用于薄壁管材的力学性能测试,也适用于厚壁管材的力学性能测试。
1 基本原理
1.1 缺口环法
缺口环法是指通过对一个缺口环试样施加径向压缩载荷,根据其弹性范围内的载荷—位移曲线斜率及试样的几何尺寸测试其弹性模量的方 法[5, 6]。对于薄壁管材(/>9/11),其弯曲正应力可近似地用直梁公式(纯弯曲)计算,属于小曲率曲 杆[7],可按照直梁分析法对缺口环法测量管材力学性能的计算公式进行推导,可由下式计算得缺口环试样的弹性模量与弯曲强度[1, 2]。
式中,为弹性模量(MPa);为缺口环试样的轴向长度(mm);为缺口环试样的外半径(mm);为缺口环试样的内半径(mm);Δ为线弹性范围内的载荷增量(N);Δ为Δ作用下所产生的压缩变形量(mm);max为弯曲强度(MPa);为弯矩(N·mm);max为拉应力最大位置处到中性轴的间距(mm),max=(-)/2;为试样横截面惯性矩(mm4),=(-)3/12;max为缺口环试样开裂破坏的临界载荷值(N);A为试样横截面的面积(mm2)。
1.2 广义缺口环法
为实现厚壁管材力学性能的准确测试,本研究将径向力与切向力对缺口环试样的压缩变形能的影响考虑在内,基于曲杆分析法推导得管材弹性模量与弯曲强度的计算公式,称为广义缺口环法。缺口环试样在压缩载荷作用下,其受力分析如图1所示,其内力可由下式计算。
缺口环试样在压缩过程中的变形能除弯曲变形能外,还包括径向力和切向力的变形能,其计算式如下:

式中,为变形能;为试样横截面对中性轴的静矩;为剪切模量;为与横截面形状有关的系数,在矩形截面的情况下,值可取1.2[7]。根据卡氏定理[8]可得:
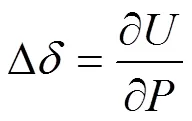

式(6)为利用曲杆分析理论推导得的缺口环法测试弹性模量的计算公式,与文献[1]、[2]、[9]中弹性模量计算式不同,因为文献[1]、[2]、[9]中弹性模量测试方法只适用于/>9/11的薄壁管材(弹性模量计算公式的推导过程中忽略了径向力与切向力对缺口环试样变形能的影响)。
采用Ansys 15.0有限元模拟分析软件,选择Solid Quad 8 node 183单元类型,在缺口环试样上端节点处施加压缩载荷,下端节点施加约束,模拟缺口环试样的实际受力状态,得到其应力分布如图2所示。缺口环试样的外侧受拉,而内侧受压,且1/2高度处圆环外侧所受拉应力最大,因此在压缩载荷作用下,裂纹会首先萌生于1/2高度处圆环外侧,而后向圆环内侧迅速扩展。

图2 有限元模拟分析缺口环试样的应力分布图
由材料力学[7]分析可得横截面上各点的正应力为:
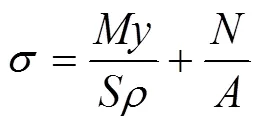

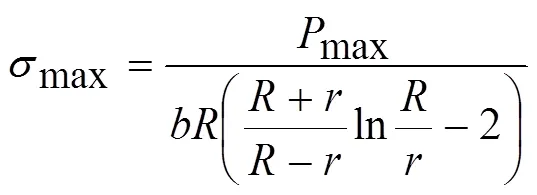
式中,max为缺口环试样裂纹萌生处所受的最大拉应力,即为试样的弯曲强度。上式(8)与国际标准ISO 18558:2015(E)[10]中弯曲强度计算式一致,即ISO 18558中弯曲强度计算式是基于曲杆分析计算得来的。
2 实验
为研究缺口环法与广义缺口环法测量管材弹性模量与弯曲强度的适用范围,实验选用不同壁厚的石英玻璃管,几何尺寸如表1所示。/变化范围为0.65~0.90,随着/比值的降低,石英玻璃管壁厚逐渐增大。
表1 石英玻璃管试样的几何尺寸

Tab.1 Geometric dimensions of the quartz glass tubes
另外,取同一生产批次的石英玻璃,将其切割加工成3 mm×20 mm×120 mm板状试样,参照JC/T 676-1997《玻璃材料弯曲强度试验方法》[11],利用三点弯曲法测试其弯曲强度,三点弯曲试验下跨距选用100 mm,加载速率2 mm/min。注意:在弯曲强度测试过程中,为避免强度的时间效应,必须控制加载速率,使得试样发生开裂破坏的时间均在30 s左右。同时参照GB/T 10700-2006《精细陶瓷弹性模量试验方法弯曲法》[12],利用三点弯曲试验测试石英玻璃的弹性模量,下跨距选用100 mm,加载速率0.5 mm/min,载荷上限选用30 N。
缺口环法测试不同壁厚的石英玻璃管试样时,应调整加载速率使得弹性模量测试时间(加载至载荷上限所需时间)为60 s左右,载荷上限值应小于其断裂载荷值的1/2;且在弯曲强度试验中,应尽量控制试样在30 s左右发生开裂破坏,以避免时间效应对强度测试值的影响。在弹性模量测试过程中,应调整试验机采样频率为100~200 Hz,以确保试验机所记录的载荷—横梁位移曲线的完整性;在弯曲强度测试过程中,仅当开裂破坏位置位于缺口环试样的1/2高度时,才可认为所测得的开裂临界载荷值是有效的。
3 结果与讨论
3.1 弹性模量
石英玻璃缺口环试样在压缩载荷作用下直至发生开裂破坏,其载荷—横梁位移曲线如图3所示,随着/的减小,即随着缺口环试样壁厚逐渐增大,试样的断裂临界载荷值逐渐增大,而其压缩变形量却在逐渐减小。对于/=0.90的石英玻璃缺口环试样,其在2~10 N内的压缩变形量约为200 μm;对于/=0.65的石英玻璃缺 口环试样,其在10~190 N内的压缩变形量约为75 μm。对于石英玻璃试样而言,缺口环试样(/=0.65~0.90)的压缩变形量较大(>70 μm),采用电感量仪可以准确测得其变形,继而可得其弹性模量值。
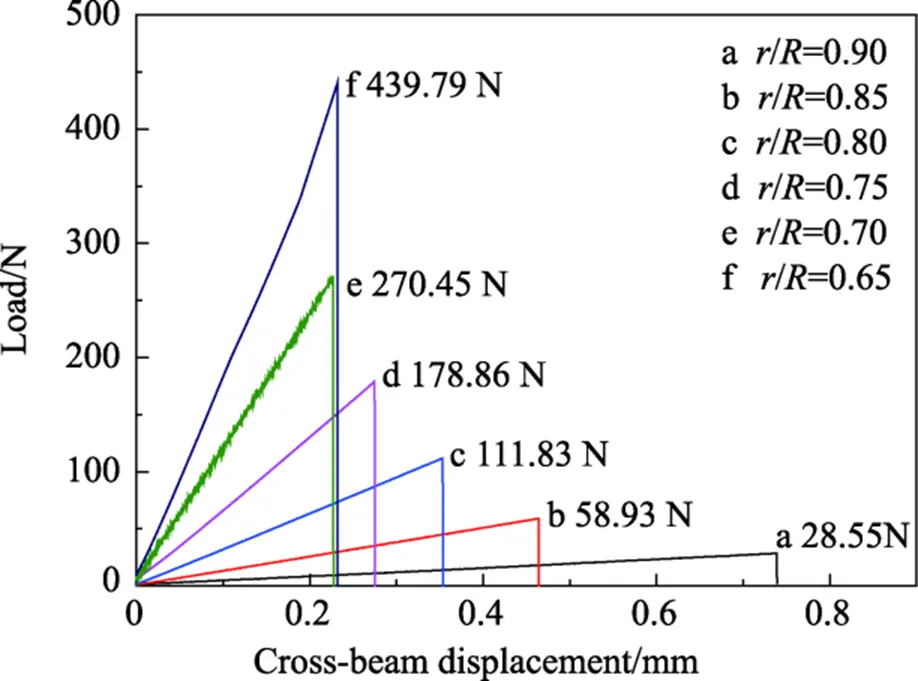
图3 不同壁厚石英玻璃缺口环试样的载荷—横梁位移曲线
参照GB/T 10700-2006《精细陶瓷弹性模量试验方法弯曲法》[12],利用三点弯曲试验测得石英玻璃的弹性模量为72.08±1.87 GPa。利用缺口环法与广义缺口环法的计算公式(式1与式6),分别测得了不同壁厚的石英玻璃缺口环试样的弹性模量,并将测试结果与三点弯曲法测得的弹性模量值作比较,测试结果如表2所示。
随着/逐渐减小,缺口环试样的壁厚逐渐增大,广义缺口环法测得的弹性模量值与缺口环法测试值的偏差逐渐增大,二者最大偏差仅为1.57%。/在0.90~0.65变化范围内,考虑径向力与切向力(广义缺口环法)测得的弹性模量值(式6)与不考虑径向力与切向力(缺口环法)测得的弹性模量值(式1)相近,且两种计算方法测得的管材弹性模量值与三点弯曲法测得的弹性模量基本一致(/=0.65时,与三点弯曲法测试值的最大偏差为-2.85%)。总的来说,在/=0.90~0.65的范围内,广义缺口环法测得的管材弹性模量值更接近三点弯曲法的测试结果,即广义缺口环法测试管材弹性模量的准确性更高。
由于试验未制得/<0.65的缺口环试样,因此缺乏广义缺口环法与缺口环法测试/<0.65的厚壁管材弹性模量值之间比较的数据。可采用将相同外半径、相同轴向长度、相同力学响应参数(Δ/Δ)、不同内半径(即不同/)代入式(6)与式(1),可得/=0.60、0.55、0.50时,广义缺口环法测试模量值1与缺口环法测试值2间的相对偏差分别为6.74%、14.14%、23.42%。则对于缺口环法测试弹性模量,在/>0.55的范围内,径向力与切向力对管材弹性模量测试值的影响较小(<10%);而当/≤0.55时,径向力与切向力对管材弹性模量测试值的影响较大,此时应按照广义缺口环法测试厚壁管材的弹性模量。
表2 缺口环压缩试验测试弹性模量的试验结果

Tab.2 Test results of the elastic modulus measured by split ring compressing experiments
注:1为基于广义缺口环法测得的弹性模量值;2为基于缺口环法测得的弹性模量值;3为三点弯曲法测得的弹性模量值,3=72.08±1.87 GPa。
3.2 弯曲强度
参照行业标准JC/T 676-1997《玻璃材料弯曲强度试验方法》[11],利用三点弯曲试验测得石英玻璃的弯曲强度为73.84±6.67 MPa,将此测试结果作为参考,以验证广义缺口环法测试不同壁厚石英玻璃管材弯曲强度的准确性。利用缺口环压缩试验测试石英玻璃管的弯曲强度时,缺口环试样断裂破坏后形貌如图4所示,缺口环试样的有效破坏形式应是在管材试样1/2高度处发生断裂破坏,且为典型的突发性脆性断裂。

图4 石英玻璃缺口环试样照片:(a)断裂前;(b)断裂后
利用广义缺口环法与缺口环法的计算公式(式8与式2),分别测得了不同壁厚的石英玻璃缺口环试样弯曲强度,并将测试结果与三点弯曲测得的弯曲强度作比较,测试结果如表3所示。
随着/逐渐减小至0.65,石英玻璃缺口环试样的壁厚逐渐增大,广义缺口环法(式8)测得的弯曲强度值与缺口环法(式2)测试值的偏差逐渐增大;且当/≤0.75时,二者相对偏差较大(>10%),二者最大偏差为-15.76% (/=0.65时)。/在0.90~0.65变化范围内,考虑径向力与切向力(广义缺口环法)测得的弯曲强度值与三点弯曲法测试值基本相近,二者最大偏差仅为-5.02%。/在0.90~0.70变化范围内,不考虑径向力与切向力(缺口环法)测得的弯曲强度值与三点弯曲法测试值基本相近,二者最大偏差仅为6.50%;而当/=0.65时,缺口环法测得的弯曲强度值与三点弯曲法测试值相差较大(13.12%)。由此可知,在/=0.90~0.65的范围内,广义缺口环法测得的弯曲强度值更接近三点弯曲法的测试结果,即广义缺口环法测试管材弯曲强度的准确性更高。
4 结论
针对厚壁管材力学性能的测试技术难题,本研究将径向力与切向力对缺口环试样变形能的影响考虑在内,基于曲杆分析理论提出了广义缺口环法,旨在提高管材力学性能的测试准确性。
1) 对于缺口环压缩试验测试弹性模量,在/>0.55的范围内,径向力与切向力对管材弹性模量测试值的影响较小,/=0.60时,广义缺口环法测试值与缺口环法测试值相差6.74%;而当/≤0.55,须利用广义缺口环法(式6)测试管材弹性模量,其测试值与三点弯曲法测试结果更相近,即将径向力与切向力考虑在内测得的弹性模量更加准确。
2) 对于缺口环压缩试验测试弯曲强度,在/>0.75的范围内,径向力与切向力对管材弹性模量测试值的影响较小,/=0.80时,广义缺口环法测得的弯曲强度值与缺口环法的测试结果仅相差-7.82%;而当/≤0.75时,广义缺口环法测试管材弯曲强度更准确,必须利用广义缺口环法(式8,考虑径向力与切向力的影响)测试缺口环试样的弯曲强度。
表3 缺口环压缩试验测试弹性模量的试验结果
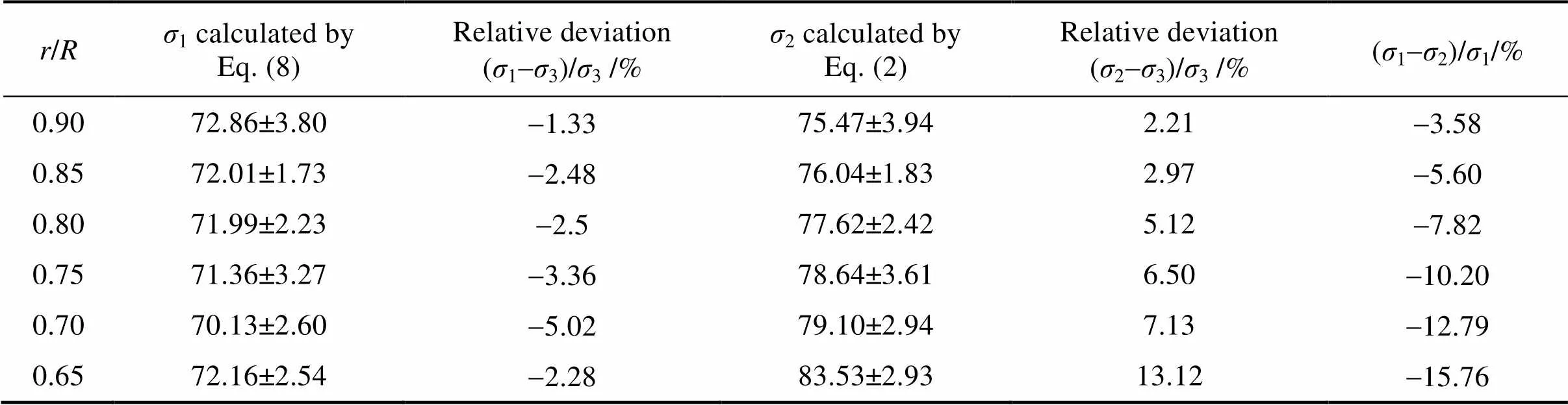
Tab.3 Test results of the elastic modulus measured by split ring compressing experiments
注:1为基于广义缺口环法测得的弯曲强度值;2为基于缺口环法测得的弯曲强度值;3为三点弯曲法测得的弯曲强度值,3=73.84±6.67 MPa。
综上所述,由于广义缺口环法计算公式推导过程中考虑了径向力与切向力的影响(更接近于缺口环试样的实际受力情况),其适用范围较原有缺口环法更广,适用于薄壁与厚壁管材力学性能(弹性模量与弯曲强度)的统一评价。
[1] WAN D T, BAO Y W, LIU X G, et al. Evaluation of elastic modulus and strength of glass and brittle ceramic materials by compressing a notched ring specimen [J]. Advanced Materials Research, 2011, 177: 114-117.
[2] 包亦望, 万德田, 刘正权, 等.一种评价圆环或圆管状脆性材料弹性模量和强度的方法 [P]. 中国专利: ZL 201010544550.1, 2013-02-20.
[3] KIM N H, OH C S, KIM Y J, et al. Limit loads and fracture mechanics parameters for thick-walled pipes [J]. International Journal of Pressure Vessels and Piping, 2011, 88: 403-414.
[4] JUSZKIEWICZ G, NOWAK T. Comparative study on thin and thick walled cylinder models subjected to thermo-mechanical loading [J]. Composite Structures, 2015, 134: 142-146.
[5] 包亦望, 聂光临, 万德田. 相对法及特殊条件下陶瓷材料力学性能评价[J]. 硅酸盐学报, 2017, 45(08): 18-29. BAO Y W, NIE G L, WAN D T. Journal of the Chinese Ceramic Society, 2017, 45(08): 18-29.
[6] 包亦望, 万德田. 结构陶瓷特殊条件下力学性能评价的新技术与技巧[J]. 科学通报, 2015, 60(3): 246-256. BAO Y W, WAN D T. Chinese Science Bulletin, 2015, 60(3): 246-256.
[7] 刘鸿文. 材料力学第三版下册[M]. 北京: 高等教育出版社, 1992: 183-204.
[8] BEER F P, JOHNSTON E R, DEWOLF J T, et al. Mechanics of Materials [M]. Sixth ed. America: McGraw– Hill, 2012: 734-744.
[9] LIU Z, BAO Y W, WAN D T, et al. A novel method to evaluate Young's modulus of ceramics at high temperature up to 2100 °C [J]. Ceramics International, 2015, 41: 12835-12840.
[10] ISO 18558:2015(E), Fine ceramics (advanced ceramics, advanced technical ceramics) — Test method for determining elastic modulus and bending strength of ceramic tube and rings [S]. Switzerland: International Organization for Standardization, 2015.
[11] JC/T 676-1997, 玻璃材料弯曲强度试验方法[S].
[12] GB/T 10700-2006, 精细陶瓷弹性模量试验方法弯曲法[S].
Unified Determination Method for Mechanical Properties of Thin-walled and Thick-walled Tubes — General Split Ring Method
NIE Guanglin, BAO Yiwang, WAN Detian
(State Key Laboratory of Green Building Materials, China Building Materials Academy Co., Ltd., Beijing 100024, China)
Tube is a kind of significant form of material product structure, and the accurate evaluation of the tube mechanical properties is crucially important for insuring the service safety and reliability of the tube components. The presented split ring method provides feasible solution to the determination of tube mechanical properties, but the formulas for calculating the elastic modulus and bending strength apply only to the thin-walled tubes. To determine the mechanical properties of thick-walled tubes accurately, the general split ring method with wider application range was proposed in this study based on the analytical theory for curved bar, by taking into account the effect of the radial and tangential forces on the strain energy of the tube sample. The three-point bending method was used to test the elastic modulus (72.08±1.87 GPa) and bending strength (73.84±6.67 MPa) of the quartz glass beams, and the test result can be used as the reference data. Both the split ring method and general split ring method were used to determine the elastic modulus and bending strength of the same quartz glass tubes. The test results indicate that the relative deviation between the measured data by split ring method and general split ring method gradually increased with the rising wall thickness of the tube samples. The elastic modulus and bending strength tested by the general split ring method were closer to the test results by three-point bending method, i.e., the results measured by the general split ring method were more accurate. And the general split ring method can be used to determine the mechanical properties for both the thin-walled and thick-walled tubes.
tube; elastic modulus; bending strength; split ring method; general split ring method
date: 2019‒03‒18.
date:2019‒04‒25.
国家自然科学基金(51472227);国家重点研发计划(2017YFB0310401)
Correspondent author:BAO Yiwang(1957-), male, Ph.D., Professor. E-mail:ywbao@ctc.ac.cn
TQ174.75
A
1000-2278(2019)04-0524-06
10.13957/j.cnki.tcxb.2019.04.019
2019‒03‒18。
2019‒04‒25。
包亦望(1957-),男,博士,教授。

