对高中数学试题评讲课的一点思考

☉江苏省南京市行知实验中学 徐 敏

考试完后，教师要做的第一件事就是评讲试卷，上试卷评讲课.如何上好试题评讲课，需要教师认真思考，积极探索.在日常教学中，我们不难发现，有的老师在讲评试题时，只公布答案，其结果必然是学生知其然而不知其所以然，以后遇到相类似的题目，他们依然是“一头雾水”或“重蹈覆辙”.其实任何一道精心设计的数学试题，都蕴含着丰富的数学思想，如果教师在评讲试题时注重思想方法的渗透、技能技巧的传授、解题误区的提醒等，那么学生会“吃一堑长一智”，从而养成良好的思维品格.所以说，讲评课也要讲究教法，只有正确的教法才能促使学生的思维得到进一步发展.那么数学评讲课应特别注意哪些细节问题呢？本文做了一点思考.

思考一、试卷评讲课要注重“一题多解”，培养学生思维的求异性

讲评时，教师可以启发学生从不同角度去思考问题，让学生展示多种解题思路，以提高学生的综合分析能力和数学知识的整合能力，发展他们的求异思维.在讲评试题时，教师不能仅仅满足于常规方法的介绍，更要引导学生探究一些既简单明了又凸显数学本质的，极富创造性的解题思路，这样才能使学生的思维水平有所提高，使数学能力“更上一层楼”.

案例1已知点A，B，C 满足5，则的值是______.

本题出自一次期中测试，难度中等，全班正确率达百分之八十二，可能有的教师认为这种题可让学生自己订正，不必在讲评课上大费周章，但笔者却认为，越是基础性的问题，讲评时越要讲到位，可谓“小题大做”，让学生从一个题目中感悟多种方法.于是，笔者引导学生发现了以下五种解题思路：

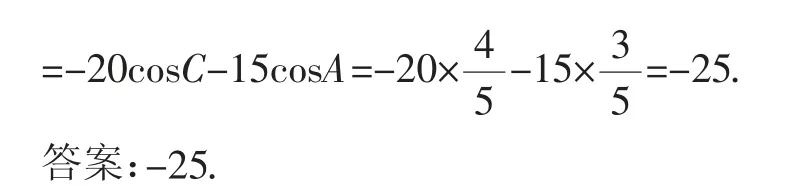
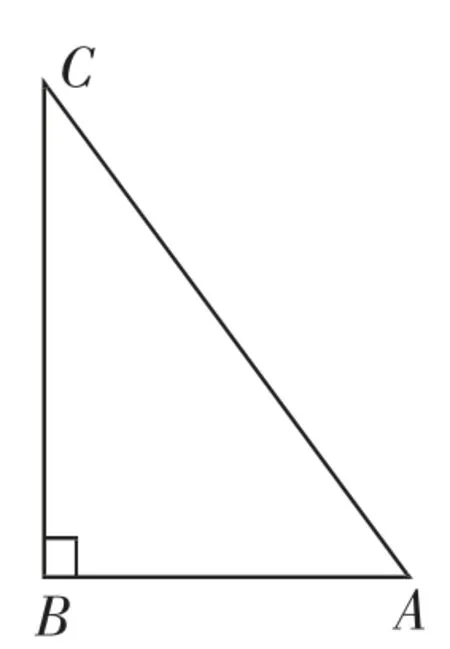
图1

图2

一题五解，让学生兴奋不已，深感数学的神奇魅力.兴奋之余，教师必须向学生指明这类问题的通法：

（1）矢量运算，根据向量运算的定义或是把向量转化为基底处理；

（2）坐标运算，通过建立合适的坐标系表示出题目中的点的坐标.坐标运算的思维要求相对较低，可优先考虑.

思考二、试卷评讲课要注重“一题多变”，培养学生思维的广阔性

我们倡导学生在“变”中学数学，试题评讲课更要注重“变”，即“一题多变”，通过对原考试题的结构变换，如数学情境的变化，已知条件的变化，已知条件与所求结论的互换等，让数学问题由浅入深，层层递进，这样不但可以上出试题评讲课的新意，吸引学生的注意力，而且还能收到触类旁通、举一反三的效果，培养学生思维的广阔性.

案例2求sin210°+cos240°+sin10°cos40°的值为______.

这是一道高一三角恒等变换单元的测试题目，属非特殊角三角函数求值问题，一般可通过“变角”变出特殊角，或通过改变式子结构，利用整体思想求值就可求得答案.本题也是一个“一题多解”的好素材，笔者先引导学生发现了三种解法（由于篇幅有限，这里略）后，又提出了以下变式，请大家思考：

变式1：求cos273°+cos247°+cos47°cos73°的值.

点拨：本题与原题相比，结构一脉相承，只是函数名做了变化，只要利用诱导公式就可将其还原，容易求得答案.

变式2：求sin2α+cos2（α+60°）+sinαcos（α+60°）的值.

点拨：本题结构依然与例题相同，但角加入了参数，容易发现两角之差是特殊角，这就是破解本题的突破口.受原题一题多解的启发，得到如下解答：

变式3：证明x+y=2kπ+（k∈Z），则sin2x+sin2y+sinxsiny 为定值

点拨：参照变式2，本题将结论一般化，具体如何证明可仿造变式2 的解答过程.（过程略）

值得说明的是，一题多变的目的是让学生感悟一类问题的解法，原题与变式之间，变式与变式之间的解法往往具有一致性，这样更有利于学生从一道题的讲解中掌握一类题的解法.

思考三、试卷评讲课要注重“一题多拓”，培养学生思维的深刻性

试卷评讲课，应该借助试题平台，引导学生开展研究性学习，让学生“温故而知新”.当一道试题分析完毕，教师应该将这个问题适当加以拓展，在题目的深度上做些思考，最常见而又最有效的教法就是“一题多拓”.即从学生的实际认知水平出发，通过对试题的开放性与发散性进行拓展，彰显问题的数学本质，通过对拓展问题的探究与探讨，进一步激活学生的思维，发展学生思维的深刻性.

案例3在△ABC 中，角A，B，C 所对的边分别为a，b，c，∠ABC=120°，∠ABC 的平分线交AC 于点D，且BD=1，则4a+c 的最小值为______.

本题出自2018年高考江苏卷，考查基本不等式的应用，难度中等偏上.高考结束后，笔者请高二学生也做了这份试题，发现此题的得分率并不理想，问题出在面对多元问题，学生不知如何去利用基本不等式.于是笔者在讲评课上，对此类多元不等式问题做了些拓展.

拓展1：若x，y，z 均为正实数，且x2+y2+z2=1，则的最小值为______.

拓展2：已知正数x，y 满足，那么y 的最大值为______.

拓展3：若实数x，y 满足2x2+xy-y2=1，则的最大值为______.

设计说明：拓展1 主要指导学生利用换元法将三元问题转化为一元问题；拓展2 可将两个变量分离，先将目标转化为求函数值域问题，再将其转化为解对应不等式问题，思维再上一个台阶.拓展3 是前2 题方法的综合，难度进一步加大，其解答如下：

把2x2+xy-y2=1 变为（x+y）（2x-y）=1，

从拓展3的解答可以看出，引进参数不是增加元，而是为了巧妙消元，引入一元参数t，消去两元x 与y，不仅使原式成为关于t 的函数，而且还可将其配成基本不等式应用的模式，真可谓“合理引参，巧夺天工”.将学生的思维推向更高的层次.

从某个角度看，讲评试卷是对考试的一种反思，而反思其实是一种更高层次的学习.因此教师讲评试卷，应引导学生思考，切不可就题论题，应借助“一题多解”、“一题多变”和“一题多拓”等手段，进一步激发学生的思维，为学生思维的可持续发展创造条件.