提升高中生数学运算素养的教学策略*
☉福建省德化第一中学 徐建新
在2017 年教育部颁发的《关于全面深化课程改革,落实立德树人根本任务的意见》中,各个学科都明确提出了具有学科特点的核心素养.《普通高中数学课程标准》(2017 年版)明确了六大数学核心素养,并对九个主题提出了具体的核心素养要求,其共同特点是都要求发展学生的逻辑推理和数学运算素养.其中,数学运算是指在明确运算对象的基础上,依据运算法则解决数学问题的素养,主要表现为:理解运算对象、掌握运算法则、探究运算思路、形成程序化思维.
笔者觉得,运算素养是在运算能力基础上提出的更高要求,应该包括运算能力、运算意识、运算品质、运算态度等.
从教学实践看,高中生数学运算存在以下几个常见问题:概念与法则理解不准确;公式、定理记错;思路不清,答题方向不明确;方法选择不恰当,运算烦琐;表达条理不清,上下行抄错等.针对上述问题,一方面,要注重培养学生运算时细致、耐心、韧劲、完美等优秀的数学品质;另一方面,即本文要阐述的在教学中提升高中生数学运算素养的策略问题.
一、“概念辨析”有利于“掌握运算法则”
核心概念要贯穿高中数学教学的始终.在概念教学中,通过符号变式、图形变式、语言变式等探究活动,辨析概念中的关键字眼,学生从不同角度对概念的内涵与外延获得更深刻的理解与认识.下面以“函数概念教学”为例.
判断下列对应关系是否是集合A 到B 上的函数.
(1)A={圆},B={x|x>0},对应关系f:对A 中的圆求周长与B 中的元素对应;
(2)A=R,B=R,对应关系f:对A 中的元素取倒数与集合B 中的元素对应;
(3)A={0,1},B={0,-1,1},对应关系f:对A 中的元素开平方与B 中的元素对应;
(4)A={0,-1,1},B={0,1},对应关系f:x→y=x2,x∈A,y∈B;
(5)A={0,1},B={0,1,2},对应关系f:x→y=x2,x∈A,y∈B.
分析:函数是特殊的映射,(1)集合A 不是数集,明确了函数的特殊所在.以上问题是针对“函数”的前提“A,B 是非空的数集”,以及定义中强调的“三性”:任意性、存在性、唯一性而设计的.
二、“公式推导”有利于“理解运算公式”
高中数学公式具有基础性、简洁性、科学性、重要性等特点.通过对公式的推导与证明,了解公式的产生、发展过程,以及公式使用的条件、适用范围等,有利于加深对运算公式的理解.以“基本不等式”为例.
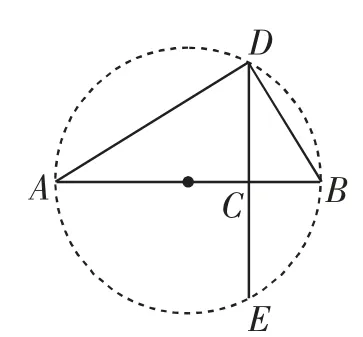
图1
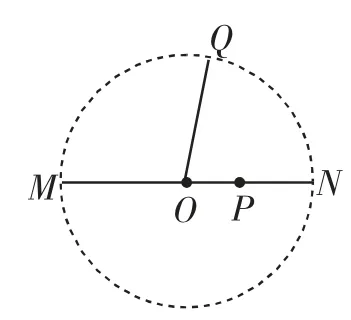
图2
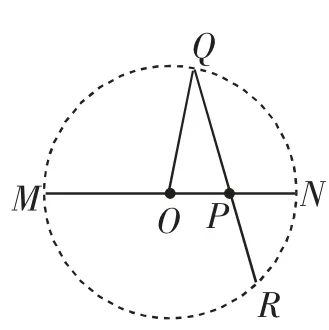
图3
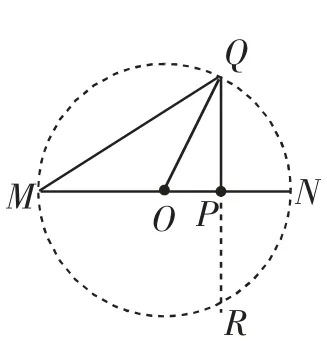
图4
如图2,作两条首尾转接的线段MP,PN,其长度分别是a,b,则
如图3,Q,P,R 三点画线,则PM·PN=PQ·PR=a·b;
三、“一题多解”有利于“选择运算方法”
“一题多解”是指用多角度看一道题,全面利用所学知识解决问题,既开拓学生视野、拓宽解题思路,又培养学生发散思维、提高灵活应用知识解决问题的能力.在探究“一题多解”的过程中,要关注考纲和学生学情,关注解法的选择.学生根据题意选择更加合理简洁的运算方法,体现了运算的灵活性和普适性.
四、“一题多变”有利于“理解运算对象”
“一题多变”,即“变式教学”,是数学教师较常用的教学方法之一.通过对已知条件、设问方式、求解目标等进行适当变式,有利于学生充分挖掘问题中已知与未知关系,理解运算对象的变化对运算方法与过程的影响.
五、“一般问题特殊化”有利于“运算的简洁性”
一般性问题往往涉及多个变量,不容易找到解决问题的突破口.“一般问题特殊化”就是取变量的特殊值、特殊位置、特殊结构等.比如,字母问题数字化、抽象函数具体化等.
其依据是:若命题在一般情况下正确,则在特殊情况下也正确;反之,若在特殊情况下该命题不正确,则在一般情况下也不正确的原理.它避开了复杂的逻辑推理、数学运算,使得求解过程更简洁,这个方法在选择题、填空题中应用广泛,也可以先探求结论,再证明结论的普遍性.
例1(2017 年新课标卷Ⅰ理11)设x、y、z 为正数,且2x=3y=5z,则( ).
A.2x<3y<5z B.5z<2x<3y
C.3y<5z<2x D.3y<2x<5z
分析:取x=1,则3y=3log32=log38<2,5z=5log52=log532>2.所以3y<2x<5z,故选D.
六、“特殊问题一般化”有利于“形成程序化思维”
“一般问题特殊化”应用广泛,特别是不需要运算过程、只需要求得结论的选择题和填空题.但对“特殊问题一般化”的方法不够重视.“特殊问题一般化”就是将问题放置于更加一般的情景中,得到普适性的结论与方法,再运用于特殊问题.一方面,提高对数学问题的本质认识;另一方面,一般化后的数学问题往往含多个字母,对提升数学运算素养大有益处.下面以双曲线的中点弦为例进行说明.
例2(人教A 选修2-1.P80.9)经过点M(2,1)作直线l 与双曲线交于A,B 两点,且M 为AB 的中点,求直线l 的方程.
分析:该问题的常用解法有三种,其中用“点差法”求斜率后写出方程最常用,其前提是所求直线的斜率是存在的.因此,需要将问题一般化,判断中点弦存在的条件.
一般化:经过点M(x0,y0)作直线l 与双曲线=1(a>0,b>0)交于A,B 两点,且M 为AB 的中点,求直线l 的方程.
这个求解过程是全字母运算,运算目标要明确,运算方向要清晰,运算过程要细心,心理活动要坚定,运算结果要合理(对称性).
七、“反思完善”有利于“运算的严谨性”
反思对于数学学习至关重要,对数学解题更是如此,不但要反思解题过程是否正确、完整,对存在的漏洞要进行修正补充,还要反思算理依据是否明确,在改变条件时,才不至于出错.以一道常见的函数极值问题为例.
例3已知函数f(x)=x3+ax2+bx+a2在x=1 处有极值为10,则a=______,b=______.
学生错解:
错因分析:当,时,f′(x)=3x2-6x+3=3(x-1)2≥0,函数f(x)在R 上单调递增,无极值点.正确答案只有
反思:若x=x0是函数f(x)的极值点,则f′(x0)=0;但f′(x0)=0 时,x0不一定是f(x)的极值点.

